Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 42401. |
Two equal metal bells are charged to 10 and -20 units of electricity. Then, they are brought in contact with each other and then again separated to original distance. The ratio of magnitude of force between the two balls before and after contact is : |
|
Answer» `8:1` |
|
| 42402. |
How much energy is required to separate the typical middle mass nucleus ._50^120Sn into its constituent nucleons. (Mass of ._50^120Sn =119.902199 u , mass of proton = 1.007825 u and mass of neutron = 1.008665 u) |
|
Answer» 1021 Mev |
|
| 42403. |
For sound waves, the Doppler formula for frequency shift differs slightly between the two situations: (i) source at rest, observer moving, and (ii) source moving, observer at rest. The exact Doppler formulas for the case of light waves in vacuum are, however, strictly identical for these situations. Explain why this should be so. Would you expect the formulas to be strictly identical for the two situations in case of light travelling in a medium? |
|
Answer» Solution :As sound waves are mechanical waves, they require some elastic MEDIUM (LIKE air) for their PROPAGATION. Among the two situations given in the statement, in the first situation, there is a relative motion between OBSERVER and medium whereas in the second situation, there is no relative motion between observer and medium. Hence these two situations are not identical. Hence, change in frequency of sound heard by listner (or noticed by observer), found out using Doppler.s formula is DIFFERENT in these two cases. In case of light waves, propagating in vacuum with the highest possible speed `c=3xx10^(8)m//s`, and relative motion between vacuum (or air) and observer becomes meaningless. Hence, Doppler.s formulae for light waves in the two situations (i) and (ii) (given in the statement) are indentical. If light waves are passing through any medium (other than air) then Doppler.s formulae are found to be different in the two situations, given in the statement. |
|
| 42404. |
The resolving power of a telescope depends upon the : |
|
Answer» FOCAL LENGTH of the OBJECTIVE |
|
| 42405. |
Two identical pendulums A and B are suspended from the same point. Both are given positive charge, with A having more charge than B. They diverge and reach equilibrium with the suspension of A and B making angles theta_(1) and theta_(2) with the vertical respectively. |
|
Answer» `theta_(1) gt theta_(2)` |
|
| 42406. |
Name the phenomenon due to which one cannot see through fog. |
| Answer» SOLUTION :SCATTERING of LIGHT | |
| 42407. |
Electric potential is given by v=6x-8xy^2 -8y+6yz-4z^2 then electric force acting on 2C point charge placed at origin will be |
| Answer» ANSWER :D | |
| 42408. |
The aperture of the largest telescope in the world is about 5 m. If the sepration between the moon and the earth is 4 xx 10^5km and the wavelength of visible light is 5000 A, then the minimum separation between the objects on the surface of the moon which can be just resolved is approximately equal to : |
|
Answer» 200 m |
|
| 42409. |
One mole of an ideal gas is contained in a perfectly insulating cylinder. Initially adiabatic piston of unit are and unit mass is in equilibrium. Now a block of same mass is kept gently on piston as shown in figure. (Take lambda=1.5,g=10m//s^(2) and neglect friction and assume change in temperature in whole gas is simultaneous) Depth upto which (piston+block) will move before coming to rest again is : |
|
Answer» `(sqrt(5)-1)/(2)m` `2mgh=(4)/(2)RDeltaT` `DeltaT=(10h)/(R )` …..(i) Initially, `(mg)/(A)(A.l)=RT_(1)` …(ii) and finally, `P_("max")A(l-h)=RT_(2)` …..(III) (iii)-(ii) `P_(m)(1-h)-10=10h` …..(iv) By equation of adiabatic PROCESS `PV=` constant `(mg)/(A)(Al)^(gamma)=P_("max"){A(l-h)}^(gamma)` `10=P_(m)(1-h)^(gamma)` Put this `P_(m)` in equation (iv) `10(1-h)^(1-gamma)-10=10h` `(1-h)^(1-gamma)-1=h` `(1-h)^(1-gamma)=(h+1)` `(1)/(sqrt(1-h))=(1+h)rArr(1)/((1-h))=(1+h)^(2)` `h(h^(2)+h-1)=0` `h=(sqrt(5)-1)/(2)m` and `P_(n)=(10)/((1-(sqrt(5)-1)/(2))^(3//2))=(20sqrt(2))/((3-sqrt(5))^(3//2))N//m^(2)` 
|
|
| 42410. |
If two waves are not coherent, then it obtained |
|
Answer» STEADY intereference |
|
| 42411. |
A rectangular block has dimensions 5 cm xx5 cm xx 10 cm. Calculate the resistance measured between (a) two square ends and (b) the opposite rectanglar ends specific resistance of the material is 3.5xx10^(-5) Omega m |
|
Answer» Solution :a) Resistance between two square ENDS `R_(1)=(rhol)/(A)rArr R_(1)=(3.5xx10^(-5)xx10xx10^(-2))/(5xx5xx10^(-4))` `=1.4xx10^(-3)Omega`  B) Resistance between the opposite rectangular ends `R_(2)=(rhol)/(A)rArr R_(2)=(3.5xx10^(-5)xx5xx10^(-2))/(5xx10xx10^(-4))=3.5xx10^(-4)Omega` |
|
| 42412. |
The frequencies of x-rays, y-rays and ultraviolet rays are respectively a, b and c. Then |
|
Answer» a < B, b > c |
|
| 42413. |
(A) : In micro wave oven the energy is not wasted in heating up the vessel. (R) : The principle of microwave oven is to generate microwave radiation with magnetron source of appropriate frequency in the work space of the oven where we keep food. |
|
Answer» Both 'A' and 'R' are TRUE and 'R' is the CORRECT EXPLANATION of 'A'. |
|
| 42414. |
It is known that 28 grams of a certain ideal gas occupy 22.4 liters at standard conditions (0°C, 1 atm). The volume occupied by 42 grams of this gas at standard conditions is |
|
Answer» 14.9 LITERS |
|
| 42415. |
There is a uniform electric field of intensity E which is as shown. How many labelled points have the same electric potential as the fully shaded point ? |
|
Answer» 2 |
|
| 42416. |
What is transducer? |
| Answer» SOLUTION : A device that CONVERTS ONE FORM of energy (SIGNAL) into another. | |
| 42417. |
A ball is dropped from a height of 20 cm. The ball rebounds to a height of 10 cm. What is loss of energy? |
| Answer» ANSWER :B | |
| 42418. |
Delta_(r)U^(@)of formation of CH_(4) (g) at certain temperature is - 393 kJ mol^(-1) .The value of Delta_(r)H^(@) is |
|
Answer» ZERO (s),(G),(g) `Deltan_(g)=-1` `DeltaH=DeltaU+Deltan_(g)RT` `Deltan_(g)=-ve` `DeltaHltDeltaU` |
|
| 42419. |
A rod of length L rotates about an axis passing through its centre and normal to its length with an angular velocity omega. If A is the cross section and D is the density of material of rod, its rotational K.E. is : |
|
Answer» `(1)/(2)AL^(3)DOMEGA^(2)` `=(1)/(2)Iomega^(2)=(1)/(2).(ML^(2))/(12).omega^(2)=(1)/(24)XX(ALD)L^(2)omega^(2)` `=(1)/(24)AL^(3)Domega^(2)` |
|
| 42420. |
A diverging lens with magnitude of focal length 25 cm is placed at a distance of 15 cm from a converging lens of magnitude of focal length 20 cm. A beam of parallel light falls on the diverging lens. The final image formed is ...... |
|
Answer» REAL and at a distance of 40 CM from the divergent LENS. 
|
|
| 42421. |
A dipole of electric dipole moment p is placed in a uniform electrie field of strength E. If theta is the angle between positive directions of p and E, then the potential energy of the electric dipole is largest when theta is |
|
Answer» `PI/4` |
|
| 42422. |
A centre zero galvanometer is connected in series with a switch and a battery . When the switch is closed and opened periodically (nearly about 4 times/sec) its needle |
|
Answer» reads always zero `thereforeI = (tau_n)/(n AB)=(18xx10^-5xx10^-2)/(60xx6xx10^-4xx500xx10^-4)` `=10^-3A` . |
|
| 42423. |
When two tuning forks A and B are sounded together, 4 beats per second are heard . The frequency of the fork B is 384 Hz. When one of the prongs of the fork A is filled and sounded with B the beat frequency increases, then the frequency of the work A is : |
|
Answer» Solution :`v_(A) = V_(B) pm 4 ` `v_(A)= 384 pm 4 = 380 Hz` or 388 Hz When the prongs of tunning fork A are FILED then frequency of tunning fork INCREASES and hence beat frequency will increase if `v_(A) ` = 388 Hz. So correct choice is (a). |
|
| 42424. |
Find the maximum intensity in case of interfarence of infinite identical coherent sources having intensities I_(0),(I_(0))/(4),(I_(0))/(16),(I_(0))/(64),(I_(0))/(256)…….. (upto infinite). |
|
Answer» `I_(0)` |
|
| 42425. |
In Fig. 6-54, a slab of mass m_(1) = 40 kg rests on a frictionless floor, and a block of mass m_(2) = 12 kg rests on top of the slab. Between block and slab, the coefficient of static friction is 0.60, and the coefficient of kinetic friction is 0.40. A horizontal force vecF of magnitude 120 N begins to pull directly on the block, as shown. In unit-vector notation, what are the resulting accelerations of (a) the block and (b) the slab? |
| Answer» SOLUTION :`(a)veca_(B)=-(6.1m//s^(2))HATI,(b)veca_(s)=-(1.2m//s)^(2)hati` | |
| 42426. |
If the amplitude of the magnetic field is 3 xx 10^(-6) T, then amplitude of the electric field for a electromagnetic waves is |
| Answer» Solution :`900 V m^(-1)` | |
| 42427. |
A sinusoidal voltage of peak value 285 V is applied to a series LCR circuit in which resistor of resistance 5 W, pure Inductor of Inductance 28.5 mH and capacitor of capacitance 800 mu R are connected. Find the resonant frequency. |
|
Answer» Solution :Given `V_("rms")= 285 V , R =5 Omega,L =28.5 mH=28.5xx10^(-3)H,C= 800mu F= 800xx10^(-6)`F a. Resonant FREQUENCY `gamma_(0)=(1)/(2pisqrt(LC))=(1)/(2xx3.14sqrt(28.5xx10^(-3)xx800xx10^(-6)))` `gamma_(0)=(1)/(2xx3.14sqrt(2.85xx10^(-2)xx800xx10^(-6)))=(1)/(6.28sqrt(2280xx10^(-6)))=(1)/(6.28xx47.74xx10^(-4))` `=(1)/(6.28xx47.74xx10^(-4))=(1)/(299.80xx10^(-4))=0.003335xx10^(4)=33.35` Hz b. Impedance , Z`= SQRT(R^(2)+(X_(L)-X_(e))^(2))` At resonance `X_(L) =X_(c)` `z=sqrt((5)^(2))` `Z= sqrt(25)` `Z = 5 Omega` `I_(rms) = (V_(rms))/(Z)= (285)/(5)` `I_(rms)= 57 A` Power dissipated at resonace `P=V_(rms)I_(rms)= 285xx57` `P = 16.245` watt |
|
| 42428. |
What is meant by transition temperature? |
| Answer» SOLUTION :The RESISTANCE of CERTAIN materials become zero below certain TEMPERATURE`T_(c )`. This temperature is known as critical temperature or transition temperature. | |
| 42429. |
A particle moving with a velocity equal to 0.4ms^(-1) is subjected to an acceleration of ms^(-2) for 2 seconds in a direction at right angles to the direction of motion. The magnitude of the final velocity is |
|
Answer» `0.3ms^(-1)` |
|
| 42430. |
Calculate the range of the variable capacitor that is to be used in a tuned-collector oscillator which has a fixed inductance of 150 pH.The frequency band is from 500 KHz to 1500KHz. |
|
Answer» Solution :Resonant frequency `f_(0) =1/(2PI sqrt(LC))` On simplifying we GET `C = 1/(4pi^(2)f_(0)^(2)L)` When frequency is equal to 500 kJz `C = 1/(4 xx 3.14^(2) xx (500 xx 10^(3))^(2) xx 150 xx 10^(-6)) = 676 pF` When frequency is equal to 1500 kHz `C = 1/(4 xx 3.14 xx (1500 xx 10^(3))^(2) xx 150 xx 10^(-6)) = 75 pF` Therefore, the capacitor range is 75 - 676 pF |
|
| 42431. |
Two balls of different masses are thrown in air with different velocities. While they are in air acceleration of centre of mass of the system. (neglect air resistance)? |
|
Answer» Depends on the DIRECTION of the MOTION of two balls |
|
| 42432. |
A coil is rotated in a uniform magnetic field about an axis perpendicular to the field. The emf induced in the coil would be maximum when the plane of coil is : |
|
Answer» PARALLEL to the FIELD |
|
| 42433. |
A glass rod rubbed with slik is broughtcloseto twounchargedmetallic spheres in contact with eachother,inducingchargeson themas shown in Fig. Describe what happens when (i) the spheresare slightly separated and (ii) the glass rod is subsequently removedandfinally (iii) the spheres are separated far apart. |
|
Answer» Solution :A glass road RUBBED with silk acquirespositivecharge. Whenthis rod is brought close to TWO uncharged metalllic spheres A and B in contact , negative chargeis inducedon the rightside of sphere B, Fig (i) When the spheresare SLIGHTLY separated , theinducedcharges are shownin Fig.(b). 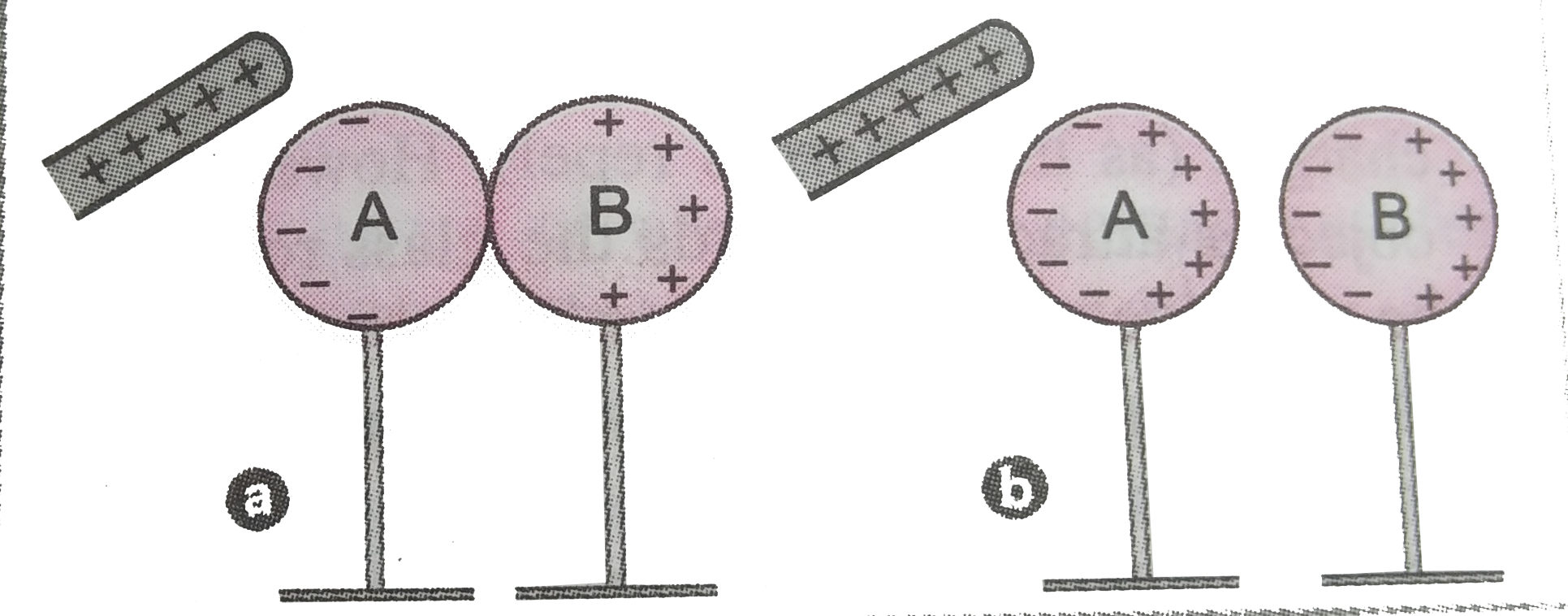 (II) As the glass rod is removedsubsequently and separation is too small, the DISTRIBUTION of charges on A and B remainsthe sameas shown in Fig. (iii) When A and B are placed at a largedistance , the positiveand negative chargeson each flow and neutralise, so thatno chargeis left on A or B. |
|
| 42434. |
If A 250V capacitors of C_(1)=2muF=2 xx 10^(-6)F""C_(2)=5muF=5 xx 10^(-6)F then find charge and energy stored in each capacitor. |
|
Answer» Solution :Data SUPPLIED, V=250V `C_(1)=2muF 2 XX 10^(-6)F ""C_(2)=5muF=5 xx 10^(-6)F` Charge in `C_(1), Q_(1)=C_(1) V=2 xx 10^(-6) xx250 =0.5 xx 10^(-3)C` Energy stored in `C_(1)=1/2 C_(1) V^(2)=1/2 xx 2 xx 10^(-6) xx (250)^(2)=0.0625 J` Charge in |
|
| 42435. |
Calculate the mass defect and the binding energy per nucleon of the ""_(47)^(108)Ag nucleus. [atomic mass of Ag = 107.905949] |
|
Answer» SOLUTION :MASS of proton, `m_(p) = 1.007825 amu` Mass of neutron, `m_(m) = 1.008665 amu` Mass defect, `Delta m = Zm_(p) + Zm_(N) - M_(N)` ` = 47 XX 1.007825 + 61 xx 1.00865 - 107.905949` ` = 108.89634 - 107.905949` `Delta m = 0.990391` u BINDING energy per nucleon of the `""_(47)^(108)"Ag"` NUCLEUS `overline(B.E) = (Delta m x 931)/(A) = (0.990391 xx 931)/(108)` ` = (922.05421)/(108) = 8.537` `overline(B.E) = 8.5 (MeV)/(A)` |
|
| 42436. |
In the given figure switch is open initially and capacitor C_2 is unchanged Energy in C1 is |
| Answer» Answer :D | |
| 42437. |
(a) Draw the schematic sketch of a cyclotron. Explain the shape of the path on which charged particle moves when the particle is accelerated by it. (b) To convert a given galvanometer into a voltmeter of ranges 2 V, V and V/2 volt, resistances R_(1),R_(2) and R_(3) ohm respectively, are required to be connected in series with the galvanometer. Obtain the relationship between R_(1), R_(2) and R_(3). |
|
Answer» After describing a semicircular path inside dee `D_(1)`, the particle comes in the gap between the two dees. In the resonance condition, the direction of electric field just gets reversed during this time and particle is again ACCELERATED towards the dee `D_(2)` and its velocity `v_(2)` becomes greater. So, the charged particle describes a semicircular path in dee `D_(2)` whose radius `r_(2)=(mv_(2))/(qB)` is slightly greater than `r_(1)` As time taken by charged particle to cover the semicircular path remains unchanged, same thing happens again and again and particle describes semicircular paths of gradually increasing radii in dees `D_(1)` and `D_(2)` again and again. 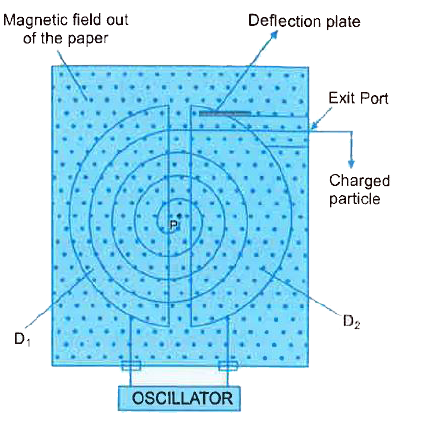 (b) Let us have a GALVANOMETER of resistance `R_(G)` and giving full scale deflection for a current `I_(g)` to CONVERT it into a voltmeter of ranges 2V,V and `V/2` respectively, we are JOINING resistances `R_(1),R_(2)` and `R_(3)` so we have `R_(1)=(2V)/(I_(g))-R_(g)` ...(i) `R_(2)=V/(I_(g))-R_(g)`....(ii) and `R_(3)=(v//2)/(I_(g))-R_(g)` ....(iii) On solving these equations, we get `R_(1)-R_(2)=2R_(3)` or `R_(1)=R_(2)+2R_(3)` |
|
| 42438. |
Referring to the previous illustration (a) Where do the particles meet? (b) What are the speeds of the particles at the time of meeting? |
|
Answer» SOLUTION :(a)`s_(1)=(1//2)GT^(2)=(1//2)(10)(3)^(2)=45m`from the top (b)`v_(1)=gt_(1)=10xx3=30m//sec` `v_(2)=10-10xx(3-2)=0` |
|
| 42439. |
Explain the principle on which the working of a potentiometer is based. Why is the use of a potentiometer preferred over that of a voltmeter for measurement of emf of a cell ? |
Answer» SOLUTION : A potentiometer works on the principle that for a constant current flowing through the potentiometer WIRE of uniform cross-section, the fall in potential is directly proportional to length. Let as shown in ADJOINING FIG., a battery of emf `epsi_0` is connected across a potentiometer wire of length L and resistance R and an external series resistance R.. Then constant current flowing through the potentiometer wire is `I = (epsi_0)/((R + R.))` `therefore `Fall in potential along the potentiometer wire ` = IR = (epsi_0 R)/((R+ R.))` and the fall in potential per unit length (i.e., the potential gradient) `k = (epsi_0 R)/((R + R.)L.) ` ,which is a constant. Thus, potential drop across a length l of potentiometer wire V = kl, which is the basic working principle of the potentiometer. For measurement of emf of a cell, a potentiometer is preferred over a VOLTMETER because at the time of taking the reading no current is being drawn from the given cell and the cell is in an open circuit. |
|
| 42440. |
Hydraulic press is based upon |
|
Answer» ARCHIMEDE's principle |
|
| 42441. |
A spherically symmetric charge distribution is characterized by a charge density having the following variation :rho (r ) = rho_0 (1 - r/R) for r lt R rho (r ) = 0for r ge R. Where r is the distance from the centre of the charge distribution and rho_0 is a constant. The electric field at an internal point (r lt R) is |
|
Answer» `(rho_0)/(in_0) (r/3 - (r^2)/(4R))` |
|
| 42442. |
Draw the circuit diagram of a metre bridge to explain how it is based on Wheatstone bridge. |
Answer» Solution :Circuit diagram of a METRE BRIDGE is shown here, which clearly SHOWS that it based on Wheatstone.s bridge. 
|
|
| 42443. |
The potential differnce between the terminals of a battery of emf 6.0 V and internal resistance 1 Omega drops to 5.8 V when connected across an external resistor . Find the resistance of the external res |
|
Answer» |
|
| 42444. |
Assertion: Coloured spectrum is see when we look at a distant light source through a fine muslin cloth. Reason: It is due to the diffraction of white light on passing through fine slits present between the threads of muslin cloth. |
| Answer» SOLUTION :Reason GIVES correct EXPLANATION of assertion. | |
| 42445. |
Select the correct output Y |
|
Answer» `A.B` |
|
| 42446. |
The number of electrons emitted by a surface exposed to light is directly proportional to |
|
Answer» FREQUENCY of light |
|
| 42447. |
A bar magnet of magnetic moment M_1 is suspended by a wirein a magnetic field. The tip of the wire is rotated through180^(@) , then the magnet rotated through45^(@) . Under similar conditions the magnet of magnetic moment M_2 is rotated through30^@ . Then find the ratio of M_2& M_2. |
|
Answer» Solution :We knowthat TORQUE `, tau = MB sin theta ` But ` tau = C phi` . `:. C phi = MB sin theta ` For FIRST magnet , ` C xx 180= M_1B sin 45^(@)` ....... (1) For second magnet , ` C xx 180 = M_2B sin30^(@)` ....... (2) From eqs. (1) and (2) `M_1 B sin 45^(@) = M_2 B sin 30^(@) implies (M_1)/(M_2) = (sin 30^@)/(sin 45^(@))` `implies (M_1)/(M_2) = (1//2)/(1 // sqrt(2)) = (sqrt(2))/(2) = (1)/(sqrt(2))` `:. M _1 : M_2 = 1: sqrt(2)` |
|
| 42448. |
Which of the following dimensions represent current density ? |
|
Answer» `M^0L^-2T^0A` |
|
| 42449. |
In the given figure net magnetic field at O will be |
|
Answer» `(2mu_(0)i)/(3pi a) sqrt(4-PI^(2))`  Magnetic FIELD at 0 due to Part(1) : `B_(1)= 0` Part(2): `B_(2) = (mu_(0))/(4pi).(pi i)/((a//2)) ox` (along-Z-axis) Part(3) `B_(3) = (mu_(0))/(4pi) .(i)/((a//2))(darr)` (along-Y-axis) Part (4): `B_(4) = (mu_(0))/(4pi).(pi i)/((3a//2)) o.` (along +Z-axis) Part (5): `B_(5) =(mu_(0))/(4pi).(i )/((3a//2))(darr)` (along-Y-axis) (along-Z-axis) `B_(3) + B_(5) = (mu_(0))/(4pi).(1)/(a) (2 + (2)/(3))= (8mu_(0)i)/(12pi a) (darr)` (along-Y-axis) Hence net magnetic field `B_("net") = sqrt((B_(2)- B_(4))^(2) +(B_(3)+ B_(5))^(2)) = (mu_(0)i)/(3pi a) sqrt(pi^(2) + 4)` |
|
| 42450. |
In U - V method, the object distance is 30.0cm and image distance is 60.0cm from pole of concave mirror. The percentage error in measurement of focal length of mirror is (n)/(18)%. Find the value of n |
| Answer» ANSWER :A | |