Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 38051. |
gamma represents the ratio of two specific heats of a gas. For a given mass of the gas, the change in internal energy when the volume expands from V to 3V to constant pressure P is |
|
Answer» `(3PV)/((gamma - 1))` But `C_(V) = (R )/((gamma - 1)) :. Delta U = (nR Delta T)/((gamma - 1))` According to the ideal gas EQUATION, PV = nRT At constant pressure, `Pdelta V = nR Delta T` `:. Delta U = (PDelta V)/((gamma - 1)) = (P(3V - V))/((gamma- 1)) = (2PV)/((gamma - 1))` |
|
| 38052. |
In damped oscillatory motion a block of mass 200g is suspended to a spring of force constant 90 N//m in a medium and damping constant is 40g//s. Find time taken for its amplitude of oscillation to drop to half of its initial value |
|
Answer» Solution :Mass ,= 200G= 0.2 kg force constant k = `90N//m` damping constant `b = 40g//s =0.04 kg//s`. `sqrt(km)= sqrt(90 xx 0.2)= sqrt(18) kg//s` Here `b lt lt sqrt(km)` amplitude = `Ae^(-bt//2m)` Let amplitude is dropped to half of its initial value after the time `T_(1//2)`: Amplitude `Ae^((-bT_(1//2))/(2m))= (A)/(2) implies e^((-bt_(1//2))/(2m))= (1)/(2)` Take NATURAL logarithms on both sides `(-bT_(1//2))/(2m)= "LN"((1)/(2))implies T_(1//2)= ("ln"(2))/(b//2m)= 2.302 xx 0.3010xx2m//b` `T_(1//2)= 0.693 xx(2m)/(b)= 0.693xx (2 xx 0.2)/(0.04)= 6.93s` |
|
| 38053. |
A stone is thrown vertically from the ground. It reaches the maximum height of 500 m in 10 sec. After what time it will reach the ground from the maximum height reached? |
|
Answer» 5s |
|
| 38054. |
In damped oscillatory motion a block of mass 200g is suspended to a spring of force constant 90 N//m in a medium and damping constant is 40g//s. Find time period of oscillation |
|
Answer» Solution :MASS ,= 200g= 0.2 kg force constant K = `90N//m` damping constant `b = 40g//s =0.04 kg//s`. `sqrt(km)= sqrt(90 xx 0.2)= sqrt(18) kg//s` Here `b lt lt sqrt(km)` TIME period `T= 2pisqrt((m)/(k))= 2pisqrt((0.2)/(90))= 0.3s` |
|
| 38055. |
A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical A small block kept in the bowl rotates with the bowl without slipping on its surface If the surface of bowl is smooth and angle made by radius through the block with the vertical is 0 find the angular speed at which the bowl is rotating . |
|
Answer» Solution :Here ` OA = R, ANGLEAOC = theta` Block moves in a horizontal circle with centre`C` and radius` r = AC = R sin theta` `:.` In equilibrium `N cos theta = MG` and `N sin theta = m OMEGA^(2) (R sin theta)` `N = m omega^(2) R` From(i)`m omega^(2) R cos theta = mg` ` omega = sqrt((g)/(R cos theta))` 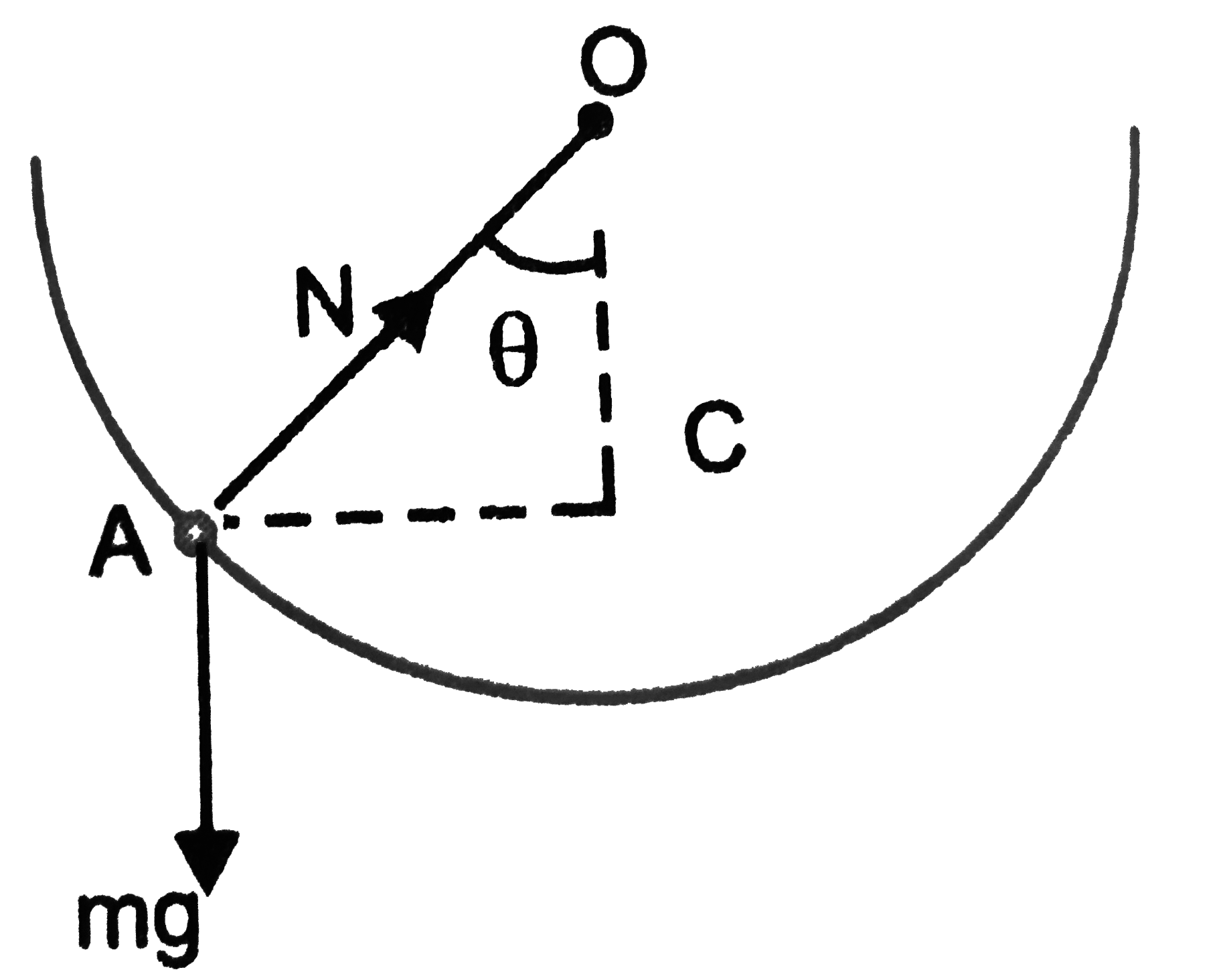 . .
|
|
| 38056. |
From a tower of height H, a particle is thrown verticially upward with a speed u. The time taken by the particle to hit the ground is n times that taken by it to reach the highest point of its path. The relation between H, u and n is |
|
Answer» 2gH=`n^(2)u^(2)` Speed on reaching the ground = `sqrt(u^(2)+2gh)` Now,V = u+at or, `sqrt(u^(2)+2gh)=-u+"GT"` or, `t= (u+sqrt(u^(2)+2gH))/(g)` According to the EQUESTION, ` (u+sqrt(u^(2)+2gH))/(g)=("nu")/(g)` or, `2gH=n(n-2)u^(2)` 
|
|
| 38057. |
In the Atwood's machine the system starts from rest. What is the speed and distance moved by each mass at t = 3s? |
|
Answer» |
|
| 38058. |
For bodies of regular shape and uniform mass distribution, the center of mass is at |
|
Answer» the corners |
|
| 38059. |
6.7 gm of water at 50^@C be divided in two parts such that when one part of mass .x. gm is turned into ice at 0^@C , it would release sufficient amount of heat to vaporize the other part . The (x-0.49) gm is equal to ___ gm |
|
Answer» |
|
| 38060. |
If I_(1)I_(2), and I_(3) are moments of inertia of a disc about its geometric axis, diameter and a tangent in its plane, then |
|
Answer» `I_(1)GT I_(2)gt I_(3)` |
|
| 38061. |
The radii of two soap bubbles are R_1and R_2 respectively the ratio of masses of air in them will be |
|
Answer» <P>`(R_(1)^(3))/( R_(2)^(3))` |
|
| 38062. |
If the diameter of the earth becomes half its present value but its average density remains unchanged then how would the weight of an object on the surface of the earth be affected? |
|
Answer» Solution :G = `GM/R^2` = `G/R^2 4/3 piR^3rho` = `4/3 piGR RHO` g = `4/3 piG (R/2) rho` = g/2 . Hence the weight of the OBJECT will be HALVED. |
|
| 38063. |
If the linear density of a rod of length L varies as lambda=(kx^(2))/(L) where k is a constant and x is the distance of any point from one end, then find the distance of centre of mass from the end at x=0. |
Answer» Solution :Let the x-axis be along the length of the rod and origin at one of its ends. As rod is along x-axis, for all points on it y and z co-ordinates are zero.  Centre of mass will be on the rod. Now consider an element of rod of length dx at a distance x from the origin, then `DM=lambda` dx`=(KX^(2))/(L)dx` so, `X_(CM)=(int_(0)^(L)xdm)/(int_(0)^(L)dm)=(int_(0)^(L)x(kx^(2))/(L)dx)/(int_(0)^(L)(kx^(2))/(L)dx)=(int_(0)^(L)x^(3)dx)/(int_(0)^(L)x^(2)dx)=((L^(4))/(4))/((L^(3))/(3))=(3L)/(4)` |
|
| 38064. |
When a disc rotates with unform angular velocity, which of the following is not true ? |
|
Answer» The sense of ROTATION remains same |
|
| 38065. |
An ideal gas undergoes a quasistatic, reversible process in which its molar heat capacity C remains constant. It during this process the relation the pressure p and volume V is given by pV^n=constant, then n is given by (here C_p and C_v are molar specific heat at constant pressure and constant volume respectively). |
|
Answer» `n=C_p/C_v` For 1 mol of ideal gas `pV=RT`……..(2) Dividing (1) by (2) we get `V^(n-1) T=k/R` `THEREFORE((dV)/(dT))=V/((n-1)T)=V/((1-n)T)` According to first law of THERMODYNAMICS `dQ=C_vdT+pdV` `therefore(dQ)/(dT)=C_V+p((dV)/(dT))=C_v+(pV)/((1-n)T)=C_v+R/(1-n)` Hence thermal capacity, `C=C_v+R/(1-n)` or,`1-n=R/(C-C_v)` or,`n=1-R/(C-C_v)=(C-(C_v-R))/(C-V_v)=(C-C_p)/(C-C_v)`[`because C_p-C_v=R`] |
|
| 38066. |
A bucket filled with water weighing 20 kg is raised from a well of depth 20m. If the lineat density of the rope is 0.2 kg per meter, the amount of work done is, (g=10 ms^(-2)) |
| Answer» Answer :C | |
| 38067. |
A light particle moving horizontally with a speed of 12 m/s strikes a very heavy block moving in the same direction at 10 m/s. The collision is one dimensional and elastic. After the collision, the particle will be |
|
Answer» move at 2 m/s in its ORIGINAL direction LET `v_1` be velocity of the light particle after COLLISION. `v_1 = ((m_1 -m_2)u_1)/(m_1 + m_2) + (2m_2 u_2)/(m_1 + m_2) "" ……..(i)` Given : `m_1 < < m_2` So, `m_1` can be ignored compared to `m_2`. From equation (i) we get , `v_1 = - u_1 + 2u_2` Substituting the VALUES , we get `v_1 = -12 m//s + 2(10 m//s) = 8 m//s` in its original direction. |
|
| 38068. |
In the figure, a smooth pulley of negligible weight is suspended by a spring balance. Weights of 1 kg and 5kg are attached to the opposite ends of a string passing over the pulley and move with an acceleration due of gravity. During their motion, the spring balance reads a weight of |
|
Answer» 6 kg |
|
| 38069. |
The fire fighters attach brass jets at the end of water pipes. Why? |
| Answer» SOLUTION :To Increase the VELOCITY of water issuing out of the nozzle as the area a of the TIP is very SMALL, increases in agreement with the equation of continuity ay a constant | |
| 38070. |
For a progressive wave, y = 5 sin (0.01 x - 2t) (where x and y are in cm and t is in s). What will be its speed od propagation ? |
|
Answer» SOLUTION :Comparing `y =5 sin (0.01x -2t)` with ` y = A sin (kx - omega t )` We get `k =0.01 rad//cm, omega =2 rad//s` Now, WAVE VELOCITY is `V = (omega )/(k) = (2)/(0.01) =200 cm//s` |
|
| 38071. |
The force exerted by the floor of an elevator on the foot of a person standing there is more than the weight of the person if the elevator is (a) going up and slowing down(b) going up and speeding up(c ) going down and slowing down(d) going down and speeding up |
|
Answer» B and C are CORRECT |
|
| 38072. |
Certain volume of a liquid is taken in a Jong glass tube and its temperature is increased at a uniform rate, the rate of increase in the length of the liquid depends on (a) length of the liquid coloumn (b) area of cross section of the glass tube (c) coefficient of expansion of glass |
|
Answer» only (a) is CORRECT |
|
| 38073. |
A uniform wire of length 6.28 cm is bent in the form of a circle. The shift in its centre of mass is |
| Answer» ANSWER :A | |
| 38074. |
The amount of heat energy required to raise the temperature of 1 g of helium at NTP, from T_(1)K to T_(2)K is |
|
Answer» `(3)/(2)N_(a)k_(B)(T_(2)-T_(1))` |
|
| 38075. |
Optical fibers are based on |
| Answer» Answer :(a) | |
| 38076. |
The displacement of a particle is given by y (t) =2t ^(2) +5m.Hence its velocity at the end of 6 sec. will be ...... m/s. |
|
Answer» 77 `v = 4T` `therefore t = 6 SEC.` speed `therefore v = 4 xx 6 = 24m//s` |
|
| 38077. |
A metallic sphere of mass M falls through glycerine with a terminal velocity v. If we drop a ball of mass 8M of same metal into a column of glycerine, the terminal velocity of ball will be |
|
Answer» 2V `therefore R^(3)=8r^(3)` or `R=2R` As `v prop r^(2)` `therefore (v')/(v)=((R)/(r))^(2)=((2r)/(r))^(2)=4` or `v'=4v` |
|
| 38078. |
Which of the following properties are suitable for a cooking utensil ? |
|
Answer» HIGH specificheat |
|
| 38079. |
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is |
|
Answer» `(rg)/(sqrt(L^(2)-R^(2)))` |
|
| 38080. |
A sphere is rolling down on a sufficiently rough inclined surface. |
|
Answer» Direction of friction is up the plane |
|
| 38081. |
A tuning fork is used to produce resonance in a glass tube . The length of the air column in this tube can be adjusled by a varlable pision. At room temperature of 27^(@) C, two successlve resonances are produced at20 cm and 73 cm of column length .If the frequency of the tuning fork is 320 Hz, the velocity of sound in air at 27^(@) C is |
|
Answer» 350 m/s `(2 n + 1) (lambda)/(4) = 73` Subtracting EQUATION (2) from equation (1) . We get `(2 n + 1 - 2 n + 1) (lambda)/(4) = (73 - 20)` or,`(lambda)/(2) = 53 or, lambda = 106 cm = (106)/(100) m` `:. (V) = nlambda = 320 xx (106)/(100) = 339 . 2 m//2` |
|
| 38082. |
Smooth block is released at rest on a 45^@incline and then slides a distance d. If the time taken of slide on rough incline is n times as large as that to slide than on a smooth incline. Show that coefficient of friction. mu = (1- (1)/(n^2)) |
|
Answer» Solution :When there is no friction, the block slides down the inclined plane with ACCELERATION. ` a = g SIN theta ` when there is friction, the downward acceleration of the block is ` a. =g (sin theta - mu COS theta)` As the block slides a distance d in each case so ` d = 1/2 at^2 = 1/2 a.t.^2` `(a)/(a.) = (t.^2)/(t^2) = ((nt)^2)/(t^2) = n^2 " or"(g sin theta)/(g (sin theta -mu cos theta) )=n^2` Solving , we get (using ` theta =45^@` ) `mu = 1 - (1)/(n^2)` |
|
| 38083. |
A ball of mass 'm' approaches a wall of mass 'M' (gt gtm) with speed 4m/s along the normal to the wall. The speed of wall is 1m/s towards the ball. The speed of the ball after an elastic collision with the wall is |
|
Answer» 5m/s AWAY from the wall |
|
| 38084. |
Intensity of gravitational field inside the hollow spherical shell is |
|
Answer» VARIABLE |
|
| 38085. |
In the question number 36, at which distance a weight may be hung along the rod, in order to produce equal strains in both the wires? |
|
Answer» `(4)/(3)m`from steel wire For equal strain in both the wire, `(T_(S))/(A_(S)Y_(S)) = (T_(B))/(A_(B)Y_(B))` `therefore (T_(S))/(T_(B))=(A_(S))/(A_(B)) (Y_(S))/(Y_(B)) = (0.1 cm^(2))/(0.2 cm^(2)) xx (2xx 10^(11)N m^(-2))/(1 xx 10^(11) N m^(-2))= 1 .......(i)` For therotational equlibrium of the rod, `T_(S)x = T_(B) (2-x)` `(2-x)/(x) = (T_(S))/(T_(B))= 1""["Using (i)"]` `2 - x = x or x=1m ` |
|
| 38086. |
If you place your hands on a wooden and a metal chair at the same temperature,lower than your body temperature, which of them do you find hotter? |
| Answer» SOLUTION :The WOODEN CHAIR. | |
| 38087. |
Let the speed of the planet at the perihelion P be V_pand the sun-planet distance SP be r_p Relates (r_p,V_P )to the corresponding quantities at the aphelion (r_(A),V_A)Will the planet take equal times to tranverse BAC and CPB ? |
Answer» Solution : According to LAW of CONSERVATION of angular MOMENTUM. Angular momentum of the planet at P = Angular momentum of the planet at A `implies mV_pr_(p) = mV_(A)r_(A) " (or) " V_p/V_A=r_(p)/r_(p)` Since `r_A gt r_p` so `V_p gt V_A` Here area SBAC is greater than the area SCPB. According to Kepler.s second law, as areal velocity of the planet , is constant around the sun. i.e. equal areas areas are swept on equal times, hence the planet will take longer time to traverse BAC then CPB. |
|
| 38088. |
4.0 g of a gas occupies 22.4 litres at NTP. The specific heat capacity of the gas at constant volume is 5.0 "JK"^(-1) "mol"^(-1). If the speed of sound in this gas at NTP is 952 "ms"^(-1) , then the heat capacity at constant pressure is _____ (R=8.3 "JK"^(1) "mol"^(-1)) |
|
Answer» `8.5 "JK"^(-1) "MOL"^(-1)` `v=sqrt((gammaRT)/M)` `therefore gamma=(mv^2)/(RT)` `=(4xx10^(-3)xx(952)^2)/(8.3xx273)` `=3625.2/2265.9` `therefore gamma=1.599` `therefore gamma approx` 1.6 `therefore` The HEAT capacity at constant pressure , `C_P=gammaC_V=1.6xx5.0=8.0 "JK"^(1) "mol"^(-1)` |
|
| 38089. |
What are the conditions necessary for a satellite to appear stationary. |
|
Answer» Solution :`implies ` The conditions NECESSARY for a satellite to appear stationary are : 1)Satellite having the circular orbit is in the equatorial plane of the earth. 2) Its ORBITAL time period of revolution is 24 hours. 3)The satellite must TRAVEL eastward (WEST - east) at the same rotation speed as the earth. 4) It should be at a height nearly 36000 km above the equator of earth. The inclination of the orbit must be ZERO. |
|
| 38090. |
The sciences which deal with …….. Are called physical sciences. |
|
Answer» |
|
| 38091. |
A man swims from a point A on the bank of a river if width 100 m. When he swims perpendicular to the water current, he reaches the other bank 50 m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is. . |
|
Answer» `10^@` upstream `tan THETA = (v_w)/(v_m) = (50)/(100) = (1)/(2) or v_m = 2v_w` Refer to (Fig .S5.68) (B), `sin prop = (v_w)/(v_m) = (v_w)/(2 v_w) = (1)/(2)` or `theta = 30^@` So, it is `60^@` upstream. (a)  , ,
|
|
| 38092. |
A block of mass m resting on a smooth horizontal plane starts moving due to a constant force F=mg//3 of constantmagnitude. In the process of its rectilinear motion the angle theta varies as theta=lamdas, where lamda is constant and s is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle theta. Also show that the block will never lose contact with the ground. |
Answer» Solution :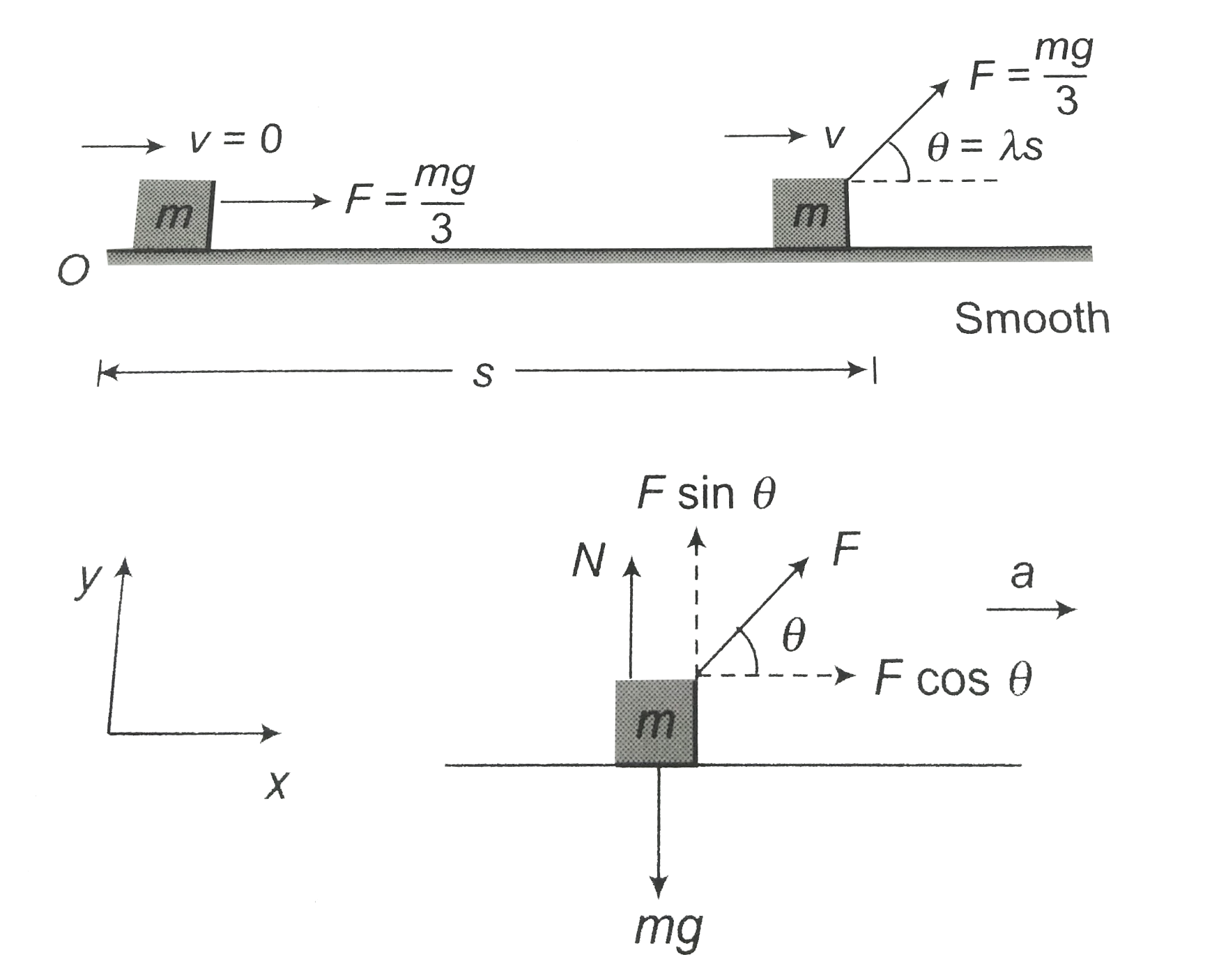 `x-`direction`:` `Fcostheta=ma` `a=(F)/(m)costheta=(mgcos(lamdas))/(3m)` `v(dv)/(dx)=(g)/(3)COS(lamdas)` `int_(0)^(v)vdv=(8)/(3)int_(0)^(s)cos(lamdas)ds` `|(v^(2))/(2)|_(0)^(v)=(g)/(3)(|sin(lamdas)|_(0)^(s))/(lamda)` `v^(2)=(2g)/(3lamda)sin(lamdas)` `v=sqrt(2gsintheta)/(3lamda)` `y-`direction`:` `N+Fsintheta=mg` `N=mg-(mg)/(3)sintheta` `(sintheta)_(max)=1,N_(MIN)=(2mg)/(3)` Since normal reaction will NEVER will never be zero and hence the block will never LOSE constact with the ground. |
|
| 38093. |
A ball strikes an identical ball with velocity 50 m/s and after the collision which is perfectly elastic it is found to move with velocity 30 m/s . Show that the two balls move at right angles to each other after collision . |
| Answer» | |
| 38095. |
A light inextensible smooth string is in contact with a smooth-pulley (fixed at C) through an anglephis shown in figure. If T is the tension in the string, then force with which the string presses the pulley vertically is xTsin ( phi//2)then x is. |
|
Answer» |
|
| 38096. |
Pick out the dimensionless quantity……….. |
| Answer» Solution :specific gravity | |
| 38097. |
An accelration produces a narrow beam of protons, each having an initial speed of v_(0). The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. If the initial kinetic energy of a proton is 2.56 ke V, then the final potential of the sphere is |
|
Answer» `2.56 kV` `rArr 3/4xx2.56=1.92 kV` |
|
| 38098. |
(A) : The velocity of a body at the bottom of an inclined plane of given height, is more when it slides down the plane, compared to when it rolling down the same plane. (R ) : In rolling down a body acquires both kinetic energy of translation and rotation |
|
Answer» Both 'A' and 'R' and true and 'R' is the correct EXPLANTATION of 'A' |
|
| 38099. |
An accelration produces a narrow beam of protons, each having an initial speed of v_(0). The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. The limiting electric potential of the sphere is |
|
Answer» `(3m_(P)v_(0)^(2))/(8e)` `(KE)_(i)=1/2 mv_(0)^(2): (KE)_(F)=1/2 m(v_(0)/2)^(2)` `:.` Electric potential `=(3mv_(0)^(2))/(8e)` |
|
| 38100. |
If the radius of the earth becomes half of its present value but its density remains unchanged then find the weight of body on the surface of earth. |
|
Answer» Solution :`implies g =(GM_(e))/R_e^2=G/(R_e^2)(4/3piR_e^3rho)=4/3 piR_erho` Since the RADIUS becomes HALF, `g. = 4/3 piG((R_e)/2)rho =1/2 (4/3 pi GR_erho)` `:. g. =g/2 ` soweight becomes half Weight `W PROP g` `:. (W.)/W = (g.)/g` `:. W. = W XX 1/2` ` :. W. = W/2` |
|