1.

A block of mass m resting on a smooth horizontal plane starts moving due to a constant force F=mg//3 of constantmagnitude. In the process of its rectilinear motion the angle theta varies as theta=lamdas, where lamda is constant and s is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle theta. Also show that the block will never lose contact with the ground.

Answer» <html><body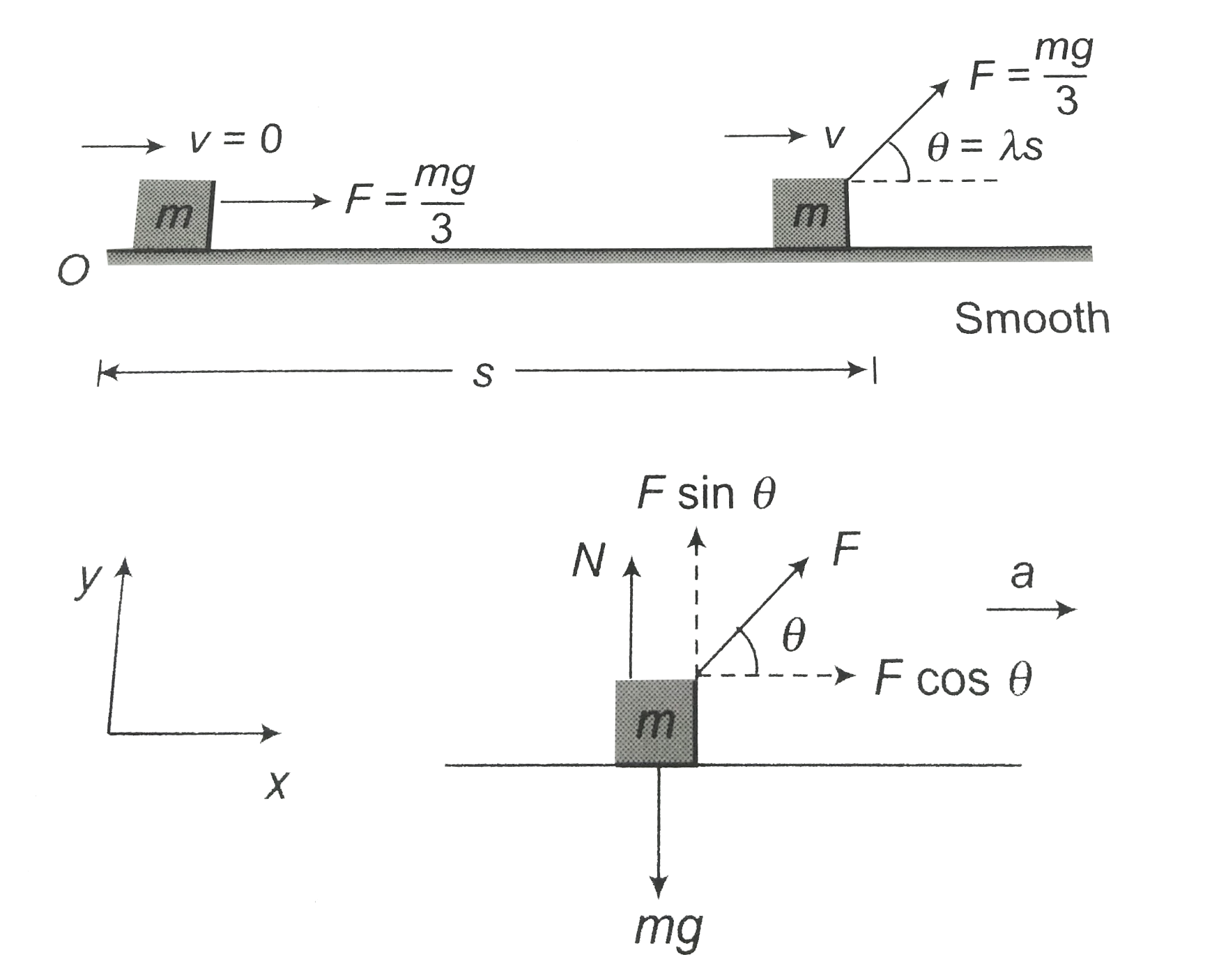><p></p>Solution :<img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V01_C06_S01_046_S01.png" width="80%"/> <br/> `x-`direction`:` `Fcostheta=ma` <br/> `a=(F)/(m)costheta=(mgcos(lamdas))/(3m)` <br/> `v(dv)/(dx)=(g)/(3)<a href="https://interviewquestions.tuteehub.com/tag/cos-935872" style="font-weight:bold;" target="_blank" title="Click to know more about COS">COS</a>(lamdas)` <br/> `int_(0)^(v)vdv=(<a href="https://interviewquestions.tuteehub.com/tag/8-336412" style="font-weight:bold;" target="_blank" title="Click to know more about 8">8</a>)/(3)int_(0)^(s)cos(lamdas)ds` <br/> `|(v^(2))/(2)|_(0)^(v)=(g)/(3)(|sin(lamdas)|_(0)^(s))/(lamda)` <br/> `v^(2)=(2g)/(3lamda)sin(lamdas)` <br/> `v=sqrt(2gsintheta)/(3lamda)` <br/> `y-`direction`:` `N+Fsintheta=mg` <br/> `N=mg-(mg)/(3)sintheta` <br/> `(sintheta)_(max)=1,N_(<a href="https://interviewquestions.tuteehub.com/tag/min-548008" style="font-weight:bold;" target="_blank" title="Click to know more about MIN">MIN</a>)=(2mg)/(3)` <br/> Since normal reaction will <a href="https://interviewquestions.tuteehub.com/tag/never-570518" style="font-weight:bold;" target="_blank" title="Click to know more about NEVER">NEVER</a> will never be zero and hence the block will never <a href="https://interviewquestions.tuteehub.com/tag/lose-537625" style="font-weight:bold;" target="_blank" title="Click to know more about LOSE">LOSE</a> constact with the ground.</body></html>


Discussion

No Comment Found

Related InterviewSolutions