Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 38101. |
Two bodies of masses 10 kg and 20 kg are located in X-y plane at (0, 1) and (1,0). The position of their centre of mass is |
|
Answer» (2/3, 1/3) |
|
| 38102. |
On an open ground , a motorist follows a track that turns to his left by an angle of 60^(@) after every 500 m. Starting from a giventurn , specify the displacement ofof themotorist at thethird , sixth and eighth turn . Compare the magnitude of the displacement with the total path length covered by the motorist in each case. |
| Answer» Solution :Displacement of magnitude 1 km and direction `60^(@)` with theinitial direction , totalpath length = 1.5km (third turn), NULL displacement VECTOR , path length = 3 km (sixth turn), 866 `m.30^(@)`, 4 km (eight turn) | |
| 38103. |
A small glass marble of mass 'm' oscillates between the two edges, inside a hemispherical glass bowl of radius 'r'. If 'V' is the speed of marble at the lowest position, the normal reaction at that position is |
|
Answer» `(mv^2)/(R )` |
|
| 38104. |
A 4g bullet is fired horizontally with a speed of 300 m/s into 0.8kg block of wood at rest on a table and gets embedded in the block. If the coefficient of friction between the block and the table is 0.3, how far will the block slide approximately ? |
|
Answer» 0.19 m |
|
| 38105. |
Time (T), velocity (C) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be: |
|
Answer» `[M]=[T^(-1) C^2h]` |
|
| 38106. |
Which of the following relations is not correct ? |
|
Answer» `1 A.U = 1.496xx 10^(11)m` |
|
| 38107. |
A body freely falling from a height h describes (11h)/(36) in the last second of its fall. The height h is (g=10ms^(-2)) |
|
Answer» 125m |
|
| 38108. |
Find antilog of (i) - 2.6674 (ii) - 3.01 (iii) -0.3467 |
|
Answer» Taking antilog on both the sides, we GETX = 0.002151 (II) Given, log `x = - 3.01 = bar 4 + 4 - 3.01 = bar 4.99` Taking antilog on both the sides, we GET x = 0.0009772 (iii) Given log `x = - 03467 = bar 1 + 1 -0.3467 = bar1. 6533` Taking antilog on both the sides, we get x = 0.4501 |
|
| 38109. |
Describe the moment of a force about a point as a vector quantity. |
|
Answer» Solution :In Fig. O is the POINT of rotation, P is the point of application of a force `vecF`, `vecr`=`vecOP`, POSITION vector of the point `vecP`, with respect to the point O. Then the moment of the force `vecF` about the point O, is `vecF=vecrxxvecF` According to the PROPERTIES of cross PRODUCT the direction of the vector `vecG` is along the direction of advance of a righthanded screw, when it is rotated from `vecr` towards `vecF`. The direction of `vecG`, as shown in the figure, is perpendicular to the plane of rotation, i.e., ALWAYS along the axis of rotation. 
|
|
| 38110. |
An accelration produces a narrow beam of protons, each having an initial speed of v_(0). The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. One the potential of the sphere has reached its final, constant value, the minimum speed v of a proton along its trajectory path is given by |
|
Answer» `v_(0)` `mv_(0)xxR/2=mvxxRrArr v=V_(0)/2` |
|
| 38111. |
What is 'retrograde motion' of planets? |
| Answer» Solution :When the motion of the planets are observed in the night SKY by NAKED EYES over a period of a few months, it can be seen that the planets move eastwards and REVERSE their motion for a while and return to eastward motion again. This is CALLED 'retrograde motion' of planets. | |
| 38112. |
An accelration produces a narrow beam of protons, each having an initial speed of v_(0). The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as |
|
Answer» 1 |
|
| 38113. |
Find the height to which the water rise when a capillary tube of radius 0.24 mm is dipped vertically in a beaker containing water. Surface tension of water is 7.0xx10^(-2)Nm^(-1), angle of contact is 0^(@) and density of water is 1000Kgm^(-3). |
|
Answer» |
|
| 38114. |
An accelration produces a narrow beam of protons, each having an initial speed of v_(0). The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. The total energy (E) of a proton in the beam travelling with seed v at a distance of r (r ge R) from point O. Assuming that the sphere has acquired an electrostatic charge Q is |
|
Answer» `(EQ)/(4piepsilon_(0)r)` HENCE total ENERGY is greater than `(eQ)/(4pi in_(0)r)` |
|
| 38115. |
Show that for a simple pendulum, the work done by the tension of the string becomes zero during its oscillation. |
| Answer» Solution :Work done by a force is the productof the force with the component of the displacement of THEDISPLACEMENT along the force. In the CASE of an OSCILLATING siple pendulum, tension in the bob. HENCE, the component of displacement of the bob is zero in the direction of tension, therefore, the tension does notdo anywork. | |
| 38116. |
What is meant by the term potential energy ? Give its two examples. |
| Answer» Solution :The energy POSSESSED by the body by VIRTUE of its position is called POTENTIAL energy. | |
| 38117. |
If a bullet is suddenly stopped the rise in temperature is independent of |
|
Answer» MASS of the BULLET |
|
| 38118. |
(A) : Law of conservation of momentum is the consequence of Newtons third law. (R ) : Action, Reaction pairs are internal forces in collisions. |
|
Answer» Both (A) and (R ) are TRUE and (R ) is the CORRECT explanation of (A) |
|
| 38119. |
Moment of inertia of a circular ring about a given axis is…………..moment of inertia of…………of………….and………………about the same axis. |
| Answer» SOLUTION :GREATER than , CIRCULAR DISC , same mass , same SIZE. | |
| 38120. |
Particle A is moving with a constant velocity of V_(A) = 50 ms^(–1) in positive x direction. It crossed the origin at time t = 10 s. Another particle B started at t = 0 from the origin and moved with a uniform acceleration of a_(B) = 2 ms^( –2) in positive x direction. (a) For how long was A ahead of B during the subsequent journey? (b) Draw the position (x) time (t) graph for the two particles and mark the interval for which A was ahead of B. |
|
Answer» `(##IJA_PHY_V01_C02_E01_057_A01##)` |
|
| 38121. |
A thin rectangular strip ABCD of thickness d is such that the coefficient of linear expansion ' alpha' of any section of the strip (of the form XY) distant 'x' from the face AB varies as alpha= alpha_(0) + alpha_(1) x. Determine the radius of curvature of the strip when heated through a temperature range Delta T |
|
Answer» `( 1)/( 2 alpha_(1) ( Delta T) ) [2 + ( alpha_(0) + alpha_(1) d) Delta T)` |
|
| 38122. |
The Ratio of the escape velocity to the orbital velocity of a surface satellite of the earth is |
|
Answer» `SQRT2` |
|
| 38123. |
A 2kg block is dropped from a height of 0.4 m on a spring of force constant 1960Nm^(-1). The maximum compression of the spring is |
| Answer» ANSWER :C | |
| 38124. |
Non -viscous flow can be a streamline. |
|
Answer» `THEREFORE` From `R_(e)=(rhovD)/(eta),R_(e)` = infinite HENCE , such type of flow can never be a STREAMLINE. |
|
| 38125. |
A splash is heard 3.12s after a stone is dropped into a well 45 m deep. The speed of sound in air is [g=10ms^(-2)] |
|
Answer» `330ms^(-1)` |
|
| 38126. |
Derive the expression for the terminal velocity of a sphere moving in a high viscous fluid using stokes force. |
|
Answer» Solution :Expression for terminal velocity : Consider a sphere of radius R which falls freely through a highly viscous liquid of COEFFICIENT of viscosity `eta`. Let the density of the material of the sphere be `RHO` and the density of the fluid be `sigma`. Gravitational force acting on the sphere. `F_(G) = mg = (4)/(3)pi r^(3)rho g` (downward force) Up thrust, `U = (4)/(3)pi r^(3) sigma g` (upward force) viscous force `F= 6pi eta r v_(t)` At terminal velocity `v_(t)` downward force = upward force `F_(G) - U = F rArr (4)/(3) pi r^(3) rho g - (4)/(3) pi r^(3) sigma g = 6pi eta r v_(t)` `v_(t) = (2)/(9) xx (r^(2)(rho - sigma))/(eta) g rArr v_(t) PROP r^(2)` Here, it should be noted that the terminal speed of the sphere is directly proportional to the square of its radius. If `sigma` is greater than `rho`, then the term `(rho - sigma)` becomes negative leading to a negative terminal velocity. 
|
|
| 38127. |
What is the efficiency of time realisation in cesium atomic clocks ? |
|
Answer» Solution :The UNCERTAINTY in time REALISATION of a CESIUM ATOMIC clock is `+- 10^(-13).` it implies that such CLOCKS gain or loss no more then ` 3mu s` in one year. |
|
| 38128. |
A particle moves with position vector given by r=3t^(2)hat(i)+4hat(j) where r is measured in metres and t in seconds. For t gt0. Match the entries in Column I with those in Column - II. {:("Column-I","Column-II"),("(A) Angular acceleration","(P) increase with time"),("(about the axis passing through the origin)",),("(B) Liner momentum of the particle ","(Q) decrease with time"),("(C) Angular speed of the particle about the axis passing through the origin","(R) constant in time"),("(D) Magnitude of angular momentum of the particle with respect the origin is ","(S) directly proportional to the time."),(,"(T) is along negative axis "):} |
|
Answer» |
|
| 38129. |
The simple harmonic motion of a particle is governed by x = A sin (omega t + phi) where phi = (5pi)/6 Find the position and direction of movement of particle at t=0 a) |
|
Answer» A/2, NEGATIVE X-AXIS |
|
| 38130. |
Which of the following velocity-time graphs shows a realistic situation for a body in motion |
|
Answer»
|
|
| 38131. |
Two discs have the same mass and thickness. Their materials are of densities d_(1) and d_(2). The ratio of their M.I about their central axis is |
|
Answer» `d_(2):d_(1)` |
|
| 38132. |
A block of wood is floating on water at 0^(@)C with a certain volume 'V' above the water level. The temperature of water is slowly raised to 20^(@)C . How does the volume 'V' change with the rise in temperature ? |
|
Answer» remain unchanged |
|
| 38133. |
Let us assume that our galaxy consists of 2.5 x× 10^(11) stars each of one solar mass. How long will a star at a distance of 50,000 ly from the galactic centre take to complete one revolution? Take the diameter of the Milky Way to be 10^(5) ly. |
| Answer» SOLUTION :`3.54 ×x 10^(8)` YEARS. | |
| 38134. |
A Carnot engine will sink temperature at 17^(@)C has 50% efficiency. By now much should its source temperature by changed to increase its efficiency to 60% ? |
|
Answer» 225 K INITIALLY, `(50)/(100) = 1 - (273 + 17)/(T_(1))` or `(290)/(T_(1)) = (1)/(2)` or `T_(1) = 580 K` Finally, `(60)/(100) = 1 - (273 + 17)/(T._(1))` or `(290)/(T._(1)) = (2)/(5)` or `T._(1) = 725 K` `:.` Change in source TEMPERATURE `= (725 - 580) K = 145 K` |
|
| 38135. |
A liquid of specific heat 0.5 cal/g^(0)c at 60^(0)C, is mixed with another liquid of specific heat 0.3 cal/gm^(0)c at 20^(0)C. After mixing, the temperature of the mixture becomes 30^(0)C. In what proportion by weight are the liquids mixed ? |
|
Answer» `1:2` |
|
| 38136. |
Two parallel glass plates separated by a very short distance l, contains and oil drop of volume V, introduced between them. If theta be the angle of contact and T the surface tension of the oil, find the force with one presses against the other. |
|
Answer» |
|
| 38137. |
Two needles are floating on the surface of water. A hot needle when touches water surface between the needles, then they move |
|
Answer» closer |
|
| 38138. |
A body of mass 0.40 kg moving initially with a constant speed of 10 m s^(-1) to the north is subject to a constant force of 8.0 N directed towards the south for 30 s.Take the instant the force is applied to bet = 0, the position of the body at that time to be x = 0, and predict its position att = –5 s, 25 s, 100 s. |
|
Answer» Solution :u = `10 ms^(-1)` m= 0.40kg (Northdirection) t=30 s Herenorthdirectionis consideredas POSITIVEAND southdirectionisconsideredas negative Forceis appliedfor t=30 s  (i) At t=5 sposition `X_(1) = ut` `=10xx (-5)` (ii)at t=25 s `x_(2)ut + (1)/(2)4r^(2)` where`a = (F )/( m ) =(-8)/(0.4)= - 20ms^(-2)` `=250- 6250` `-=6 km` when forceis appliedfor 30s distancecovered velocityof objectafter30 s = u+ 9t =10 -600 (III)Positionof objectat t=100s `:.x_(100)= x_(30) a + x_(70)` =-870041300 `=-5000 m` `=-50 km` Thuspositionat -5 s 25 s and 10 willbe-50 m-6 kmand-50 km |
|
| 38139. |
A block of mass 20 kg is placed on a rough horizontal plane and a horizontal force of 12 N is applied. If coefficient of friction is 0.1 the frictional force acting on it is, |
| Answer» Answer :B | |
| 38140. |
The dimensional formula of the physical quantity whose S.I. unit is farad is |
|
Answer» `ML^(2)T^(-3)I^(-2)` |
|
| 38141. |
A closed hollow insulated cylinder is filled with gas 0°C and also contains an insulated piston of negligible weight and negligible thickness at the middle point. The gas on one side of the piston is heated to 100°C. If the piston moves 5cm, the length of the hollow cylinder is |
|
Answer» 13.65 cm |
|
| 38142. |
A bullet of mass 25g moving with a velocity of 500 ms^(-1) enters into a wooden block and comes out of it with a velocity of 100 ms^(-10. Find the work done by the bullet while passing through the wooden block. |
|
Answer» Solution :`m= 25 XX 10^(-3) kg, u= 500m//s, v= 100m//s` Work energy theorem `W= (1)/(2) mv^(2)- (1)/(2) m u^(2)` `=(1)/(2) xx 25 xx 10^(-3) [(100)^(2)- (500)^(2)]= 300J` |
|
| 38143. |
A ball is thrown straight up . What is its velocity and acceleration at the top ? |
| Answer» Solution :Atthe highest POINT, the VELOCITY of the ball is zero and its accelertion is equal to ACCELERATION due to gravity ACTING is DOWNWARD direction. | |
| 38144. |
In the following which is not the unit of time |
|
Answer» LEAP year |
|
| 38145. |
Can the coefficent of frictionbe more than one |
| Answer» Solution :Yes. The COEFFICIENT of friction can be more than one in some cases such as silicone rubber. Coefficient of friction is the ratio of FRICTIONAL force to NORMAL force. i.e., `F = mu R` . If `mu`is greater than one means frictional force is greater than normal force. But in general case the VALUE is usually between 0 and 1. | |
| 38147. |
A ball is dropped from a height h on a floor if the coefficient of restitution ise. Find the (a). Speed of ball after the first second … n^(th) collision. (b). Maximum height attained by the ball, after the first, second … n^(th) collision. (c). Time taken by the ball to reach the highest point after the first, second, ...n^(th) collision. (d). total distance covered by the ball. (e). totol time of journey. |
Answer» Solution :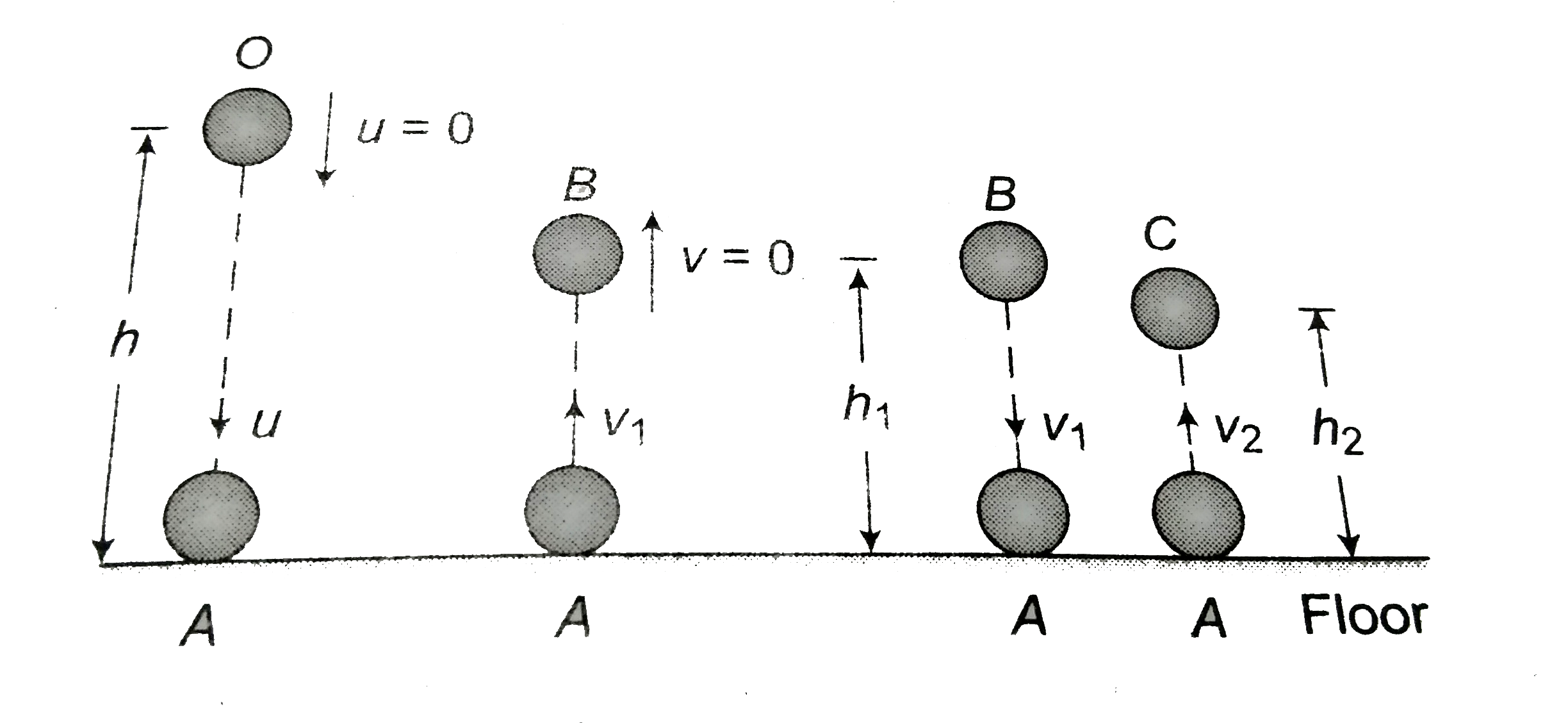 O to A: Speed of the ball when it hits the ground `u=sqrt(2gh)` Time take by the ball to hit the floor, `h=(1)/(2)g t_(0^(2))impliest_(0)=sqrt((2h)/(g))` `v_(1)-v_(2)=-e(u_(1)-u_(2))` 1 ball, 2 floor `u_(2)=v_(2)=0` `v_(1)=-eu_(1)=-EU` Speed of the ball after the FIRST collision `=eu` A to B `0=v_(1)^(2)-2gh_(1)impliesh_(1)=(v_(1)^(2))/(2g)=(e^(2)u^(2))/(2g)=(e^(2)xx2gh)/(2g)=e^(2)h` HEIGHT attained by the ball after the first collision `=e^(2)h` `0=v_(1)-g t_(1)impliest_(1)=(v_(1))/(g)=(eu)/(g)=(e)/(g)sqrt(2gh)=esqrt((2h)/(g))=et_(0)` After every collision the speed becomes e times. Maximum height becomes `e^(2)` times. time to reach at the heighest point becomes e times. `{:(,1^(st)"collision","After 2nd collision",n^(th)" collsion"),("speed of ball",eu,e^(2)u,e^(n)u),("Maximum height",e^(2)h,e^(4)h,e^(2n)h),("Time to reach at highest point",et_(0),et_(0),e^(n)t_(0)):}` when `u=sqrt(2gh),t_(0)=sqrt(2h//g)` TOTAL distance covered by the ball `S=h+2h_(1)+2h_(2)+. . . infty` `=h+2e^(2)h+2e^(4)h+. . . infty` `=h+2e^(2)h{1+e^(2)+. . .infty}` `=h+2e^(2)h{(1)/(1-e^(2))}=((1+e^(2))/(1-e^(2)))h` Total time of journey `T=t_(0)+2t_(1)+2t_(2)+... infty` `=t_(0)+2et_(0)+2e^(2)t_(0)+. . . infty` `=t_(0)+2et_(0)(1+e+ . . .infty)` `=t_(0)+2et_(0)((1)/(1--e))=((1+e)/(1-e))t_(0)=((1+e)/(1-e))sqrt((2h)/(g))` |
|
| 38148. |
A satellite is revolving in a circular orbit round the earth at a height of h. If the acceleration due to gravity at theta height is g. The orbital speed of the satellite. |
|
Answer» `SQRT(gh)` |
|
| 38149. |
Let bar(upsilon), upsilon_("rms") and upsilon_(p) respectively denote the mean speed, root mean square speed and most probable speed of the molecules in an ideal monatomic gas at absolute temperature T. The mass of a molecule is m. Then: |
|
Answer» No MOLECULE can have a SPEED GREATER than `sqrt(2) upsilon_("rms")` |
|
| 38150. |
Eiffel tower is made up of iron and its height is roughly 300 m. During winter season (January) in France the temperature is 2^(@)C and in hot summer its average temperature 25^(@)C. Calculate the change in height of Eiffel tower between summer and winter. The linear thermal expansion coefficient for iron alpha = 10xx10^(-6)" per "^(@)C |
|
Answer» Solution :`(DeltaL)/(L) = alpha_L DeltaT = DeltaL = alpha_L L DeltaT` `DeltaT = 10 xx 10^(-6) xx 300xx23 =0.69 m = 69 CM` |
|



