1.

A ball is dropped from a height h on a floor if the coefficient of restitution ise. Find the (a). Speed of ball after the first second … n^(th) collision. (b). Maximum height attained by the ball, after the first, second … n^(th) collision. (c). Time taken by the ball to reach the highest point after the first, second, ...n^(th) collision. (d). total distance covered by the ball. (e). totol time of journey.

Answer» <html><body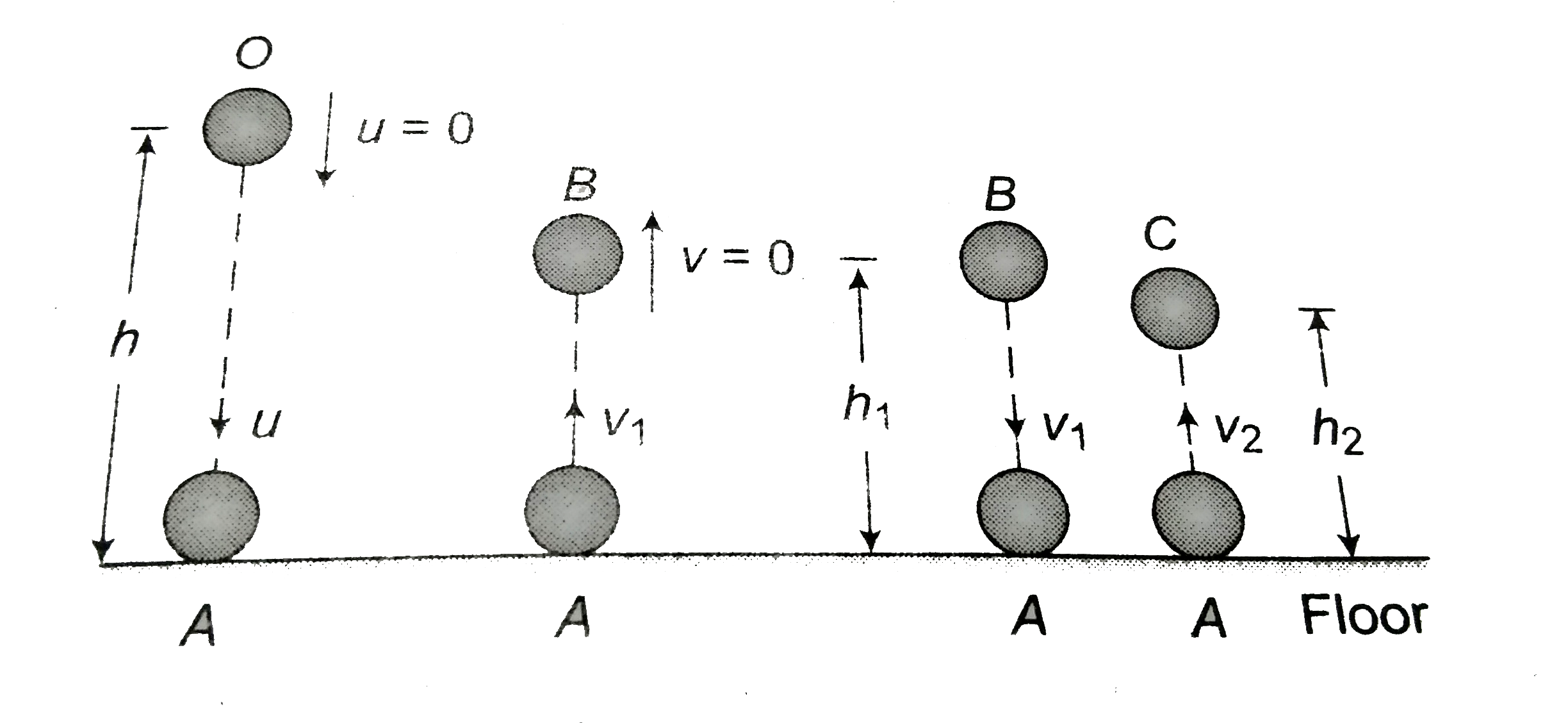><p></p>Solution :<img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V01_C10_S01_151_S01.png" width="80%"/> <br/> O to A: <br/> Speed of the ball when it hits the ground `u=sqrt(2gh)` <br/> Time take by the ball to hit the floor, <br/> `h=(1)/(2)g t_(<a href="https://interviewquestions.tuteehub.com/tag/0-251616" style="font-weight:bold;" target="_blank" title="Click to know more about 0">0</a>^(2))impliest_(0)=sqrt((2h)/(g))` <br/> `v_(1)-v_(2)=-e(u_(1)-u_(2))` <br/> 1 ball, 2 floor <br/> `u_(2)=v_(2)=0` <br/> `v_(1)=-eu_(1)=-<a href="https://interviewquestions.tuteehub.com/tag/eu-446864" style="font-weight:bold;" target="_blank" title="Click to know more about EU">EU</a>` <br/> Speed of the ball after the <a href="https://interviewquestions.tuteehub.com/tag/first-461760" style="font-weight:bold;" target="_blank" title="Click to know more about FIRST">FIRST</a> collision `=eu` <br/> A to B <br/> `0=v_(1)^(2)-2gh_(1)impliesh_(1)=(v_(1)^(2))/(2g)=(e^(2)u^(2))/(2g)=(e^(2)xx2gh)/(2g)=e^(2)h` <br/> <a href="https://interviewquestions.tuteehub.com/tag/height-1017806" style="font-weight:bold;" target="_blank" title="Click to know more about HEIGHT">HEIGHT</a> attained by the ball after the first collision `=e^(2)h` <br/> `0=v_(1)-g t_(1)impliest_(1)=(v_(1))/(g)=(eu)/(g)=(e)/(g)sqrt(2gh)=esqrt((2h)/(g))=et_(0)` <br/> After every collision the speed becomes e times. Maximum height becomes `e^(2)` times. time to reach at the heighest point becomes e times. <br/> `{:(,1^(st)"collision","After 2nd collision",n^(th)" collsion"),("speed of ball",eu,e^(2)u,e^(n)u),("Maximum height",e^(2)h,e^(4)h,e^(2n)h),("Time to reach at highest point",et_(0),et_(0),e^(n)t_(0)):}` <br/> when `u=sqrt(2gh),t_(0)=sqrt(2h//g)` <br/> <a href="https://interviewquestions.tuteehub.com/tag/total-711110" style="font-weight:bold;" target="_blank" title="Click to know more about TOTAL">TOTAL</a> distance covered by the ball <br/> `S=h+2h_(1)+2h_(2)+. . . infty` <br/> `=h+2e^(2)h+2e^(4)h+. . . infty` <br/> `=h+2e^(2)h{1+e^(2)+. . .infty}` <br/> `=h+2e^(2)h{(1)/(1-e^(2))}=((1+e^(2))/(1-e^(2)))h` <br/> Total time of journey <br/> `T=t_(0)+2t_(1)+2t_(2)+... infty` <br/> `=t_(0)+2et_(0)+2e^(2)t_(0)+. . . infty` <br/> `=t_(0)+2et_(0)(1+e+ . . .infty)` <br/> `=t_(0)+2et_(0)((1)/(1--e))=((1+e)/(1-e))t_(0)=((1+e)/(1-e))sqrt((2h)/(g))`</body></html>


Discussion

No Comment Found

Related InterviewSolutions