Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 38201. |
Gravel is dropped on a conveyor belt at the rate of 2 kg/s. The extra force required to keep the belt moving at 3ms^(-1) is |
| Answer» ANSWER :D | |
| 38202. |
A particle moves in the x-y plane with a constnat acceleration of 1.5m//s^(2) in the direction making an angle of 37^(@) with the x-axis. At t=0 the particle is a the origin and its velocity is 8.0 m/s along the x-axis. Find the velocity and the position of the particle at t=4.0s. |
|
Answer» |
|
| 38203. |
A machine rated as 150 W, changes the velocity of a 10 kg mass from 4 ms^(-1)" and "10 ms^(-1) in 4s. The efficiency of the machine nearly is |
| Answer» ANSWER :A | |
| 38204. |
IF infty_0 and mu_0 are respectively, the electric permitivity and the magnetic permeability of free space in and mu the corresponding quantities in a medium, then the refractive index of the medium is |
|
Answer» `SQRT(MU in)/(mu_0 in_0)` |
|
| 38205. |
Four rods A, B, C and D of the same length and material but of different radii r, r sqrt(2),r sqrt(3) and 2r respectively are held between two rigid walls. The temperature of all rods is increased through the same range. If the rods donot bend, then a) The stress in the rods A, B, C and D are in the ratio 1:2:3:4 b) The forces on them exerted by the wall are in the ratio 1:2:3:4 c) The energy stored in the rods are due to elasticity are in the ratio 1:2:3:4 d) The strains produced in the rods are in the ratio 1:2:3:4 |
|
Answer» only a |
|
| 38206. |
Calculate the speed of sound in a steel rod whose Young's modulus Y = 2 xx 10^(11) N m^(-2) and rho = 7800 kg m^(-3) |
|
Answer» Solution :`V = SQRT((Y)/(rho)) = sqrt((2 xx 10^(11))/(7800)) = sqrt(0.2564 xx 10^(8)) = 0.506 xx 10^(4) ms^(-1) = 5 xx 10^(3) ms^(-1)` Therefore , longitudinal waves travel faster in a solid than in a LIQUID or a gas . Now you may understand why a SHEPHERD checks before crossing railway track by keeping his ears on the rails to SAFEGUARD his cattle . |
|
| 38207. |
When a load of 80N is suspended from a string, its length is 101mm. If a load of 100N is suspended , its length is 102mm. If a load of 160N is suspended from it, then length of the string is (Assume the area of cross-section unchanged) |
|
Answer» 15.5 CM |
|
| 38208. |
A particle is moving in a circle of radius r under the action of a force F= alpha r^(2) which is directed towards centre of the circle. Total mechanical energy (kinetic energy + potential energy) of the particle is (take potential energy =0 for r= 0) : |
|
Answer» `(1)/(2) alpha r^(3)` |
|
| 38209. |
Water drops fall from the roof of a building 20 m high at regular time intervals. If the first drop strikes the floor when the sixth drop begins to fall, the heights of the second and fourth drops from the ground at that instant (g=10ms^(-2)) |
|
Answer» 12.8m and 3.2m |
|
| 38210. |
The unit of reduction factor of tangent galvanometer |
|
Answer» Ampere |
|
| 38211. |
What is meant by Frame of reference? |
| Answer» SOLUTION :If a coordinate system and the position of an OBJECT are described RELATIVE to it . Then such a coordinate system is CALLED FRAME of reference. | |
| 38212. |
A body of mass 2 kg begins to slide down a plane inclined at an angle of 45^@ with the horizontal. The force of friction will be |
|
Answer» 13.9 N |
|
| 38213. |
1 liter dry air at STP expands adiabatically to a volume of 3L. If gamma=1.4, the work done by air is (3^(1.4)= 4.655) (Take air to be an ideal gas) |
|
Answer» 18J After adiabatic expansion, `P_(2)=? And V_(2)= 3L` For adiabatic expansion `P_(1)V_(1)^(gamma) = P_(2) V_(2)^(gamma)` [ `:.T` is constant] `:. P_(2) = P_(1) ((V_(1))/(V_(2)))^(gamma)` `=1 ((1)/(3))^(gamma)` `=((1)/(3))^(1.4) [ :. gamma= 1.4]` `= (1)/(3^(1.4))= (1)/(4.655)` = 0.2148 atm WORK done in adiabatic process, `W= (P_(1)V_(1)- P_(2)V_(2))/(gamma-1)` `=(1 xx 1-0.2148 xx 3)/(1.4-1)` `=(1-0.6444)/(0.4)` `=(0.3556)/(0.4)` `W= 0.889 xx 1.01 xx 10^(5) xx 10^(-3)J` 91 atm = `1.01 xx 10^(5) (N)/(m^(2)) 1L= 10^(-3) m^(3)`] `:. W= 0.89789xx 10^(2)J` `:. W= 89.789J` `:. W= 90J` |
|
| 38214. |
Two bodies start moving in the same straight line at the same instant of time from the same origin. The first body moves with a constant velocity of 40m//s, and the second starts from rest with a constant acceleration of 4m//s^(2). Find the time that elapses before the second catches the first body. Find also the greatest distance between then prior to it and the time at which this occurs. |
|
Answer» Solution :When the SECOND body catches the first, the DISTANCE travelled by each is the same. `therefore 40T=(1)/(2)(4)t^(2)ort=20S` Now, the distance s between the two bodies at any time t is `s=ut-(1)/(2)at^(2)` For s to be maximum, `(ds)/(dt)=0oru-at=0` or `t=(u)/(a)=(40)/(4)=10S` Maximum Distance `=40xx10-(1)/(2)xx4xx(10)^(2)=400-200=200m` |
|
| 38215. |
A body of mass 1.0 kg strikes elastically with another body at rest and continues to move in the same direction with one-fourth of its initial velocity. The mass of the other body is |
|
Answer» 0.6 kg  According to the law of convervation of LINEAR MOMENTUM , we get `m_1 u_1 + m_2 xx 0 = m_1 v_1 + m_2v_2` or `m_1 u_1 = m_1 xx (u_1)/(4) + m_2v_2 " or " m_2v_2 = 3/4 m_1u_1 ""….(i)` According to the law of conservation of kinetic energy, we get `1/2 m_1 u_1^2 + 1/2 m_2 xx 0^2 = 1/2 m_1v_1^2 + 1/2 m_2v_2^2` or `m_2v_2^2 = 15/16 m_1u_1^2 "".....(ii)` Divide (ii) by (i), we get `(m_2 v_2^2)/(m_2v_2) = (15/16 m_1 u_1^2)/(3/4 m_1 u_1) " or " v_2 = 5/4 u_1` On substituting this value of `v_2` in (i), we get `m_2 5/4 u_1 = 3/4 m_1 u_1 " or " m_2 = 3/5 m_1 = 3/5 xx 1.0 kg = 0.6 kg`. |
|
| 38216. |
The unit of torque and work are same but they are not a same physical quantity? Why? |
| Answer» SOLUTION :TORQUE is a VECTOR while WORK is a SCALAR | |
| 38217. |
A rubber ball dropped from a height of 20 cm (g = 10 m//s^(2)) falls on the roof of an elevator going up at 2 m/s. If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of |
|
Answer» 20m/s |
|
| 38218. |
Is radius of gyration of a body a constant quantity ? |
| Answer» SOLUTION :No, It CHANGES with the CHANGE in the AXIS of ROTATION | |
| 38219. |
A monkey climbs up and another monkey climbs down a rope hanging from a tree with same uniform acceleration separately. If the respective masses of monkeys are in the ratio 2:3, the common acceleration must be |
|
Answer» `(G)/(5)` When MONKEY climbs up with acceleration a, `T-m_1 g = m_1 a ` When another monkey climbs down with same acceleration a, ` m_2 g - Tm_2 a ` Adding (i) and (ii), we get `(m_2-m_1 )g=(m_1 +m_2) a` `or(1- (m_1)/(m_2)) g=[(m_1)/(m_2)+1] a or (1- (2)/(3)) g= [(2)/(3) +1]a` ` or 1/3g= (5)/(3)a ora= (g)/(5)` |
|
| 38220. |
A body starts with a velocity (2hat(i) + 3hat(j) + 11 k)m//s and moves with an acceleration (5hat(i) + 5hat(j) - 5k)m//s^(2). What is its velocity afert 0.2 sec ? |
|
Answer» `7hat(i) + 8hat(j) + 6k` |
|
| 38221. |
A mass 'M' is suspended from a light spring an additional mass 'm' added displaces the spring further by a distance 'x'. Now the combined mass will oscillate the spring with a period |
|
Answer» `T = 2pi sqrt((MG)/(x(M + m))) ` |
|
| 38222. |
What is meant by an equation of state ? |
| Answer» Solution :An equation of staterelates pressure, VOLUME and TEMPERATURE of a SYSTEM. | |
| 38223. |
A car of mass 1000kg moves on a horizontal surface. If the road friction amounts to 10% of weight of the car and air resistance amounts to 2% of the weight, the power required to run the car at a uniform speed of 36KMPH is |
| Answer» ANSWER :C | |
| 38224. |
A projectile is fired at a speed of 100 m/s at an angle of 37^(@) above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1 : 3, the smaller piece coming to rest. Find the distance from the launching point to the point where the heavier piece lands. |
Answer» Solution :Internal forces do not affect the motion of the centre of mass, the centre of mass HITS the ground at a position where the original projectile would have landed. The range of the original projectile is `X_(CM)=(2U^(2)sin theta COS theta)/(g)=(2xx10^(4)xx(3)/(5)xx(4)/(5))/(10)m=960m` The centre of mass will hit the ground at this position. As the SMALLER block comes to rest after breaking, it falls down vertically and hits the ground at HALF of the range, i.e., at x = 480 m. If the heavier block hits the ground at `x_(2)`, then `X_(CM)=(m_(1)x_(1)+m_(2)x_(2))/(m_(1)+m_(2))rArr 960 =((m)(480)+(3m)(x_(2)))/((m+3m))` `therefore x_(2)=1120m` |
|
| 38225. |
Two coherent narrow slits emitting wavelength lambda in the same phase are placed parallel to each other at a small separation of2lambda, the sound is detected by moving a detector on the screen S at a distance D (gtgt lambda) from the slit S_(1) as shown in Fig. 7.76. Find the distance x such that the intensity at P is equal to the intensity at O. |
|
Answer» `Delta = S_(1) P - S_(2) P = S_(1) Q` ` = 2 lambda cos theta` And we have at point `P` , path difference `Delta = lambda` , thus `Delta = 2 lambda cos theta = lambda` `cos theta = (1)/(2)` `theta = (pi)/(3)` Thus the VALUE of `x` can be written as ` x = D tan theta` ` = D tan ((pi)/(3)) = sqrt(3) D` 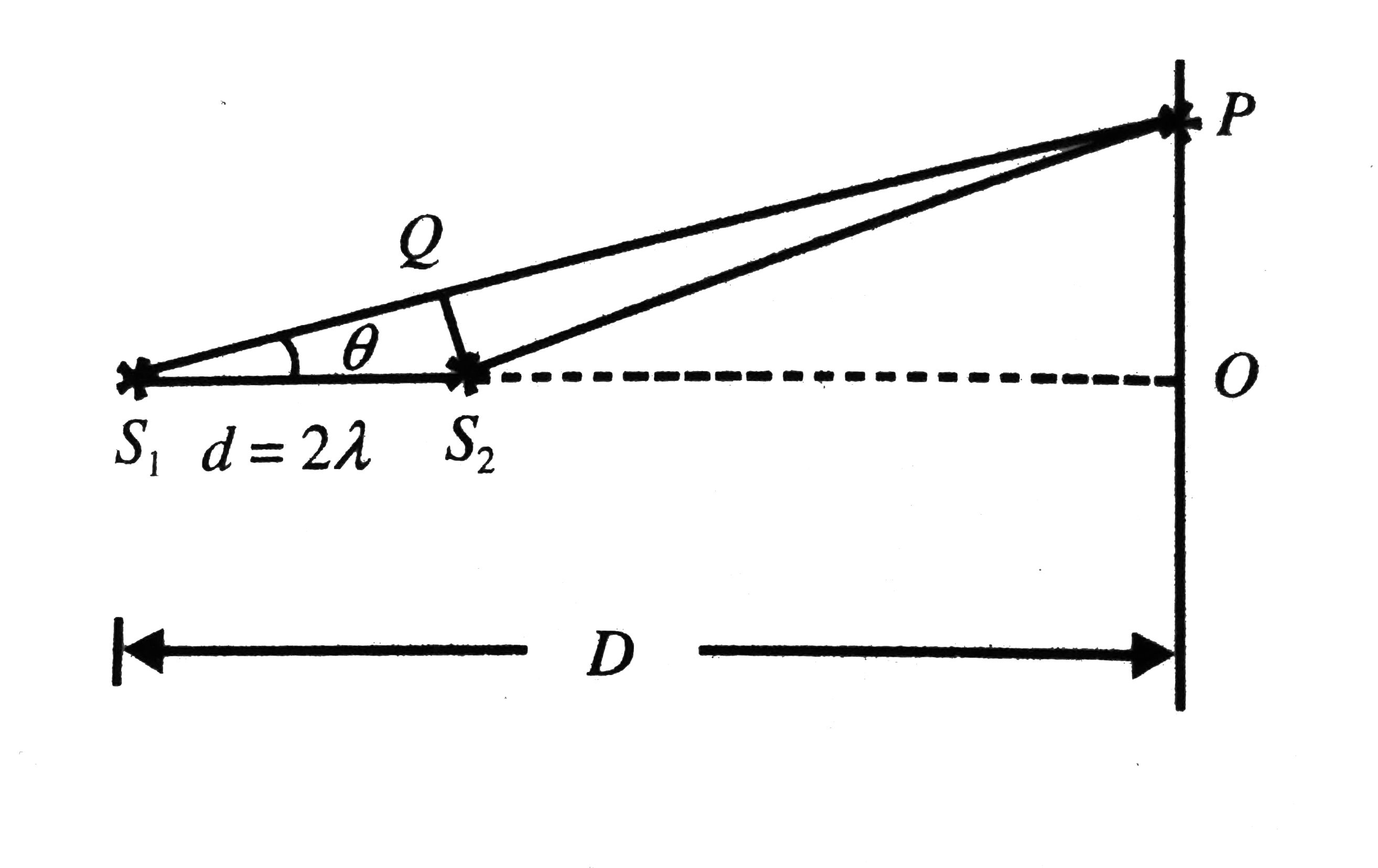
|
|
| 38226. |
The angle of contact between drop of water and material of raincoat is acute angle. |
|
Answer» |
|
| 38227. |
Derive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane. |
|
Answer» Solution :Let us consider a disc of mass M and radius R. It is found that thisdisc is made up of many infinitesimally small rings as shown in the figure. Consider ONE such ring of mass (dm) and thickness (dr) and radius (r). The moment of inerita (dI) of this small ring isgiven by `dI=(dm)r^(2)` As the mass is uniformly distributed the mass per unit AREA `(sigma)` is `sigma=("mass")/("area")=M/(piR^(2))` 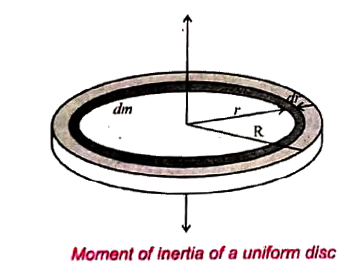 The mass of the infinitesimaly small ring is given by `dm=sigma 2pirdr-M/(piR^(2)) 2PI r dr` where tehh term `(2pir dr)` is the area of this elemental ring where `2pir` is the LENGTH and dr is the thickness. `:.dm=(2M)/(R^(2))rdr` `:.dI=(2M)/(R^(2))r^(3)dr` The moment of inertia (I) of the entire disc is, `I=intdI` `I=int_(0)^(R)(2M)/(R^(2))r^(3)dr=(2M)/(R^(2))int_(0)^(R)r^(3)dr` `K=(2M)/(R^(2))[(r^(4))/4]_(0)^(R)=(2M)/(R^(2))[(R^(4))/4-0]` `I=1/2MR^(2)` |
|
| 38228. |
What is the angle between velocity and acceleration at the highest point of a projectile motion? |
| Answer» SOLUTION :`90^(@)` | |
| 38229. |
State the explain the law of conservation of momentum of the system of particle. |
|
Answer» <P> Solution :Newton.s second law for the system of particle, `(dvecp)/(dt)=vecF_(EXT)`If the sum of external forces acting on the system of particles is zero then `(dvecp)/(dt)=0` `therefore dvecp=0, therefore vec(p_(1))=vecp_(2)` Means the linear momentum remains constant. (`vecp` = constant) Equation `vecp` = constant, it is equivalent to three scalar equation as following : `p_(x)=C_(1),p_(y)=C_(2),p_(3)=C_(3)` where `p_(x),p_(y),andp_(z)` are the components of linear momentum `vecp` for respective axis X, Y and Z-axis and `C_(1),C_(2)andC_(3)` are constant. ..When external total force acting on a system of particles is zero, then its total linear momentum remains constant... This is known as conservation of linear momentum. From `MvecA=vecF`, here `vecF` is total external force. If `vecF=0` then `MvecA=0` `therefore VECA=0` Means, ..when total external force on system is zero, the velocity of centre of mass remains constant... More over `vecA=(dvecv)/(dt)` then If `vecA=0` then `(dvecv)/(dt)=0` `therefore vecv` is constant. Means, total external force on the system is zero, the velocity of centre of mass remains constant. |
|
| 38230. |
At 0^(@)C, three rods of equal length form an equilateral triangle. Among the three rods, one is made of invar (with neligible expansion) and the other two rods are made of some other metal. When the triangle is heated up to 100^(@)C, the angle between the two rods of the same metal changes to (pi/3-theta). Show that the coefficient of linear expansion of the metal is (sqrt(3)theta)/200""^(@)C^(-1). |
|
Answer» Solution :Suppose at `0^(@)C` the lengths of the RODS are l and the coefficient of linear expansion of the metal of AD and BD is `alpha.` The inner rod AB has no expansion. If `l_(1)` is the length of each of the metal rods AD and BD at `100^(@)C, l_(1)=l(1+100alpha).` A perpendicular DO is DRAWN from the vertex D on AB [Fig. 5.7]. From the trianlge ADO, we GET, `"" (l/2)/sin(pi/6-theta/2)=l_(1)/(sin90^(@))` or, `"" l/(2sin(pi/6-theta/2))=(l(1+100alpha))/1` or, `"" sin(pi/6-theta/2)=1/(2(1+100alpha))` or, `"" sin""pi/6cos""theta/2-cos""pi/6sin""theta/2=1/(2(1+100alpha))` or, `"" 1/2-sqrt(3)/2*theta/2=1/(2(1+100alpha))` `""` [Since `theta` is very small, `sin""theta/2 rarr theta/2 " and " cos""theta/2 rarr 1`] or, `"" sqrt(3)/2*theta/2=1/2-1/(2(1+100alpha))=(100alpha)/(2(1+100alpha))` or, `"" (sqrt(3)theta)/2=(100alpha)/(1+100alpha)=100alpha` `""`[As `100alpha` is very small compared to 1, it is negligible] or, `"" alpha=(sqrt(3)theta)/200""^(@)C^(-1).` 
|
|
| 38231. |
A sysem is supplied power of 10 W. Temperature of the system becomes constant at 50^(@)C. With temperature of surrounding at 20^(@)C. When power is switched off system cools from t^(@)C to (t//m)^(@)C in one minute. The heat capacity of the system is 1200 J//^(@)C. find the limiting value of n. |
|
Answer» `n ge 75` Heat lost in 1 minute = `(dQ)/(dt)xx60(J)=Q` `(dQ)/(dt) = 1/3 (t-20)` Fall in temperature=`t//n` `C = (Q)/(Delta theta) = ((1//3)xx(t-20)xx60)/((t//n))` PUTTING values, `1200=20n=(400n)/(t)` Since `t gt 0` so `20n gt 1200` `n ge 60`. |
|
| 38232. |
A source of sound of frequency 1000 Hzmoves to the right with a speed of 50 m/s relative to the ground. To its right is a reflecting surface noving to the leftobserver to the left of the source in figure. Speed of the sound in air is 330 m/s. |
|
Answer» |
|
| 38233. |
3 moles of a monoatomic gas requires 45 cal heat for 5^(@) C rise of temperature at constant volume, then heat required for 5 moles of same gas under constant pressure for 10^(@) C rise of temperature is (R= 2 "cal/mol/"°k) |
|
Answer» 200 cal |
|
| 38234. |
Thetemperatureof perfect blackbody is 1000 Kand its areais 0.1 m^(2) . Ifsigma =5.67 xx 10^(-8) W m^(-2) K^(-4)calculate the heat radiated in 1 minute ? |
|
Answer» Solution :According to Stefan.s law if Eis theenergyradiated in 1 SEC byunit surfacearea then `E = sigma T^(4)` `therefore ` Total energy radiated , `E = A(sigma T^(4))t = 0.1 xx 5.67xx 10^(-8) xx 1000^(4) xx 60 = 34.02 xx 10^(4) J` |
|
| 38235. |
A rope of negligible mass is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder, if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope? Assume that there is no slipping. |
| Answer» SOLUTION :25 `rad//s^(2),10 m//s^(2)` | |
| 38236. |
the maximmum temperature reached during an atomic explosion was of the order of 10^(7) K. Calculate the wavelength of maximum energy b = 0.293 cm K. |
|
Answer» |
|
| 38237. |
A rigid body is made of three identical thin rods, each of length .L.fastended together in the form of the letter .H.. The body is free to rotate about a horizontal axis that runs along the length of one of the legs of .H.. The body is allowed to fall from rest from a position in which the plane of .H. is horizontal. What is the angular speed of the body when the plane of .H. is vertical? |
|
Answer» Solution :The MOMENT of inertia of the SYSTEM about the axis is `I=(4)/(3) ML^(2)`. By conservation of mechanical energy the lose in PE of body is cqual to the gain in rotationalKE. `:.(3)/(2) mgL=(1)/(2) ((4)/(3)mL^(2)), OMEGA^(2)` on solging `omega=(3)/(2) sqrt((g)/(L))` 
|
|
| 38238. |
Which one of the following statements is an incorrect statement ? |
|
Answer» Sound intensity level is givenby `Delta L=10 log_(10) (I_(1))/(I_(0))` decibel. |
|
| 38239. |
Define radius of gyration Mention, the factors on which it depends |
|
Answer» Solution : Radius of GYRATION (K): It is the EFFECTIVE distance of all the particles of a BODY rotating about the given AXIS Radius of gyration `K=sqrt((r_(1)^(2)+r_(2)^(2)+………r_(a)^(2))/(n))` |
|
| 38240. |
How much steam at 100^(@) C is to be passed into water of mass 100g at 20^(@)c to raise its temperature by 5^(@)C?(Latent heat of steam is 540 cal /g and specific heat of water is 1 cal // g^(@)C) |
|
Answer» 0.4g |
|
| 38241. |
A narrow sound pulse (for example, a short pip by a whistle) is sent across a medium (a) Does the pulse have a definite (i) frequency (ii) wavelength (iii) speed of propagation? (b) If the pulse rate is 1 after every 20s. (that is the whistle is blown for a split of second after every 20s), is the frequency of the note produced by the whistle equal to 1/20 or 0.05Hz? |
|
Answer» SOLUTION :(a) The pulse does not have a definite wavelength or frequency, but has a definite SPEED of propagation (in a non-dispersive medium). (B) No |
|
| 38242. |
Sound waves of wavelength lamdatravelling in a medium with a speed of v m/s enter into another medium where its speed is 2v m/s. Wavelength of sound waves in the second medium is |
|
Answer» `lamda` `implies (v_(1))/( v_(2)) = (lamda _(1))/( lamda_(2)) implies (v)/( 2c) = (lamda)/( lamda_(2)) implies lamda_(2) = 2 lamda ` |
|
| 38243. |
A stone thrown into still water, creates a circular wave pattern moving radially outwards. If r is the distance measured from the centre of the pattern, the amplitude of the wave varies as |
|
Answer» `R ^(-(1)/(2))` But `I prop A ^(2) implies A ^(2) prop I implies A prop sqrtI` `THEREFORE A prop (I)/(sqrtr) implies A prop r ^(-1//2)` |
|
| 38244. |
A block moving in air breaks in two parts and the parts separate |
|
Answer» the TOTAL MOMENTUM must be conserved |
|
| 38245. |
A solid sphere and a solid cylinder of same mass are rolled down on two inclined planes of heights h_(1) and h_(2) respectively. If at the bottom of the plane the two objects have same linear velocities, then the ratio of h_(1):h_(2) is |
|
Answer» `2:3` |
|
| 38246. |
A particle of mass m is attached to one end of a massless spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time t = 0 with an initial velocity u_(0). When the speed of the particle is 0.5u_(0), it collides elastically with a rigid wall. After this collision |
|
Answer» the SPEED of the PARTICLE when it returns to its equilibrium POSITION is `u_(0)` |
|
| 38247. |
Four molecules have speed 2 km/s, 3 km/s. 4 km/s, 5 km/s The rms speed of these molecules in km/s is ............. . |
|
Answer» `SQRT(27/2)` |
|
| 38248. |
The dimensional formula of the product of two physical quantities P and Q is ML^2 T^(-2). The dimensional formula of P//Q is ML^0 T^(-2). Then what are the units of physical quantities P and Q. |
|
Answer» FORCE, VELOCITY |
|
| 38249. |
10^(-6)m^(3) volume of water is taken from the surface to the bottom of a lake to a depth of 200 m inside helake. If the bulk modulus of elasticity of water is 220 atm., then what will be the change in its volume? (Density of water =10^(3)kgm^(-3)) |
|
Answer» SOLUTION :`V=10^(-6)m h=200m, K=220atm` `P_(e)=h rho g=200xx10^(3)xx9.8=19.6xx10^(5)NM^(-2)` i.e. `P_(e)=(19.6xx10^(5))/(1.013xx10^(5))=19.348atm` `DeltaP=P_(2)-P_(1)=h rho g =19.348atm` But `K=(- DELTA PV)/(DELTAV)` i.e. `DeltaV=(-(DeltaP)V)/K=(-19.348xx10^(-6))/220=-0.0879xx10^(-6)m^(3)` `Delta V=-8.79xx10^(-8)m^(3)` i.e. Decrease in the volume will be `879xx10^(-8)m^(3)` |
|
| 38250. |
Statement 1 is false, statement 2 is true. Statement-1: The speed of liquid coming out of the orifice is independent of the nature and quality of liquid in the container. |
|
Answer» Statement-I is TRUE, statement-2 true and statements-2 is a correct EXPLANATION for statements-5 |
|