1.

Two coherent narrow slits emitting wavelength lambda in the same phase are placed parallel to each other at a small separation of2lambda, the sound is detected by moving a detector on the screen S at a distance D (gtgt lambda) from the slit S_(1) as shown in Fig. 7.76. Find the distance x such that the intensity at P is equal to the intensity at O.

Answer» <html><body><p><br/></p>Solution :When detector is at `O`, we can see that the path difference in the two <a href="https://interviewquestions.tuteehub.com/tag/waves-13979" style="font-weight:bold;" target="_blank" title="Click to know more about WAVES">WAVES</a> reaching `O is d = 2 lambda` thus at `O` detector <a href="https://interviewquestions.tuteehub.com/tag/receives-1179339" style="font-weight:bold;" target="_blank" title="Click to know more about RECEIVES">RECEIVES</a> a maximum sound . When it reaches `p` and again there is a maximum sound detected at `P` the path difference between two waves must be `Delta = lambda`. Thus from the figure the path difference at `P` can `Delta = lambda`. Thus from the figure the path difference at `P` can be <a href="https://interviewquestions.tuteehub.com/tag/given-473447" style="font-weight:bold;" target="_blank" title="Click to know more about GIVEN">GIVEN</a> as <br/> `Delta = S_(1) P - S_(2) P = S_(1) Q` <br/> ` = 2 lambda cos theta` <br/> And we have at point `P` , path difference `Delta = lambda` , thus <br/> `Delta = 2 lambda cos theta = lambda` <br/> `cos theta = (1)/(2)` <br/> `theta = (pi)/(<a href="https://interviewquestions.tuteehub.com/tag/3-301577" style="font-weight:bold;" target="_blank" title="Click to know more about 3">3</a>)` <br/> Thus the <a href="https://interviewquestions.tuteehub.com/tag/value-1442530" style="font-weight:bold;" target="_blank" title="Click to know more about VALUE">VALUE</a> of `x` can be written as ` x = D tan theta` <br/> ` = D tan ((pi)/(3)) = sqrt(3) D` 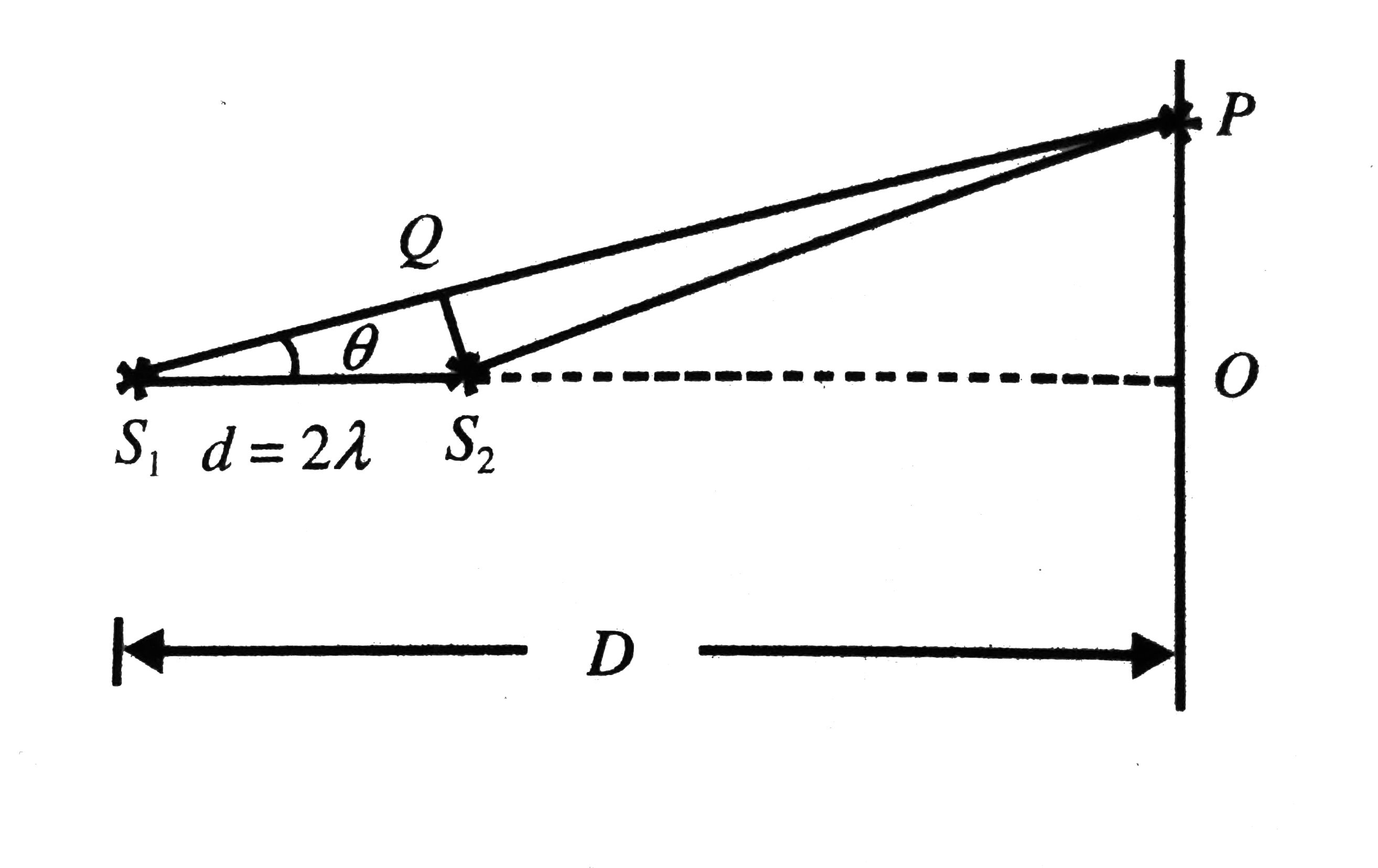<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V06_C07_E01_060_S01.png" width="80%"/></body></html>


Discussion

No Comment Found

Related InterviewSolutions