Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 38751. |
What is the nature of the graph plotted between volume and absolute temperature at constant pressure. Which law it will indicate ? |
| Answer» SOLUTION :It is a STRAIGHT LINE passing through origin, CHARLES Law. | |
| 38752. |
What is the bulk modulus of a perfectly rigid body? |
|
Answer» SOLUTION :INFINITE, because `B = ( P )/(Delta V//V) , Delta V=0` `therefore B =- P /0 = PROP = `infinite |
|
| 38753. |
Two objects of masses 4kg and 3kg are placed along X and T axes respectively at a distance of 1m from the origin. An object of mass 1kg is kept at the origin of the co-ordinatesystem. Calculate the resultant gravitational force attraction on the object at the origin. |
|
Answer» Solution :Force due to 4kg mass on 1kg mass at the origin is `F_(1) = (G xx 4 xx 1)/(1^(2)) = 4G` Force due to 3kg mass on 1 kgmass at the origin is `F_(2) = (G xx 3 xx 1)/(1^(2)) = 3G` The resultant force is found by USING parallelo-gram law of vectors `F = SQRT(F_(1)^(2) + F_(2)^(2) + 2F_(1)F_(2) cos theta)` `= sqrt((4G)^(2) + (3G)^(2) + 2(4g)(3G)cos 90^(@))= 5G` 
|
|
| 38754. |
The radii of two soap bubbles are R_(1)andR_(2). If they coaleasce, then the radius of curvature of the common surface will be |
|
Answer» `R_(2)-R_(1)` |
|
| 38755. |
During forced vibration, the frequency of the external periodic force is |
|
Answer» EQUAL to |
|
| 38756. |
_____are usually made of ____not of copper.[Fill in the blanks] |
|
Answer» |
|
| 38757. |
A definite mass of a gas at 60^(@)C and 80 cm of mercury pressure is compressed slowly. If the final volume is half of the initial volume then the final pressure of the gas is (gamma = 3//2) |
| Answer» Answer :D | |
| 38758. |
If L is the inductance, C is the capacitance and R is the resistance, then R sqrt((C )/(L)) has the dimension |
|
Answer» `MLT^(-2)I^(-2)` |
|
| 38759. |
A metal rope of density 6000kgm^(-3)has breaking stress 9.8xx10^8 Nm^(-2) . This rope is used to measure the depth of the sea. Then the depth of the sea that can be measured without breaking is ---- |
|
Answer» `10 XX 10^3 m` |
|
| 38760. |
At a g_(n) temperature equal masses of monoatomic & diatomic gases are supplied equal quantities of heat. Which of the two gases will suffer a larger temperature rise? |
|
Answer» Solution :(i) The temperature of monoatomic GAS will rise by a large value. (ii) In caes of the monoatomic gas, the heat SUPPLIED is used entirely to increase the TRANSLATIONAL K.E of the MOLECULES. (iii) In case of the diatomic gas. The heat supplies is used to increase the translational, rotational and some times even the vibrational K.E of the molecules. (iv) It is only the translational K.E which INCREASES the temperature. |
|
| 38761. |
Can we use v=romega for a body rolling without sliding? |
| Answer» SOLUTION :No. Because in this SITUATION `vecomega_|_vecr` cannot be MAINTAINED. | |
| 38762. |
A tube is fixed in a vertical plane as shown in figure .Form point A a sphere of mass 0.314 kg is released .During its motionin the tubeitfacesa constant resistiveforce R . At B itsvelocitybecomes zero . Calculate(i) theconstant resistiveforce R and (if) work done byresistive force (average radisu of semicircularpath is 1 m ) . |
|
Answer» Solution :Let D be the lowest point on its path . Let us assume that the potential energy at D to zero , so potential energy at A is , `v_(A) = mgr ""….(1)` `v_(B) = (mgr)/2 ""……(2)` ` [ :. "In right TRIANGLE " Delta OB. B , angle OBB = 30^(@) and OB = r ."Theoppositeside of " 30^(@) " in right triangle is the half value of diagonal "] ` Work DONE by constant resistive force R , `W_(R) = " Force " xx " displacement " ` ` = R xx arc AB ` ` = R xx theta xx r ` ` = R xx (pi/2 +pi/3) r ` ` :. W_(R) = R xx (5pi)/6 r "".....(3)` Now `V_(A)=V_(B) +W_(R)` ` mgr = (mgr)/2 +R (5pi)/6 r ` ` [ :. " From equation (1) ,(2) and (3) "] ` ` :. (mgr)/2= R xx (5pi)/5 r ` ` :.R = (3mg)/(5pi)` ` = (3xx0.314 xx10)/(5xx3.14)` ` :. R = 0.6 N ` Work doneby resistiveforce R, `W_(R) = R xx` displacement ` = R xx arcAB ` ` = R xx(5pir)/6` ` = (0.6 xx 5xx 3.14 xx1)/6` ` :. W_(R) = 1.57 J` |
|
| 38763. |
Determine the amplitude of the resultant displace-ment at x = 0 . |
|
Answer» Solution :Amplitude of resultant DISPLACEMENT at x = 0 , `A = 2 a cos [-((omega_(1) - omega_(2))t)/(2)]= 2 a "cos"((omega_(1) - omega_(2))t)/(2)` |
|
| 38764. |
Show that for a particle executing simple harmonic motion the average value of kinetic energy is equal to the average value of potential energy. |
|
Answer» Solution :Total energy `T.E=(1)/(2)m OMEGA^(2)y^(2)+(1)/(2)m omega^(2)(A^(2)-y^(2))` But`y=a sin omega t` `T.E. =(1)/(2) m omega^(2)A^(2) sin^(2)omega t+(1)/(2)m omega^(2)A^(2) cos ^(2) omega t` `=(1)/(2)m omega^(2)A^(2)(sin^(2) omegatt+ cos^(2) omegat)` From trignometryidentity `Sin^(2)omegat+cos^(2) omega t=1` `:. T.E.=(1)/(2)m omega^(2)A^(2)(1)` `=(1)/(2)m omega^(2)A^(2)` `:. {:("AVERAGE"),("potential energy"):}}= {{:("Average"),("Kinetic energy"):}` `=(1)/(2)` (total energy) |
|
| 38765. |
Among solids,liquids and gases which posseses the greatest Bulk modulus? |
| Answer» SOLUTION :SOLIDS their compressiblity is very SMALL. | |
| 38766. |
The work done per unit volume in stretching a wire is equal to |
|
Answer» STRESS*STRAIN |
|
| 38767. |
Calculate the amount of radiant energy from a black body at a temperature of (i) 27^(@)C(ii) 2727^(@)C.sigma = 5.67xx10^(-8)Wm^(-2)K^(-4). |
|
Answer» |
|
| 38768. |
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. Some which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none at all: (a) y = 2 cos (3 x) sin (10 t) (b) y = 2 sqrt(x - v t) (c ) y = 3 sin (5 x - 0.5 t) + 4 cos(5 x - 0.5 t) (d) y = cos x sin t + cos 2x sin 2t |
|
Answer» SOLUTION :(a) Stationary wave (B) Unacceptable function for any wave (c ) TRAVELLING harmonic wave (d) SUPERPOSITION of TWO stationary waves. |
|
| 38769. |
An L shaped frame is free to rotate in a vertical plane about a horizontal axis passing through a smooth hinge O. Each side of the frame has a length L and mass m. Frame is let to fall with one side horizontal and the other vertical. With what speed the end A will strike the ground ? |
|
Answer» `SQRT(GL)` |
|
| 38770. |
An L shaped frame is free to rotate in a vertical plane about a horizontal axis passing through a smooth hinge O. Each side of the frame has a length L and mass m. Frame is let to fall with one side horizontal and the other vertical. Angular acceleration of the frame just after it is allowed to fall is |
|
Answer» `(4g)/(3L)` |
|
| 38771. |
A uniform dis of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega. A particle of same mass m and having 2 omega R towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Find (A) the angular velocity of the disc. (B) the impulse on the particle due to disc ( C) the impulse on the disc due to hinge. |
Answer» 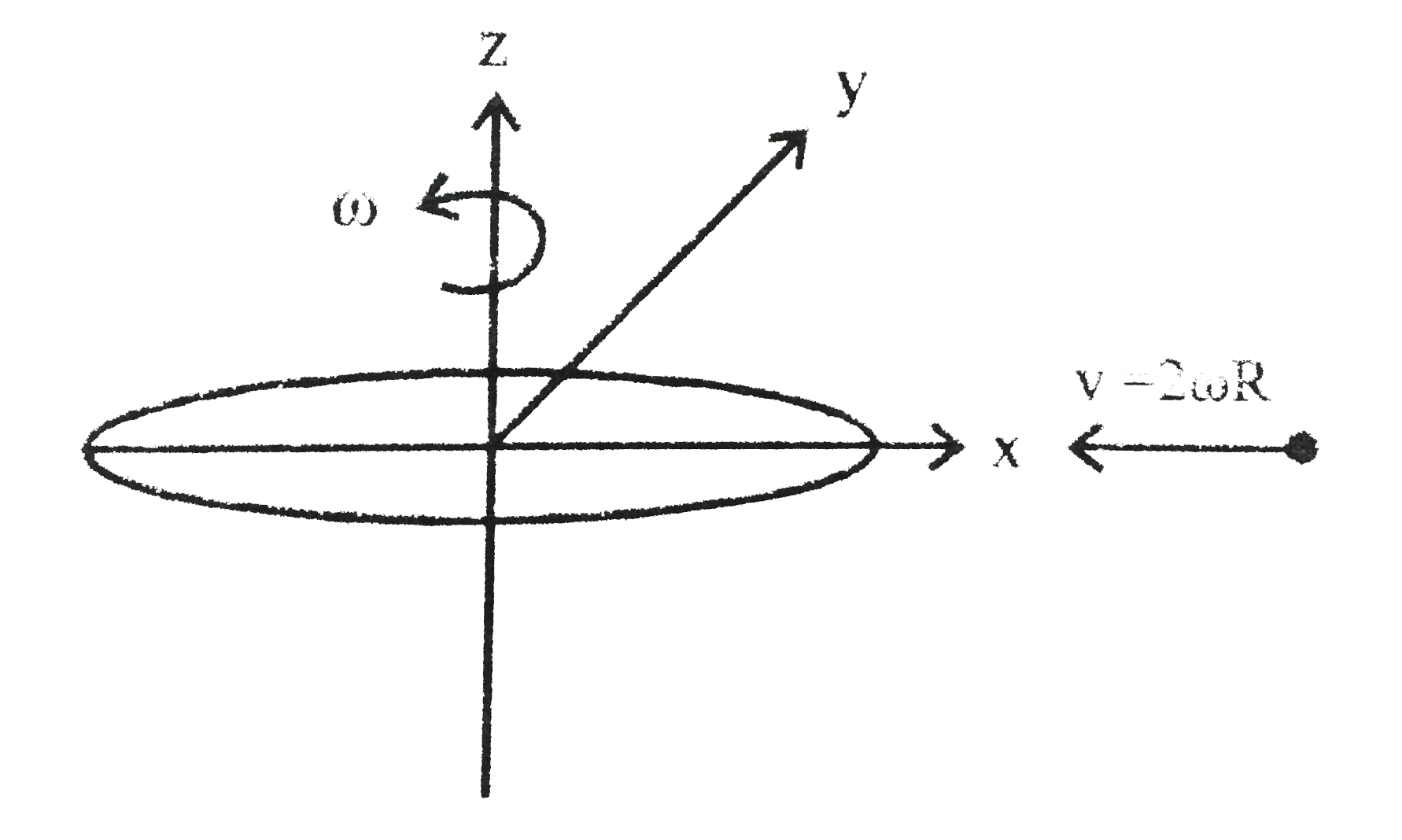 :. `I_(1) omega_(1) = I_(2) omega_(2)` `((1)/(2) mR^(2)) omega =((1)/(2) mR^(2) + mR^(2)) omega_(f)` `(1)/(2) mR^(2) omega = ((3)/(2) mR^(2)) omega_(f)` `omega_(f) = (omega)/(3)` (b) Impulse = change in linear momentum `vec J = mv_(f) hat j - m(2 omega R) (- hat i)` `vec J = m((R omega)/(3)) hat j + 2 m omega R hat i` `|vec J| = sqrt((m(R omega)/(3))^(2) + 2 m omega R^(2))` `|vec J| = mR omega sqrt((1)/(9) + 4) rArr |vec J| = (sqrt(37))/(3) mR omega` ( c) Impulse on disc is EQUAL and opposite to impulse on particle due to disc. :. `J = (sqrt(37))/(3) mR omega`. |
|
| 38772. |
The electron in a hydrogen atom revolves with a velocity 4.13times10^16 rad/sec in an orbit of radius 5.29times10^11m. Calculate its angular momentum (given.m =9.11times10^(-31) kg.) |
| Answer» SOLUTION :1.05 `TIMES 10^(-34)` J.s. | |
| 38773. |
In pure rolling motion of a ring (a) it rotates about instantaneous point of contact of ring and ground (b) its centre of mass moves in translatory motion only (c) its centre of mass will have translatory as well as rotatory motion |
|
Answer» only a is CORRECT |
|
| 38774. |
A horizontal pipe has a circular cross-section but a concial shape. It has a radius of 2 cm at one end and 6 cm at another end. Water enters through wider end with a velocity of 8 cm^(-1). Find the velocity with which it levels the other end. |
| Answer» SOLUTION :72 `CMS^(-1)` | |
| 38775. |
In the cricket game, a batsman strikes the ball such that it moves with the speed 30ms^(-1) at an angle 30^(@) with the horizontal as shown in the figure. The boundary line of the cricket ground is located at a distance of 75 m from the batsman? Will the ball go for a six? (Neglect the air resistance and take acceleration due to gravity g=10ms^(-2). |
|
Answer» Solution :The motion of the cricket ball in air is essentially a projectile motion. As we have already seen, the range (horizontal distance) of the projectile motion is given by `R=(u^(2)SIN2THETA)/(g)` The INITIAL speed `u=30ms^(-1)` The PROJECTION angle `theta=30^(@)` The horizontal distance travelled by the cricket ball `R=((30)^(2)xxsin60^(@))/(10)=(900xx(sqrt3)/(2))/(10)=77.94m` This distance is greater than the distance of the BOUNDARY LINE. Hence the ball will cross this line and go for a six. 
|
|
| 38776. |
A satellite orbits the earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out of the earth’s gravitational influence? Mass of the satellite = 200 kg, mass of the earth = 6.0 ×x 10^(24) kg,radiusof the earth= 6.4 xx 10^(6)m , G = 6.67 xx 10^(-11) N m^(2)) kg^(-2). |
| Answer» SOLUTION :`5.9 XX 10^(9)` J | |
| 38777. |
In an isothermal process, two soap bubble of radius a and b combine and form a bubble of radius c. If the external pressure is p, then prove that the surface tension of the soap solution is T-(p(c^3-a^3-b^3))/(4(a^2+b^2-c^2)). |
|
Answer» Solution :We know , the EXCESS pressure inside the soap BUBBLE = internal pressure - external pressure. `THEREFORE`For the bubble of radius a, excess pressure, `(4T)/(a)=p_a-p` `therefore p_a=(p+(4T)/(a))` Similarly, for the bubble of radius b, `p_b=(p+(4T)/(b))` For the bubble of radius c, `p_c=(p+(4T)/(c ))` Boyle.s law is applicable in isothermal process. According to this law. `p_a V_a+p_b V_b=p_c V_c` or, `(p+(4T)/(a))xx(4)/(3)pia^3+(p+(4T)/(b))xx(4)/(3)pib^3` `=(p+(4T)/(c ))xx(4)/(3)pic^3` or, `(p+(4T)/(a))a^3+(p+(4T)/(b))b^3=(p+(4T)/(c ))c^3` or, `4T(a^2+b^2-c^2)=p(c^3-a^3-b^3)` `therefore T=(p(c^3-a^3-b^3))/(4(a^2+b^2-c^2))`. |
|
| 38778. |
Write SI and CGS unit of heat and give their relation. |
|
Answer» Solution :Its SI unit is JOULE and CGS unit is cal. `:." 1 cal"=4.18` Joule |
|
| 38779. |
A body of mass 5 kg moving on a horizontal surface with a velocity of 10 ms^(-1) comes to rest in 2s. The force required to makes this body move with a velocity of 10 ms^(-1) on the same surface is |
| Answer» Answer :C | |
| 38780. |
A tension of 22N is applied to a copper wire of cross sectional area 0.02"cm"^(2), young's modulus of copper is 1.1 xx 10^(11) N//m^(2) and poisson's ratio 0.32. The decrease in cross sectional area will be |
|
Answer» `1.28 XX 10^(-6) cm^(2)` |
|
| 38781. |
If a sound wave travels from air to water, the quantity that remain unchanged is ………………... |
|
Answer» VELOCITY |
|
| 38782. |
A gas behaves as an ideal gas at : |
|
Answer» LOW PRESSURE and HIGH temperature |
|
| 38783. |
Show that moment of a couple does not depend on the point about which you take the moments. |
Answer» Solution : Consider a couple as shown in Fig. 7.22 ACTING on a rigid body. The forces `F and -F` act respectively at points B and A. These points have position VECTORS `r_(1) and r_(2)` with respect to origin O. Let us take the MOMENTS of the forces about the origin. The moment of the couple = sum of the moments of the two forces making the couple `=r_(1)XX(-F)+r_(2)xxF` `=r_(2)xxF-r_(1)xxF` `=(r_(2)-r_(1))xxF` But `r_(1)+AB=r_(2)`, and hence `AB=r_(2)-r_(1)`. The moment of the couple, therefore, is `AB × F`. Clearly this is independent of the origin, the POINT about which we took the moments of the forces. |
|
| 38784. |
Two cylindrical vessels of equal cross-sectional area. A contain water upto height h_(1) and h_(2). The vessels are interconnected so that the levels in them becomes equal. The work done by the force of gravity during the process is: |
|
Answer» zero |
|
| 38785. |
A lead bullet (specific heat=0.032 cal/gm^(@)C) is completely stopped when it strikes a target with a velocity of 300 m/s. The heat generated is equally shared by the bullet and the target. The rise in temperature of bullet will be |
|
Answer» `16.7^(@)C` |
|
| 38786. |
A uniform disc rotates freely about a fixed perpendicular axis making n_(1) revolutions per minute. Wax of mass m falss vertically and sticks to the disc at distance x from the axis Rotational speed reduced to n_(2) rpm, then moment of inertia of the disc is (n_(2))/(n_(1)-n_(2))"mx"^(n) where 'n' is |
|
Answer» |
|
| 38787. |
Explain hydraulic stress, volume stress and volume strain |
|
Answer» Solution :In above figure, a solid body placed in the fluid under high pressure is compressed uniformly on all sides. The force applied by the fluid acts in perpendicular direction at each point of the surface and the body is said to be under hydraulic compression. As a result this leads to decrease in its volume without any CHANGE of its geometrical shape.The body develops internal restoring FORCES that are equal and OPPOSITE to the forces applied by the fluid. The internal restoring force per unit area in this case is known as hydraulic stress and its MAGNITUDE is equal to the hydraulic pressure (applied force per unit area). The strain produced by a hydraulic pressure is called volume strain and is defined as the ratio of change in volume `(DeltaV)` to the original volume (V) Volume strain `=(Delta )/(V)` It has no units or dimensional formula. |
|
| 38788. |
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R(R = (9)/(7)m). It makes small oscillations about the lowest point. Finds the time period. (Take g = 10m//sec^(2)) |
|
Answer» `5PI SEC` |
|
| 38789. |
A mass is whirled in a circular path with constant angular velocity and its angular momentum is L. If the string is now halved keeping the angular velocity the same, the angular momentum is |
|
Answer» `(L)/(4)` |
|
| 38790. |
What is the temperature at which we get the same reading on both the centigrade and Fahrenheit scales? |
|
Answer» Solution :If X is REQUIRED TEMPERATURE, `X/100=(X-32)/180 impliesX=-40^(0) "(or)"-40^(0)C=-40^@F` |
|
| 38791. |
A body of mass 60 kg is pushed up with just enough force to start in moving on a rough surface with mu_(S)=0.5 and mu_(K)=0.4 and the force continues to act afterwards. What is the acceleration of the body is |
|
Answer» `14.7 MS^(-2)` |
|
| 38792. |
A bullet moving with speed 1.50 m//s strikes a tree and penetrates 3.5 cm beforestopping . Find the magnitude of its acceleration and the time taken to stop . |
|
Answer» |
|
| 38793. |
A wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string. |
|
Answer» Solution :Mass of wheel = m = 1.4 kg Radius = r=0.4 m ANGULAR acceleration of the wheel `=ALPHA`= ? `tau = I alpha = Tr` `1/2 mr alpha = T` tangential acceleration `a = ralpha` `T = 1/2 ma` When the mass falls downwards with an acceleration a, `m_(1)g -T = m_(1)a` `m_(1)g -1/2 ma = m_(1)a` `a(m_(1) + m/2) = m_(1)g, a =(m_(1)g)/(m_(1) + m/2) = (2 xx 9.8)/(2 + (1.4)/2)` Tangential accelerations `=a= 7.26 m//s^(2)` Angular acceleration `=alpha = a/r = (7.26)/0.4 = 18.15 m//s^(2)` Tension in the STRING `=T= 1/2 ma = 1/2 xx 1.4 xx 7.26 = 5.1 N` |
|
| 38794. |
Given a+b+cd+c=0 , which of the following statements are correct? (a) veca, vecb, vecc and vecd must each be a null vector . (b) The magnitude of (veca+vecc) equals the magnitude of (b+d) (c) The magnitude of veca can never be greater than the sum of the magnitudes of vecb, vecc and vecc. (d) vecb+vecc must lie in the plane of vec a and vecd if veca and vecd are not collinear ,and in the line of vec a and vec d, if they are collinear. |
|
Answer» Solution :(a) Incorrect , if is not necessary that `vec a, vecb , vecc` and `vecd` each should be a null VECTOR . `vec a +vec b+vec C +vec d ` can be ZERO by amny other ways . (b)Correct, `vec a+vec b+vec c +vec d =vec0` The `vec a+vecc=-(vecb+vecd)` `|vec a +vec c|=|vecb+vecd|` (c) Correct , `veca +vec b+vec c +vec d =0` `vec a=-(vec b+vec c +vec d)` Magnitude of `veca` can never be grater than `(vec b+vec c+vec d)` (d) `vec a+vec b+vec C+vec d=vec 0` We can write `veca+ (vec b+vec c )+vec d=0` Now `(vec a +vec b+vec c+vec d)` is zero only if`( vec b +vec c )` must LIE in the plane of `veca and vecd` But if `vec a and vec d` are collinear, then `(vec b +vec c)` must lie in theline of `vec a and vec d`, only then the vectorsumofall thevectors will be zero . |
|
| 38795. |
A body of mass sqrt(3) kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30^(@) with the vertical. The value of F and tension in the string are. |
|
Answer» 9.8N, 9.8N |
|
| 38796. |
A simple pendulum of length l has a maximum angular displacement theta. The maximum kinetic energy of the bob of mass m will be |
| Answer» Answer :A | |
| 38797. |
If the earth be at one half of its present distancefrom the sun. How many approximate days will be there in a year ? (Present year of the 365 days. Assume orbit to be circular) |
|
Answer» 365 DAYS `T prop R^(3//2)` `:. T_2/T_1 = ((r_1)/(r_2))^(3//2) = (1/2)^(3/2) =1/((8)^(1/8))` `:. T_(2) = T_(1) xx 1/(2.828)` `:. T_(2) = (365)/(2.828) = 129 . 006` `:. T_(2)-= 129 ` days |
|
| 38798. |
ABCDEF is a regular hexagon with point O as centre. Find the value of vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF). |
|
Answer» SOLUTION :From the diagram `(vec(AB)=-vec(DE))(vec(BC)=-vec(EF))` `vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF)` `=cancelvec(AB)+(cancelvec(AB)+cancelvec(BC))+vec(AD)+(cancelvec(AD)+cancelvec(DE))+(vec(AD)+cancelvec(DE)+cancelvec(EF))` `=3vec(AD)=3(2vec(AO))=6(vec(AO))` |
|
| 38799. |
5.74 g of a substance occupies 1.2cm^(3). Express its density by keeping the significant figures in view. |
|
Answer» SOLUTION :There are 3 SIGNIFICANT figures in the measured MASS whereas there are only 2 significant figures in the measured volume. Hence the density should be expressed to only 2 significant figures. Density =` (5.74)/(1.2) GCM^(-3)` `=4.8 g CM^(-3)`. |
|
| 38800. |
(a) Prove the theorem of perpendicular axes. (b) Prove the theorem of parallel axes. |
|
Answer» Solution :(a) Square of the distance of a point `(X, y)` in the x–y plane from an AXIS through the origin and perpendicular to the plane is `x^(2)+y^(2)` If the centre of MASS of a SYSTEM of n particles is CHOSEN to be the origin `Sigmam_(i)r_(i)=0`. |
|