1.

A uniform dis of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega. A particle of same mass m and having 2 omega R towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Find (A) the angular velocity of the disc. (B) the impulse on the particle due to disc ( C) the impulse on the disc due to hinge.

Answer» 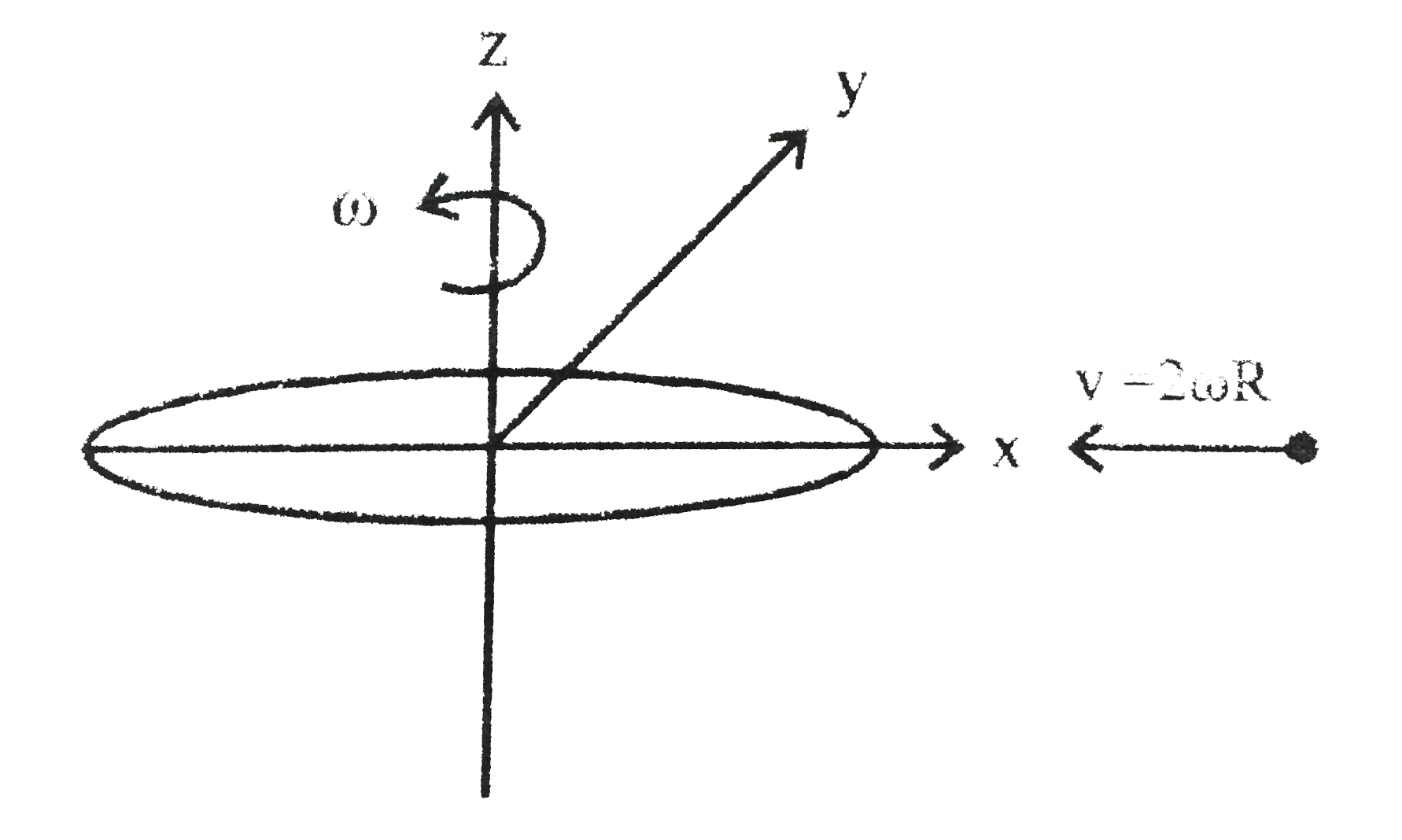<html><body><p><br/></p>Solution :(a) From conservation of <a href="https://interviewquestions.tuteehub.com/tag/angular-11524" style="font-weight:bold;" target="_blank" title="Click to know more about ANGULAR">ANGULAR</a> momentum <br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_MEC_V01_C03_E01_151_S01.png" width="80%"/> <br/> :. `I_(<a href="https://interviewquestions.tuteehub.com/tag/1-256655" style="font-weight:bold;" target="_blank" title="Click to know more about 1">1</a>) omega_(1) = I_(<a href="https://interviewquestions.tuteehub.com/tag/2-283658" style="font-weight:bold;" target="_blank" title="Click to know more about 2">2</a>) omega_(2)` <br/> `((1)/(2) mR^(2)) omega =((1)/(2) mR^(2) + mR^(2)) omega_(f)` <br/> `(1)/(2) mR^(2) omega = ((3)/(2) mR^(2)) omega_(f)` <br/> `omega_(f) = (omega)/(3)` <br/> (b) Impulse = change in linear momentum <br/> `vec <a href="https://interviewquestions.tuteehub.com/tag/j-520843" style="font-weight:bold;" target="_blank" title="Click to know more about J">J</a> = mv_(f) hat j - m(2 omega R) (- hat i)` <br/> `vec J = m((R omega)/(3)) hat j + 2 m omega R hat i` <br/> `|vec J| = sqrt((m(R omega)/(3))^(2) + 2 m omega R^(2))` <br/> `|vec J| = mR omega sqrt((1)/(9) + 4) rArr |vec J| = (sqrt(37))/(3) mR omega` <br/> ( c) Impulse on disc is <a href="https://interviewquestions.tuteehub.com/tag/equal-446400" style="font-weight:bold;" target="_blank" title="Click to know more about EQUAL">EQUAL</a> and opposite to impulse on particle due to disc. <br/> :. `J = (sqrt(37))/(3) mR omega`.</body></html>


Discussion

No Comment Found

Related InterviewSolutions