Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 43301. |
(A): In the following circuit, emf is 2V and internal resistance of the cell is 1Omega and R=1Omega then reading of the voltmeter is 1V. (R ) : V = E-IR where E = 2V, I = 2//2 = 1A |
|
Answer» Both 'A' and 'R' are true and 'R' is the correct EXPLANATION of 'A' |
|
| 43302. |
The speed of electron in the first Bohr orbit is (c/137). The speed of electron in second Bohr orbit is: |
|
Answer» `(2C)/137` |
|
| 43303. |
Compute the typical de-Broglie wavelength of an electron in a metal at 27^(@)C and compare it with the mean separation between two electrons in a metal which is given to be about 2xx10^(-10)m. |
|
Answer» Solution :Electrons in metal behave like ann electon gas. For electron `lamda_("de-Broglie")=(h)/(p)=(h)/(sqrt(3mk_(B)T))=(6.63xx10^(-34))/(sqrt(3xx.911xx10^(-31)xx1.38xx10^(-23)xx300))=6.2xx10^(-9)m` Given `r=2xx10^(-10)m` `THEREFORE (lamda_("de-Broglie"))/(r)=(6.2xx10^(-9))/(2xx10^(-10))=31` Therefore, `lamda_("de-Broglie")gtgt`mean separation between electrons in a metal. |
|
| 43304. |
A 100 watt immersion heater is placed in a pot containing 1 litre of waterr at 20^(@) C. How long will it take to heat water to boiling temperature if 20% of the available energy is lost to surroundings? |
|
Answer» 60 minutes |
|
| 43305. |
In Fig., particles 2 and 4, of charge -e are fixed in place on a y axis, at y_(2) = -10.0 cm and y_(4) = 5.00 cm. Particles 1 and 3, of charge -e can be moved along the x axis. Particle 5, of charge +e, is fixed at the origin. Initially particle 1 is at x_(1) = -10.0 cm and particle 3 is at x_(3) = 10.0 cm (a) To what x value must particle 1 be moved to rotate the direction of the net electric force vec(F)_("net") on particle 5 by 60^(@) counterclockwise? (b) With particle 1 fixed at its new position, to what x value must you move particle 3 to rotate vec(F)_("net") back to its original direction ? |
| Answer» SOLUTION :(a) -402 CM, (B) 4.02 cm | |
| 43306. |
Explain the two modes of long distance communication. |
|
Answer» SOLUTION :The two hasic MODES of long distancecommunication are (1) point-to-point or guided or line communication (2) unguided or space communication, called BROADCAST. Line communication is a transmission system in a FIXED (land-hased) telecommunioation network that uses transmission Lines as a communication channel. Space commumication is a transmission system in a fixed (land-based) as well as mobile (maritime, aeronautical abd land-based) telecommunications network that uses the physical space surrounding us as the communication channel. Space communication is via radio waves in CERTAIN internationally agreed frequency bands. |
|
| 43307. |
Two infinitely long rods carry equal linear denisty lambda each. They are perpendicular to each other and they are in different planes and separated by a distance d. Find the electrostatic force on once rod due to the other |
|
Answer» |
|
| 43308. |
If the minimum possible de-Broglie wavelength of an electron emitted from a photo-cell is 5.477 Å, then the minimum magnitude of potential difference required to stop the photo current in photo cell will be (in volt) : |
|
Answer» 6 `lambda_("min")=sqrt((150)/(V_(s))) rArr V_(s)=(150)/(lambda_("min"^(2)))"volt"(Å)^(2)` `V_(s)=(150)/((1.8257)^(2)="45 volt"` |
|
| 43309. |
Two cells A and B each of 2V are connected in series to an external resistance R = 1 ohm. The internal resistance of A is r_(A)=1.9 ohm and B is r_(B)=00.9 ohm. Find the potential difference between the terminals of A. |
|
Answer» SOLUTION :TOTAL current through the circuit `i=("voltage")/("Total resisance")` `=(4)/((1+1.9+0.9))=(4)/(3.8)A`  potential difference at A, `V_(A)=epsilon-ir =2-(4)/(3.8)xx1.9=2-2=0`. |
|
| 43310. |
The displacement of a particle as a function of time is shown in figure. The figure indicates that (##MOT_CON_NEET_PHY_C23_E02_025_Q01.png" width="80%"> |
|
Answer» the PARTICLE starts with a CERTAIN velocity , but the motion is retarded an finally the particle stops |
|
| 43311. |
A parallel plate capacitor A is filled with a dielectric whose dielectric constant varies with applied voltage as K = V. An identical capacitor B of capacitance C_0 with air as dielectric is connected to voltage source V_0 = 30 V and then connected to the first capacitor after disconnecting the voltage source. The charge and voltage on capacitor. |
|
Answer» ` A are 25 C_0 and 25V ` |
|
| 43312. |
A block of mass 10 kg lying on a smooth horizontal surface is being pulled by means of a rope of mass 2 kg. If a force of 36N is applied at the end of the rope, the tension at the mid point of the rope is, |
|
Answer» 33 N |
|
| 43313. |
The viscosity of mercury decreases with the rise in temperature (Table 21.1a). Check whether relation (34.10) is valid for mercury. Calculate the activation energy. |
Answer» Solution :To check the exponential dependence of viscosity on temperature, find the dependence of the logarithm of viscosity on the reciprocal of the temperature. To do this, compile a NEW table (Table 21.1b) using the data of Table 21.1a. Using the data of the new table, plot  a graph on millimetre graph paper (FIG. 21.1). Almost all the points are SEEN to fall on the straight line `y=a+bx, or log (10^(8) eta)=a+10^(0)+(b)/(T)=a+(B)/(T)`  Taking antilogarrithms we obtain `10^(3)eta=Axx10^(B//T)` the distinction from formula (34.10) being only in numerical coefficients. To find the activation energy e, use two points lying on the straight line: `x_(1)=2.75, y_(1)=0.100 and x_(2)=3.60, y_(2)=0.213` The TEMPERATURES corresponding to these points are `T_(1)=10^(3)//x_(1)=364 K and T_(2)=10^(3)//x_(2)=278K ` and the corresponding visocsities are `eta_(1)=10^(-3)xx10 y_(1)=1.26xx10^(-3)` Pa, * s and `eta_(2)=1.63xx10^(-3)Pa*s`. The ratio or the viscosities is `eta_(2):eta_(1)=e^(epsi_(0)//kT_(e)), epsi^(epsi_(0)//hT_(1))=exp {(epsi_(0)(T_(1)-T_(2)))/(kT_(1)T_(2))}` Hence we obtain after taking the logarithms `(epsi_(0)(T_(1)-T_(2)))/(kT_(1)T_(2))=ln(eta_(2))/(eta_(1))` or `epsi_(0)=(kT_(1)T_(2)ln(eta_(2)//eta_(1)))/(T_(1)-T_(2))-(2.3kT_(1)T_(2)log(eta_(2)//eta_(1)))/(T_(1)-T_(2))` |
|
| 43314. |
A haploid parent produces gametes by......A. ... .division while diploid parent produces gametes by...... B.... Division. |
|
Answer» a-mitotic, b-meiotic |
|
| 43315. |
A string under a tension of 129.6 N produces 10 beats per sec when it is vibrated along with a tuning fork. When the tension in the string is increased to 160 N, it sounds in unison with the same tuning fork, Calculate the fundamental frequency of the tuning fork. |
| Answer» ANSWER :A | |
| 43316. |
A photo- cell employsphotoelectriceffecttoconvert |
|
Answer» Changeinthefrequencyoflightintoachangein electricvoltage |
|
| 43317. |
A particle of mass 6.0 g moves at 4.0 km//s in an xy plane, in a region with a uniform magnetic field given by 5.0//mT. At one instatnt, when the particles velocity is directed 37^(@) counterclockwise from the positive direction of the x-axis, the magnetic force on the particle is 0.45hatk N. What is the particle's charge? |
|
Answer» |
|
| 43318. |
A resistor of 12 Omega, a capacitor of reactance 14 Omega and a pure inductor of inductance 0.1 Hz are joined in series and placed across a 200 V, 50 Hz a.c. supply. Calculate (i) The current in the circuit and (ii) The phase angle between the current and the voltage. Take pi = 3. |
|
Answer» |
|
| 43319. |
Ideal semiconducting materials for solar cell fabrication are those whose band gap is |
|
Answer» close of 1.5 eV |
|
| 43320. |
Give the differential equation for an LC oscillator. |
|
Answer» Solution :`(d^(2)q)/(DT^(2))+((1)/(LC))q=0` (Std - equation of SHM is `(d^(2)x)/(dt^(2))+omega_(0)^(2)x=0`) Note : Comparing the TWO we get `omega_(0)=(1)/(sqrt(LC))` |
|
| 43321. |
A car is moving in a circular horizontal track of radius 10m with a constant speed of 10 ms^(-1) 1. A plumb bob is suspended from the roof of the car by a string of length 1m. The angle made by the string with vertical is (g=10 ms^(-2)) |
|
Answer» `0^(0)` |
|
| 43322. |
The optical vectors of two interfering light waves are E_1 = 2 sin omega tand E_2 = 5 sin (omega t +pi/3). Find the resultant amplitude. |
| Answer» SOLUTION :`sqrt39` CM | |
| 43323. |
When an a.c. source is connected to an ideal capacitor, show that the average power supplied by the source over a complete cycle is zero. |
|
Answer» SOLUTION :Let an ALTERNATING voltage `V = V_(m) sin omega t`is applied across an ideal capacitor, then current setup in the CIRCUIT is given by `I = I_(m) sin (omega t + pi/2)` `therefore` Average power for one complete cycle of circuit will be `P_(av) = 1/T int _(0)^(T) V I dt = 1/T int_(0)^(T) V_(m) sin omega. I_(m) sin(omega t + pi/2). dt = (V_(m)I_(m))/2 int_(0)^(T) sin OMEGAT.cos omegat dt` `=(V_(m)I_(m))/(4 o mega T) [-cos 4PI + cos 0] = (V_(m)I_(m))/(4 omega T) [-1+1]=0` |
|
| 43324. |
In a full wave rectifier circuit operating from 50Hz mains frequency, the fundamental frequency in the ripple would be |
| Answer» ANSWER :C | |
| 43325. |
Flux passes through coil changes from 2xx10^(-3) Wb to 3xx10^(-3)Wb during 25s. The induced e.m.f. is |
| Answer» Answer :D | |
| 43326. |
Give a brief explanation of solid state semiconductor electronics. |
|
Answer» Solution :Some solid state semiconductor and their junctions offer the possibility of controlling the number and the direction of flow of CHARGE carriers through them. Simple excitations like light, heat or small applied voltage can change the number of mobile charges in a semiconductor. The supply and flow of charge carriers in the semiconductordevicesare within the solid itself. The devices of solid state electronics are as follows: (1) Junction diode : It has two electrodes. (2) Transistor : It has three electrodes. (3) Integrated CIRCUIT : It CONTAINS NUMEROUS electrodes. |
|
| 43327. |
How much average power is stored in an inductor when it is connected with AC source? |
|
Answer» `1/2 Li^2` |
|
| 43328. |
What is expression for magnifying power of astronomical telescope? |
|
Answer» Solution :m = `f_0/f_e` Where M = MAGNIFYING POWER `f_0` = FOCAL length of the objective `f_e` = focal length of eye PIECE. |
|
| 43329. |
A uniform chain of length L is lying partly on a table the remaining part hanging down from the edge of the table. If the coefficient of friction between the chain and the table is 0.5, what is the minimum length of the chain that should lie on the table, to prevent the chain from slipping down to the ground ? |
|
Answer» `L//3` `(l)/(L)=(mu)/(mu+1)=(0.5)/(0.5+1)=(1)/(3)` `:.(l)/(L)=(1)/(3)impliesl=(L)/(3)` :. Minimum length of chain that lies on the table is `L-l=L-(L)/(3)=(2L)/(3)` So CORRECT choice is (C). |
|
| 43330. |
""_(1)H^(1)+""_(1)H^(1) rarr""_(1)H^(2)+X+""_(1)e^(0)+ energy. The emitted particle is |
|
Answer» NEUTRON |
|
| 43331. |
The co-ordinates of a moving particle at any time 't' are given by x = alphat^(3) and y = betat^(3). The speed of the particle at time Y is given by : |
|
Answer» `sqrt(alpha^(2) + beta^(2))` `v_(y)=(DY)/(dt)=3betat^(2)` `:.|V|=sqrt(v_(x)^(2) + v_(y)^(2))` `=3t^(2)sqrt(alpha^(2)+beta^(2))` |
|
| 43332. |
A parallel beam of white light falls on a convex lens. Images of blue, yellow and red light are formed on other side of the lens at a distance of 0.20 m, 0.205 m and 0.214 m respectively. The dispersive power of the material of the lens will be |
|
Answer» `619/1000` |
|
| 43333. |
Total power consumed when two resistors of resistance R are connected in series is P. How much power is consumed when they are connected in parallel ? |
|
Answer» `(P)/(4)` CONSUMED power is P. when two RESISTORS are CONNECTED in series. Suppose consumed power is `P_(1)` for each `therefore (1)/(P_(1)) + (1)/(P_(1)) = (1)/(P)` (series connection ) `therefore (2)/(P_(1)) = (1)/(p)` `therefore P_(1) = 2 P ` Now power consumed when they are connected in PARALLEL, `therefore P_(2) = P_(1) + P_(1) ` `therefore P_(2) = 2P_(1) ""( "Putting" , P_(1) = 2P)` `therefore P_(2) = 4P` |
|
| 43334. |
Define the terms (i) mass defect, (ii) binding energy for a nucleus and state the relation between the two. For a given nuclear reaction, the B.E./nucleon of the product nucleus/nuclei is more than that for the original nucleus/nuclei. Is this nuclear reaction exothermic or endothermic in nature? Justify your choice. |
|
Answer» Solution :(i) Mass defect `(Delta m),` of any nucleus `""_(Z)^(A) X` is the difference in the mass of the nucleus ( = M) and the sum of masses of its constituent nucleons ( = M.). `therefore Delta m = M.-M` `= [Zm_(p) + (A - Z) m_(n) ] -M` where `m_(p) and m_(n)` DENOTE the mass of the proton and the neutron respectively. (ii) Binding energy is the energy required to separate a nucleus into its constituent nucleons. The relation between the two is `"B. E." = ("mass defect") xx c^(2)`. (iii) There is a release of energy i.e., the REACTION is exothermic. Reason : Increase in B.F/nucleon implies that more mass has been converted into energy. This WOULD result in release of energy. |
|
| 43335. |
A ray of light is incident normally on one of the face of a prism of angle 30^(@) and refractive index sqrt(2). The angle of deviation will be |
|
Answer» `26^(@)` |
|
| 43336. |
Water is in streamline flow along a horizontal pipe with nonuniform cross-section. At a point in the pipe where the area of cross-section is 10 cm^(2), the velocity of water is 1 ms^(-1) and the pressure is 2000 Pa. The pressure at another point where the cross-sectional area is 5 cm^(2) is : |
|
Answer» 1000Pa `a_(1)v_(1)=a_(2)v_(2)` `10xx10^(-4)xx1=5xx10^(-4)xxv_(2)` `v_(2)=2m//s` For horizontal pipe `(P_(1))/p+1/2v_(1)^(2)=(P_(2))/p+1/2v_(2)^(2)` `(2000)/(10^(3))+1/2.(1)^(2)=(P_(2))/(10^(3))+1/2.(2)^(2)` `2+0.5=(P_(2))/(10^(3))+2` `rArrP_(2)=500` pascals. So CORRECT choice is (b). |
|
| 43337. |
If the wavelength of incident light falling an a photosensitive material decreases, then |
|
Answer» photoelectric current INCREASES |
|
| 43338. |
A resistor of 200 Omega and a capacitor of 15.0 muF are connected in series to a 220 V, 50 Hz ac source. (a) Calculate the current in the circuit, (b) Calculate the voltage (rms) across the resistor and the capacitor. Is the algebraic sum of these voltages more than the source voltage? If yes, resolve the paradox. |
|
Answer» Solution :Given `R=200OMEGA, C=15.0muF=15.0xx10^(-6)F` `V=220V, v=50Hz` (a) In order to calculate the current, we need the impedance of the circuit. It is `Z=sqrt(R^(2)+X_(C)^(2))=sqrt(R^(2)+(2pi vC)^(-2))` `=sqrt((200Omega)^(2)+(2xx3.14xx50xx15.0xx10^(-6)F)^(-2))` `=sqrt((200Omega)^(2)+(212.3Omega)^(2))` `=291.67Omega` Therefore, the current in the circuit is `I=(V)/(Z)=(220V)/(291.5Omega)=0.755A` (b) Since the current is the same throughout the circuit, we have `V_(R )=IR=(0.755A)(200Omega)=151V` `V_(C )=IX_(C )=(0.775A)(212.3Omega)=160.3V` The algebraic sum of the two voltages, `V_(R ) and V_(C )` is 311.3 V which is more than the source voltage of 220 V. How to resolve this paradox? As you have learnt in the text, the two voltages are not in the same phase. Therefore, they cannot be added like ordinary numbers. The two voltages are out of phase by NINETY degrees. Therefore, the total of these voltages must be obtained using the Pythagorean theorem: `V_(R+C)=sqrt(V_(R )^(2) +V_(C )^(2))` `=220V` Thus, if the phase DIFFERENCE between two voltages is properly taken into account, the total voltage across the resistor and the capacitor is equal to the voltage of the source. |
|
| 43339. |
Using Gauss's law in electrostatics,obtainthe expressionfor electricfielddue to auniformlycharged thin sphericalshell at a point . (i) Outside the shell. (b) Inside the shell. |
|
Answer» <P> Solution :Gauss.s theorem : The totaloutwardelectricflux passing througha closedsurface in air is`(1/epsilon_0)` times the totalchargeenclosedby it . .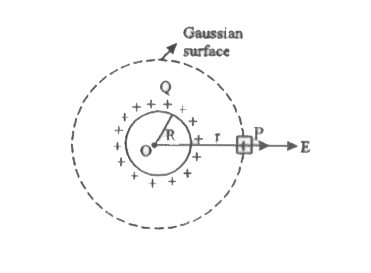 LET .+Q. be the chargeenclosed by a hollowconductorof radius .R.. Let .p. be a POINT at a distance .r. from thecentreof the conductorand .ds. be a smallelement of area surroundingthe point . A normal drawn from the pointcoincides withthe directionof `vecE`. Hence cos `0^@=1`. FromGauss.s theorem , `TOEF=phi=(1/epsilon_0)Q`...(1) by definitionf=E cos q Sds. where,`ads=4pr^2 , cos q=cos 0^@ =1` hence, f=E . `4pr^2`...(2) Comparing(1) & (2) we write`E=(1/(4piepsilon_0))Q/r^2` Fora point on the surface, r =R `E=(1/(4piepsilon_0))(Q/R^2)` This electric fieldintensityis maximum. Sinceelectric fluxdepends on the chargeenclosedand electric fieldintensity depends on the electric flux , electric fieldremainszero at allpoints insidethe sphericalhollow conductor. |
|
| 43340. |
If photons of frequency v are incident on the surfaces of metals. A and B of threshold frequencies (v)/(2)and (v)/(3) respectively, the ratio of the maximum kinetic energy of electrons emitted from A to that from B is |
|
Answer» `2:3` |
|
| 43341. |
In an electromagnetic wave E=100V m^(-1). Find the value of B. |
| Answer» SOLUTION :`B=(E)/C=(100)/(3xx10^8)=3.33xx10^(-7)T` | |
| 43342. |
Find derivative of given functions w.r.t the respective independent variable . y=sin^(3)x+sin3x |
|
Answer» |
|
| 43343. |
A parallel plate capacitor has a plate area 3m^(2), spaced by 3 dielectric slabs of dielectric constant 2,3,6 and of thickness 0.4mm, 0.6 mm and 1.2mm respectively. Find the effective capacity. |
|
Answer» Solution :CAPACITY `C=(epsi_(0)Kd)/(d)=(epsi_(0)A)/(d/K)` Here `C=(epsi_(0)A)/(d_(1)/K_(1)+d_(2)/K_(2)+d_(3)/K_(3))` `d_(1)=0.4 xx 10^(-3) =4 xx 10^(-4)m, K_(1)=2""d_(2)=0.6xx 10^(-3)=6 xx 10^(-4)m, K_(2)=3` `d_(3)=1.2 xx 10^(-3)=12 xx 10^(-4)m, K_(3)=6` `A=3m^(2)` `C=(8.854 xx 10^(-12) xx 3)/((4/2+6/3+12/6)xx 10^(-4))=(8.854 xx 10^(-12)xx3)/(6 xx 10^(-4))=4.427 xx 10^(-8)F` |
|
| 43345. |
(A) : Cyclotron does not accelerate electrons. (R) : Mass of electrons is very small. |
|
Answer» Both 'A' and 'R' are TRUE and 'R' is the CORRECT explanation of 'A'. |
|
| 43346. |
Which of the following has least frequency ?IR radiations, visible radiation, radio waves. |
| Answer» SOLUTION :RADIOWAVES. | |
| 43347. |
The propertyof metals which allows to form a thin wires beyond their elastic limit without rupture is |
|
Answer» DUCTILITY |
|
| 43348. |
A point object O is kept at a distance of 30 cm from a convex lens of power + 4D towards its left. It is observed that when a convex mirror is kept on right side at 50 cm from the lens, the image of object O formed by lens-mirror combination coincides with object itself. Calculate focal length of mirror |
Answer» Solution :Image formed by combination COINCIDES with the object itself. It implies that I is the centre of CURVATURE of convex MIRROR. 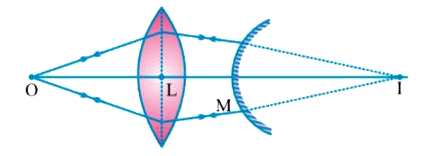 For lens `1/f=1/v-1/u` `1/25=1/v+1/30` `v=150cm` `MI=LI-LM=150-50=100 CM` `f_m=(MI)/2=100/2=50 cm` |
|
| 43349. |
There is change of medium in ? |
| Answer» SOLUTION :REFRACTION | |
| 43350. |
A long charged cylinder of linear charged density lambda is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders? |
| Answer» SOLUTION :`lambda(2 pi epsilon_(0)r)` where r is the DISTANCE of the POINT from the commonaxis of the CYLINDERS. The FIELD is radial, perpendicular to the axis. | |