Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

39851.

A particle in a circular motion covers a distance of 0.5 pi rwhere r is the radius of the circular path. What is the angular displacement ?

Answer»


ANSWER :`90^(@)`
Discussion
39852.

A harmonic osillator is represented by y=0.5cos (1500pi t+0.8) where 'y' and 't' are in 'm' and 's' respectively. Calculate (iv) period

Answer»

SOLUTION :Given, `y=0.5cos(1500pit+0.8)=0.5sin((PI)/(2)-1500pit-0.8)=0.5sin[-1500pit-(0.8-(pi)/(2))]`
`y=-0.5sin[1500pit+(0.8-(pi)/(2))]`
Now (iv) `"period "=(1)/("FREQUENCY")=(1)/(750)=0.00133=1.33xx10^(-3)s.`
Discussion
39853.

A harmonic osillator is represented by y=0.5cos (1500pi t+0.8) where 'y' and 't' are in 'm' and 's' respectively. Calculate (iii) angular frequency

Answer»

SOLUTION :GIVEN, `y=0.5cos(1500pit+0.8)=0.5sin((PI)/(2)-1500pit-0.8)=0.5sin[-1500pit-(0.8-(pi)/(2))]`
`y=-0.5sin[1500pit+(0.8-(pi)/(2))]`
Now (III) angular FREQUENCY `omega=1500pi=4.713xx10^(3)" rads"^(-1)`
Discussion
39854.

300 g of water at 25^(@)C is added to 100 g of ice at 0^(@)C. The final temperature of the mixture is

Answer»

`(-5)/( 3) ° C`
`(-5)/( 2)° C`
`-5^(@) C`
`0^(@) C`

Answer :D
Discussion
39855.

A child stands, hands at the side, on a turntable. The kinetic energy of system is K. The child now raises his arms, and the moment of inertia of system becomes twice. Then the kinetic energy of system will be …………

Answer»

`2K`
`(K)/(2)`
`(K)/(4)`
`4K`

Solution :No EXTERNAL FORCE is acting so angular momentum is constant
`therefore I_(1)omega_(1)=I_(2)omega_(2)`
`therefore omega_(2)=(I_(1)omega_(1))/(I_(2))=(omega_(1))/(2)[because I_(2)=2I_(1)]`
Now rotational kinetic energy
`therefore K_(1)=(1)/(2)I_(1)omega_(1)^(2)` and
`therefore K_(2)=(1)/(2)I_(2)omega_(2)^(2)`
`=(1)/(2)(2I_(1))((omega_(1))/(2))^(2)`
`=(1)/(2)(I_(1)omega_(1)^(2))/(2)`
`=(K)/(2)`
Discussion
39856.

The standard scale of temperature is

Answer»

the MERCURY scale
the gas scale
the platinum RESISTANCE scale
LIQUID scale

Solution :N//A
Discussion
39857.

A lead ball dropped into a take from a diving board 5m above the water hitsthe water with certain velocity and then sinks to the bottom with the same constant velocity. If it reaches the bottom in 3s after it is dropped the depth of the take is (g=10ms^(-2))

Answer»

30m
15m
10m
20m

Answer :D
Discussion
39858.

A particle of mass m _(1) makes a head on elastic collision with a stationary particle of mass m _(2). What fraction of kinetic energy is (a) retained by m _(1) (b) transferred onto m _(2) ?

Answer»

Solution :(a) ` v _(1) = (( m _(1) - m _(2)) u + 2M _(2) (o))/( m _(1) + m _(2)) IMPLIES (( v _(1))/(u ))^(2) = ((m_(1) - m _(2))/(m _(1) + m _(2))) ^(2)`
`implies ((1)/(2) m _(1) v _(1) ^(2))/( (1)/(2) m _(1) u ^(2)) = ((m _(1) - m _(2)) /( m _(1) +m _(2))) ^(2) (KE of 1 ^(st ) " particle finally")/(KE of 1 ^(st) "particle initially") = (( m _(1) - m _(2))/( m _(1) + m _(2))) ^(2)`
`therefore` fraction of KE retained by `1 ^(st)` body `f _(1) = ((m _(1) - m _(2))/( m _(1) + m _(2)) ) ^(2)`
(B) `v _(2) = (2 m _(1) u + ( m _(2) - m _(1)) 0o)/(m _(1) + m_(2)) implies(v _(2))/( u ) = (2m _(1))/( m _(1) + m _(2))`
`f _(2) = ((1)/(2) m _(2) v _(2) ^(2))/( (1)/(2) m _(1) u ^(2))= (m_(2))/( m _(1)) [ ( 2m _(1))/( m _(1) + m _(2)) ] ^(2)`
`therefore f _(2) = ( 4m _(1) m _(2))/( ( m _(1) + m _(2)) ^(2))` (fraction of KE given to `2 ^(nd)` body)
Discussion
39859.

Two capillary tubes of same length but different radii r_1 and r_2 are fitted in parallel to the bottom of a vessel. The pressure head is P. What should be the radius of a single tube that can replace the two tubes so that the rate of flow is same as before

Answer»

`r_(1)^(4) + r_(2)^(4)`
`(r_(1)^(2) + r_(2)^(2) )^(1/4)`
`(r_(1)^(4) + r_(2)^(4) )^(1/4)`
`r_(1) + r_(2)`

ANSWER :C
Discussion
39860.

The specific heat capacity of a gas at constant pressure is greater than that at constant volume because

Answer»

at CONSTANT volume, all the heat supplied GOES to INCREASE the INTERNAL energy of the gas
at constant there is no change in temperature of the gas when heat is supplied
at constant pressure, there is no change in internal energy of the gas when heat is supplied
the gas expands when its temperature increase at constant pressure

Answer :A
Discussion
39861.

A uniform chain of length .L. and mass .m. is on a smooth horizontal table, with (1)/(n) th part of its length hanging from the edge of the table. Find the kinetic energy of the chain as it completely slips off the table.

Answer»

Solution :With respect to the top of the table, the initial potential energy of the chain,
`U_(1)= PE` of the chain lying on the table + PE of the HANGING PART of the chain
`=L(1-(1)/(N))mg(0)+(m)/(n)g(-(L)/(2n))=-(mgL)/(2n^(2))`
P.E of the chain, when it just slips off the table,
`U_(2)=mg((-L)/(2))=-(mgL)/(2)`
From law os conservation of energy
`DELTA K =- Delta U "" K_(f)-K_(i)=-(U_(f)-U_(i))`
`because K_(i)=0 , K_(f)=-[-(mgL)/(2)-(-(mgL)/(2n^(2)))]`
`K_(f)=(mgL)/(2)[1-(1)/(n^(2))]`
If .V. is the velocity of the chain, then,
`(1)/(2)mv^(2)=(mgL)/(2)[1-(1)/(n^(2))] THEREFORE v=sqrt(gL[1-(1)/(n^(2))]`
Discussion
39862.

If the net torque acting on the body is zero, then the body is in

Answer»

TRANSLATIONAL EQUILIBRIUM
ROTATIONAL equilibrium
mechanical equilibrium
none

ANSWER :B
Discussion
39863.

Explain linear expansion .

Answer»

Solution :Increase in length of substance `(Deltal)` is directly proportional to original length ..l.. and increase in TEMPERATURE `..DeltaT..`,
`:.Deltalalphal" and "Deltal alphaDeltaT`
`:.DeltalalphalDeltaT` (combinely)
`:.(Deltal)/(l)alphaDeltaT`
Hence, the fractional change in length. `((Deltal)/(l))` is directly proportional to `DeltaT`.
`:.(Deltal)/(l)propDeltaT`
`:.(Deltal)/(l)=alpha_(l)DeltaT`
`:.Deltal=alpha_(l)lDeltaT` . . . . (1)
Where `alpha_(l)` is coefficient of linear expansion and is characteristic of material.
Value of `alpha_(l)` depends on type of material and temperature.
If the temperature difference is not LARGE then `.alpha_(l).` doesn.t depend on temperature.
Unit of `alpha_(l)` is `(""^(@)C)^(-1)` or `K^(-1)`.
In equation (1), `Deltal=l_(2)-l_(1)` and `DeltaT=T_(2)-T_(1)`,
`l_(2)=l_(1)=alpha_(l)l_(1)(T_(2)-T_(1))`
`:.l_(2)=l_(1)+alpha_(l)l_(1)(T_(2)-T_(1))`
`:.l_(2)=l_(1)[1+alpha_(l)(T_(2)-T_(1))]`
By taking `alpha_(l)=alpha` and `l_(1)=l`
`l_(2)=l[1+alpha(T_(2)-T_(1))]`

In above table, special average values are given for some ELEMENTS for `0^(@)C` to `100^(@)C` temperature interval.
From this table, if `alpha_(l)` for glass and COPPER are compared, then it is seen that for the same increases in temperature, copper expands 5 times more than glass.
In general, expansion is more in METALS and their values of `alpha_(l)` are high.
Discussion
39864.

A monkey of mass 40 kg climbs on a rope (fig) which can stand a maximum tension of 600 N. In which of the following case will the rope break the monkey (a) climbs up with an acceleration of 6 m s^(-2)(b) climbs down with an acceleration of 4 m s^(-2)(c ) climbs up with a uniform speed of 5 m s^(-1) (d) falls down the rope nearly freely under gravity(Ignore the mass of the rope)

Answer»

Solution :(a) When the monkey climbs up with an acceleration of `6 ms^(-2)`, the tension in the ROPE is
`T=m(g+a)=40(9.8+60=632 N`
It is greater than breaking strength (600 N).
So the rope breaks.
(b) When the monkey climbs up withan acceleration of `4 ms^(-2)`, the tension in the rope is
`T=m(g+a)=40(9.8+4)=552N`
It is smaller than breaking strength (600 N). So the rope does not break.
(c ) When the monkey climbs up with an uniform speed of `5 ms^(-1)`, the tension in the rope is
`T=m(g)=40(9.8)=392 N`
It is smaller than breaking strength (600 N). So the rope does not break.
(d) When the monkey falls down the rope nearly freely under gravity then the tension is almost zero. So the rope does not break.
Discussion
39865.

A harmonic osillator is represented by y=0.5cos (1500pi t+0.8) where 'y' and 't' are in 'm' and 's' respectively. Calculate (ii) frequency

Answer»

Solution :GIVEN, `y=0.5cos(1500pit+0.8)=0.5sin((pi)/(2)-1500pit-0.8)=0.5sin[-1500pit-(0.8-(pi)/(2))]`
`y=-0.5sin[1500pit+(0.8-(pi)/(2))]`
Now (ii) frequency `=(OMEGA)/(2K)=(1500pi)/(2PI)=750Hz.`
Discussion
39866.

A cylindrical piece of cork of density of base area A and height h floats in a liquid of density p_(l). The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hp)/(p_(1)g)) where p is the density of cork. (Ignore damping due to viscosity of the liquid).

Answer»

Solution :In equilibrium, weight of the cork equals the up THRUST. When the cork is depressed by an amount x, the net upward FORCE is `Axp_(1)g`. Thus the force constant `k = Ap_(1)g `. Using m = AHP, and `T=2pisqrt(m/k)` one gets the given expression.
Discussion
39867.

The magnitude of potential energy per unit mass of the object at the surface of earth is 'E'. The scape velocity of the object is

Answer»

`SQRT(2E)`
`4E^(2)`
`sqrt(E)`
`sqrt(E//2)`

ANSWER :A
Discussion
39868.

Show that Laplace correction for elasticity of gaseous medium is E = gamma p, where 'gamma' is the ratio of specific heates.

Answer»

Solution :Consider adiabatic variation in the PRESSURE and volume of gasesousmedium.
`PV^(gamma) =0 `
i.e., `gamma PV^(gamma-1) Dleta V + V^(gamma) Delta P = 0`
i.e., Bulk modulus-`( Delta P )/((DeltaV)/( V)) = gamma P`
Hence in the expression`v = sqrt((E )/(rho ))`, Elasticity 'E' is replaced by `gamma P`.
LAPLACE equation is written as `v =sqrt((gamma P )/( rho ))`
Where `gamma = 1+ 2 //f` and'f' is number of degrees of freedom of gaseous molecule.
Discussion
39869.

The temperature of equal masses of three different liquids A, B and C are 12^@C, 19^@C, and 28^@Crespectively. The temperature when A and B are mixed is 16^@Cand when B and C are mixed it is 23^@CWhat should be the temperature when A and C are mixed?

Answer»

`20.26^@C`
`15.87^@C`
`25^@C`
`30^@C`

ANSWER :A
Discussion
39870.

If for hydrogen C_p - C_v = m and for nitrogen C_p - C_v = n, Where C_p and C_vrefer to specific heatsper unit mass respectively at constant pressure and constant volume, the relation between m and n is (molecular weight of hydrogen = 2 and molecular weight or nitrogen = 14)

Answer»

N = 14M
n =7M
m = 7N
m = 14n

Answer :C
Discussion
39871.

How does the gravity change inside the mines ?

Answer»

SOLUTION :DECREASES
Discussion
39872.

A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to

Answer»

`t^(1/2)`
`t`
`t^(3/2)`
`t^2`

ANSWER :B
Discussion
39873.

Which graph corresponds to an object moving with a constant negative acceleration and a positive velocity?

Answer»




ANSWER :B
Discussion
39874.

The magnitude and direction of the accelerationof a body are constant. Will the path of the body necessarily be a straight line ?

Answer»

Solution :If the magnitude as wall as DIRECTION of the acceleration of a body is constant, then it is not necessary the the path of the body is a straight line.
Eg: In projectile motion, the projectile is under acceleration DUE to gravity which has constant magnitude `(9.8 m//s^(2))`and constant direction (vertically DOWNWARD) . The path of projectile is PARABOLIC and not a straight line.
Discussion
39875.

Define rotational motion. Give example.

Answer»

Solution :Ifevery point in the object transverses a circular path about an axis, during a MOTION then the motion is called ROTATION (except the points located on the axis) Eg: Rotation of a disc about an axis through its CENTRE.
Discussion
39876.

One end of V-tube containing mercury is connected to a suction pump and the other end to atmosphere. The two arms of the tube are inclined to horizental at an angle of 45^(@) each. A small pressure difference is created between two columns when the suction pump is removed. Will the column of mercury in V-tube execute simple harmonic motion? Neglect capillary and viscous forces. Find the time period of oscillation.

Answer»

Solution :Figure shown as below

Let SMALL liquid column of length dx is in the left of tube at x height from horizontal
Potential energy due to dx element,
`d(PE)= dmgx""[PE=" from mgh "]`
`=p V gx ""[therefore m= pV" and "V= A dx]`
`=p A dx gx`
`= pA g x dx`
TOTAL potential energy of liquid in left column
`P.E= int_(0)^(h_1) Ap gx"" dx`
`=A pg int_(0)^(h_1) x dx`
`=A pg[(x^2)/(2)]_(0)^(h_1)= (A pg h_(1)^(2))/(2)`
From figure `h_(1)= l sin 45^(@)= (l)/(SQRT(2))`
`therefore P.E = (A p gl^(2))/(4)`
Total potential energy of liquid in V-tube
`P.E= (A pg l^(2))/(4)+ (Apg l^(2))/(4)`
Initial `P.E. = (A pg l^(2))/(4)"""......."(1)`
When the SUCTION pump is removed and due to pressure difference, let element moves towards right side by y unit.
Then the liquid column in left arm `=(l-y)`
And the liquid in right arm `=l+y`
Total potential energy `=Ap g(l-y)^(2) sin^(2) 45^(@)+ Ap g (l+y)^(2) sin^(2)45^(@)`
Final `P.E. = (A pg (l-y)^(2))/(2)+ (Ap g(l+y)^(2))/(2)"""......"(2)`
Potential energy difference
`triangle PE =` final P.E. - initial P.E.
`=(A pg)/(2)[(l-y)^(2)+(l+y)^(2)-l^(2)]""` [From equation (1) and (2) ]
`=(Apg )/(2) [2l^(2)+2y^(2)-l^(2)]`
`=(A pg )/(2) [l^(2)+2y^(2)]"""........"(3)`
If change in velocity v of total liquid column
`triangle KE= (1)/(2)mv^(2)""[" where "m= pV= pA xx 2l]`
`triangle KE = Ap lv^(2)"""......."(4)`
From law of conservation of energy,
`triangle PE + triangle KE= 0`
`A pg (l^(2)+2y^(2))+ APL v^(2) = 0"""........."(5)`
Difference w.r.t time .t.
`Apg [(d)/(dt)(l^(2)+2y^(2))]+ Apl (d)/(dt)(v^2)=0`
`Apg (0+2y(dy)/(dt))+Apl (2v(dv)/(dt))=0`
`2A pg y v + Apl (2v)a=0`
Dividing by `2Apv`,
`gy+la=0""[therefore 2Apv ne 0]`
`therefore a= -(g)/(l)y`, comparing with this to
`(d^(2)y)/(dt^(2))= -omega^(2)y`
`therefore omega = sqrt((g)/(l))`
`therefore (2pi)/(T)= sqrt((g)/(l))`
`therefore T= 2pi sqrt((l)/(g))` is time period.
Discussion
39877.

A spring balance has a scale which ranges from 0 to 25 kg and the length of the scale is 0.25 m. It is taken to an unknown planet X where the acceleration due to gravity is 11.5ms^(-1). Suppose a body a mass M kg is suspended in this spring and made to oscillate with a period of 0.50 s. Compute the gravitational force acting on the body.

Answer»

Solution :Let us first calculate the stiffness constant of the spring balance by USING equation `(m)/(k)=(l)/(g)`
`k=(mg)/(l)=(25xx11.5)/(0.25)=1150Nm^(-1)`
The time period of oscillations is given by `T=2pisqrt((M)/(k))`, where M is the mass of the BODY.
Since, M is unknown, rearranging, we get
`M=(KT^(2))/(4pi^(2))=((1150)(0.5)^(2))/(4pi^(2))=7.3kg` `M=(kT^(2))/(4pi^(2))=((1150)(0.5)^(2))/(4pi^(2))=7.3kg`
The GRAVITATIONAL force ACTING on the body is
`W=Mg=7.3xx11.5=83.95N~~84N`
Discussion
39878.

One mole of an ideal gas undergoes a process such thatP prop 1/sqrtT . The molar heat capacity of thisprocess is 4R, where R is universal gas constant. Then,

Answer»

the work DONE by the gas is 1.5 `RDelta T`where `DeltaT`is the CHANGE in temperature
DEGREE of freedom of the gas is 5
on INCREASE of temperature, volume increases
on increases of temperature, volume decreases

Answer :A::B::C
Discussion
39879.

A wedge of mass M rests with one face in contact with horizontal , smooth surface . A particle of mass m is placed on the smooth face on it , inclined at an angle alphato the horizontal and released . Find the velocity of the wedge and that of the particle relative to the wedge when the particle has slipped a distance x down the face of the wedge . Also calculate the acceleration of the wedge and that of the particle relative to the wedge and the smooth surface . [Hint : Apply principal of conservation of momentum along the horizontal and energy conservation principle . See Example 8 )

Answer»


Answer :`sqrt((2 m^(2)G x "SIN"alpha COS^(2) alpha)/((M + m) (M + m sin^(2)alpha))) ,sqrt((2(M+ m) g x "sin"alpha)/(M + m sin^(2) alpha)) ((M + m) g "sin"alpha)/(M + m sin^(2)alpha) , (mg"sin" alpha "cos"alpha)/(M + m sin^(2) alpha)`
Discussion
39880.

A partilcle moves according to the law x = a cos""(pi t)/(2). The distance covered by it in the time interval between t = 0 to t =3 sec is

Answer»

2a
3a
4a
a

Answer :B
Discussion
39881.

A 2 kg ball moving at 24 ms undergoes inelastic head on collision with a 4 kg ball moving in the opposite direction at 48 ms. If the coefficient of restitution is 2/3, their velocities in ms-after impact are

Answer»

`-56, -8`
`-28, -4`
`-14, -2`
`-7,-1`

Answer :A
Discussion
39882.

The temperature of 20 g of oxygen gas is raised from 50^(@)C to 100^(@)C. (i) At constant volume. Find out the amount of heat supplied and the rise in internalenergy in case. Given , R = 2 cal cdot mol^(-1) cdot K^(-1) , for oxygen, c_(v) = 0.155 cal cdot g^(-1) cdot^(@)C^(-1).

Answer»

Solution :HEAT supplied at constant VOLUME,
`Q_(v) = mc_(v) (t_(f) - t_(i))`
`=20 xx 0.155 xx (100-50) = 155 cal`
Work done, W = 0
So, rise in internal ENERGY ,
`U_(f) - U_(i) = Q - W = 155 - 0 = 155 cal`
`= 155 xx 4.2 J = 651 J`.
Discussion
39883.

The time period of a mass loaded spring is .T.. If 20% of its turns are cut and removed, the same massis attached to the remaining spring would oscillate with a time period of

Answer»

`(5T)/(4)`
`(SQRT(5)T)/(2)`
`(4T)/(5)`
`(2T)/(sqrt(5))`

ANSWER :D
Discussion
39884.

A truck starts from rest and accelerates uniformly at 2.0 m s^(-2).At t = 10 s, a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What are the (a) velocity, and (b) acceleration of the stone at t = 11s ?(Neglect air resistance.)

Answer»

SOLUTION :(a)Velocity of car ( at t = 10 s ) =` 0 + 2 x× 10 = 20 m s^(-1)`
By the First Law, the HORIZONTAL component of velocity is` 20 m s^(-1)`throughout. Vertical component of velocity (at t = 11s) ` = 0 + 10 xx 1 = 10 ms^(-1)`
Velocity of stone (at t = 11s) ` = sqrt( 20^2 + 10^2) = sqrt 500 = 22.4 ms^(-1)` at an angle of `tan^(-1) (1//2)` with the horizontal. (b) `10 ms^(-2)` vertically DOWNWARDS .
Discussion
39885.

If R is the Rydberg constant, C is the velocity and h is the Planck's constant, then RCh has the dimensions of

Answer»

power
Angular frequency
Wavelength
Energy

Answer :D
Discussion
39886.

For a prism of refractive index 1.732 the angle of minimum deviation is equal to the angle of the prism. The angle of prism is

Answer»

`30^@`
`45^@`
`60^@`
`80^@`

ANSWER :C
Discussion
39887.

Suppose universal gravitational constant starts to decrease, then (a)length of the year will decrease (b) earth will folllow a spiral path of decreasing order (c) kinetic energy of earth will decrease

Answer»

only a and B are TRUE
only a and C are true
only b and c are true
all are true

ANSWER :B
Discussion
39888.

A clock regulated by a seconds pendulum keeps correct time. During summer the length of the pendulum increases to 1.01 m. How much will the clock gain or loose in one day ?

Answer»

SOLUTION :752.9 s LOSES TIME
Discussion
39889.

In CGS system the magnitude of the force is 100 dyne.In another system where the fundamental physical quantities are kilogram, metre and minutc, the magnitude of the force is

Answer»

`0.036`
`0.36`
`3.6`
`36`

ANSWER :C
Discussion
39890.

Three identical masses are kept at the corners of an equilateral triangle ABC. A moves towards B with a velocity V,B moves towards C with velocity V and C moves towards A with same velocity V. Then the velocity of centre of mass of the system of particles is

Answer»

V
zero
3V
`(V)/(3)`

ANSWER :B
Discussion
39891.

Starting from rest a wooden block moves with a velocity of 25 ms^(-1) along a rough ground and comes to rest. Calculate the distance travelled by the wooden block on the rough surface of coefficient of friction 0.25.

Answer»

50M
75m
100m
125m

Answer :D
Discussion
39892.

Calculate the power of an engine which can pull a mass of 500 metric ton up an incline rising 1 in 100 with a velocity of 10 m/s.

Answer»

Solution :`sin theta = (1)/(100)`, Velocity = 10 m/s , Mass m = 500 metric ton `= 500 XX 10^(3)` kg
F = Force applied , `= 500 xx 10^(3) xx 9.8 xx (1)/(100) = 49 xx 10^(3)` N
Power `P = F upsilon = 49 xx 10^(3) xx 10 = 49 xx 10^(4)` watts = 490 kw.
Discussion
39893.

A body subjected to strain a number of times does not obey Hooke.s law due to

Answer»

YIELD point
Breaking stress
Elastic fatigue
Permanent set

Answer :3
Discussion
39894.

Two particles having mass M and m are moving in a circular path having radius R and r. If their time period are same then the ratio of angular velocity will be

Answer»

`(R)/(R)`
`(R)/(r)`
1
`SQRT((R)/(r))`

ANSWER :C
Discussion
39895.

A uniform slender rod of length L, cross -sectional area A and young's modulus Y is acted upon the forces shown in figure. The elongation of the rod is

Answer»

`(3FL)/(5AY)`
`(2FL)/(5AY)`
`(3FL)/(8AY)`
`(8FL)/(3AY)`

ANSWER :D
Discussion
39896.

Draw graphs a to t, v to t and x to tfor the object falling freely.

Answer»

SOLUTION :
For object FALLING freely, ACCELERATION is constant and equation to negative g. Thus, graph (a) shows the change in acceleration with respect to time `(a to t ).`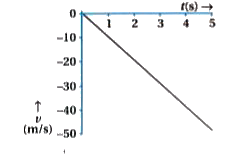

VELCITY of object falling freely, `v =- g t.` THus, graph (b) is obtained for `v to t.`

For object falling freely, `h = 1/2 g t ^(2).` Thus graph (c) is obtained for `x to t.`
Discussion
39897.

In increasing the area of a film of soap solution from 50 "cm"^(2)" ""to"" "100"cm"^(2) 3xx10^(-4) J of work is done. Calculate the value of surface tension of the soap solution.

Answer»


ANSWER :`(3XX10^(-2)NM^(-1))`
Discussion
39898.

A thin liquid convex lens is formed in glass, Refractive index of liquid is 4//3. And that of glass is 3//2. If f. is the focal length of the liquid lens in air, its focal length and nature in the glass is

Answer»

`f_1` CONVEX
`F,` concave
2f,concave
3f,concave

Answer :D
Discussion
39899.

A man is sitting in a boat which is floating in a pond. If the man drinks some water from the pond, what will happen to the level of water in the pond?

Answer»

Solution :If the mandrinks m gram of water from thepond, te WEIGHT of (boat + MAN) system will increase by mg and so the system will displace m gram more water for floating. So due ot removal FO water from pond, the water level in pond will fall but due to water displaced by the floating system the water level in the pond will rise and so the water REMOVED FORM the pond is equal to the water displaced by the system, the level of water in the pond will remain unchanged.
Discussion
39900.

A running man has the same kinetic energy as that of a boy of half his mass. The man speeds up by 2 ms^(-1) and the boy changes his speed by x m s^(-1) so that the kinetic energies of the boy and the man are again equal. Then x in m s^(-1) is

Answer»

1/2 
`2sqrt(2)`
`SQRT(2)`
`2`

SOLUTION :Let the MASS of man be m.
Therefore, mass of the BOY is `m/2`
As. `1/2 mv_1^2 = 1/2(m/2) v_2^2 :. v_1= (v_2)/(sqrt2)`
`1/2 m(v_1 + 2)^2 = 1/2[m/2 (v_2 + X)^2]`
`:. (v_1 + 2)^2 = ((v_2 + x)^2)/(2) " or " v_1 + 2 = (v_2+ x)/(sqrt2)`
But `v_1 = (v_2)/(sqrt2) :. x/(sqrt2) = 2 " or " x = 2sqrt(2)`.
Discussion