Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

44501.

Show that the magnetic field at any point on the axis of the solenoid having n turns per unit length is B =(1)/(2) mu_(0) n I (cos theta_(1) - cos theta_(2)).

Answer»

SOLUTION :Consider a solenoid havingradius R consistsof n NUMBER of TURNS PER unit length .
Let P be the pointat a distance. Xformthe origin of thesolenoid.
The current carrying element dx ata distance. xfromorigin andthe distance r from point p .
` r = sqrt(R^(2) + (x'- x)^(2))`
The magnetic field due to current carryingcircular coil along its axis is
`dB = mu_(0)/2 . (IR^(2))/r^(2) xx N `
where ` N= ndx `
then ` dB = mu_(0)/2.(nIR^(2))/r^(3) . dx `
`sin theta= R/ r `
` r = R cosec phi ` .....(1)
`tan phi = R/ (x' - x) `
` x - x= R cotphi `
` (dx)/(d phi) = R cosec^(2) phi `
` dx = R cosec^(2) phi d phi ` .....(2)
from above equation ,
`dB = mu_(0)/ 2 . (nIR^(2).R cosec ^(2) phi .d phi )/(R^(3) cosec ^(3) phi ) `
`dB = mu_(0)/2 . nI sin phi d phi `
Total magnetic field can be obtained by INTEGRATING
`B= (mu_(0) nI)/2 underset(phi_(1))overset(phi_(2)) int sin phi d phi `
` B = ( mu_(0)nI)/2 [ - cos phi ]_(phi_(1))^(phi_(2))`
`B = (mu_(0)nI)/2 ( cos phi_(1) - cos phi_(2))`
Discussion
44502.

A coil having an area 2 m^(2) is placed in a magnetic field which changes from 1 Wb m^(2)" to "4 Wb m^(2) in an interval of 2 s. The induced emf in the coil will be

Answer»

4V
3V
1.5 V
2V

Solution :Here `phi_(1)=B_(1)A=1 xx 2 =2WB, phi_(2)=B_(2)A =4 xx 2=8" Wb and t=2s"`
`|EPSI|=(phi_(2)-phi_(1))/t=(8-2)/2=3V`
Discussion
44503.

A charge Q is placed at each of the opposite corners of square. A chargeqis placed at each of the other two corners. If the net electrical force on Q is zero , then Q/q equals.

Answer»

`-1`
`1`
`-(1)/(sqrt(2))`
`-2sqrt(2)`

Solution :The charge ARRANGEMENT is shown in figure. Let side of square be `.l.then AC =lsqrt2`
As force `oversetto (F_(AC))` is repulsive HENCE for equilibrium `oversetto (F_(AB)) and oversetto (F_(AD))` must be attractive i.e.,q must be negative
As force`oversetto (F_(AC) ) ` is repulsive, hence for equilibrium `oversetto (F_(AB)) "and" oversetto (F_(AD)) ` must be attractive i.e.,q must be negative
` ""|oversetto ( F_(AC)) | = ( kQ^(2))/((lsqrt2)^(2)) =(kQ^(2))/( 2L^(2)) and |oversetto (F_(AB))| = | oversetto (F_(AD)) |=(kQ .q)/(l^(2))`
Then ` ""|oversetto(F_(AB)) +oversetto (F_(AD))| =sqrt(F_(AB) ^(2) +F_(AD)^(2) )= ( sqrt2kQq)/(l^(2)) `
` (##U_LIK_SP_PHY_XII_C01_E04_014_S01.png" width="80%">
SINCE ` ""oversetto (F_(AC) ) +oversetto (F_(AB)) +oversetto (F_(AD)) =0, "hence" |oversetto (F_(AC)) | =- |oversetto (F_(AB))+oversetto (F_(AD)) | `
` THEREFORE "" (kQ^(2))/( 2l^(2)) =-(sqrt2kQq)/(l^(2)) rArr (Q)/(q) =-2sqrt2`
Discussion
44504.

Three identical, parallel conducting plates, A, B and C are placed as shwon. Switches S_(1) and S_(2) are open, and can connect A and C to earth when closed +Q charge is given to B.

Answer»

If `S_(1)` is closed with `S_(2)` OPEN a charge of amount `Q` will PASS THORUGH `S_(1)`
If `S_(2)` is closed with `S_(1)` open, a charge of amount `Q` will pass through `S_(2)`
If `S_(1)` and `S_(2)` are closed together, a charge of amount `Q//3` will pass through `S_(1)` and a charge of amount `2Q//3` will pass through `S_(2)`.
all the above statements are incorrect.

Answer :A::B::C
Discussion
44505.

block of mass 0-1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the mass is 0.5, the magnitude of the frictional force acting on the block is :

Answer»

0.98 N
0.49 N
4.9 N
2.5 N

Solution :Force of limiting FRICTION
`F_(f)= muR = 0.5 xx 5 = 2.5 N`
` wt. of block = mg = 0.1 xx 9.8 = 0.98N`
As weight is less than limiting friction ::. block does not move
:. FRICTIONAL force = wt. of block = 0.98 N

Hence correct CHOICE is (a).
Discussion
44506.

A : If white light is used is Young.s experimened the central bright fringe is white and the fringe closest on either side of the central white fringe is red. R : When white light is used in Y.D.S.E for a point .P. for which S_(2)S-S_(1)P= (lambda_B)/(2), (lambda_(B)=" wavelength of blue ") the blue component will be absent and fringe will appear red in colour.

Answer»

Both A and R are true and R is the CORRECT explanation of A
Both A and R are true and R is not the correct explanation of A
A is true and R is false
Both A and R are false

Answer :A
Discussion
44507.

A transformer is used to light a 100 W 110V lamp from a 220 V mains. If the main current is 0.5A, the effciency of the transfomer is approximately

Answer»

0.1
0.3
0.5
0.9

Answer :D
Discussion
44508.

Describewith suitableblock diagrams,action of pn-junctiondioide under forwardand reversebias conditions . Also draw I-V characteristics .

Answer»

Solution :FORWARD Bias :When a battery is connectedacross the junctionsuch that p side is connectedto the positiveterminaland n sideto thenegativeterminalof the source,the p-n junctionis said to be forwardbiased . The appliedvoltageopposesthe junctionp.d. and forvalues of the applied voltage GREATER than the junctionand constitutesa currentin an externalcircuit.This currentriseslinearlywith the appliedvoltagebeyondthe knee voltage . Thus a forward biasedp-n junctionoffers a low resistance.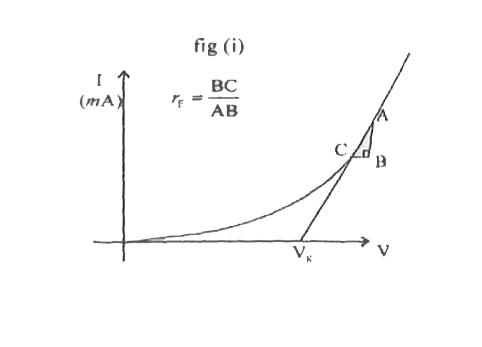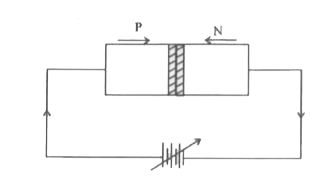


Reverse bias : When batteryis connected acrossthe junctionsuch that p side is connectedto the negative terminaland n side to the positive terminal , the p-n junction is said to be reverse biased In this case , the appliedvoltage adds to the EFFECT of junction p.d.and hencemajority carrierscannot cross the junction.The currentthroughthe circuit is practically zero.Thus ,reveres bias offersa very highresistancebut small CURRENT of the order of a few mA flowsthrough the circuit due to the minoritycarriersin the p and nregions. As the appliedvoltageis graduallyincreaseda very large currentresultsat a particularvoltage . This voltage is CALLED thebreak down or cut-in voltage.
Discussion
44509.

For a medium with permittivity and permeability mu, the velocity of light is given by :

Answer»

`SQRT(mu/EPSILON)`
`sqrt(muepsilon)`
`(1)/sqrt(muepsilon)`
`sqrt((epsilon)/mu)`

ANSWER :C
Discussion
44510.

Find the effective capacitance between the terminals a and b shown in figure.

Answer»

`(8C )/(27)`
`(26C )/(7 )`
`( 36C )/(7)`
`(19 C ) /(7)`

ANSWER :C
Discussion
44511.

Find the effective capacitance between the terminals a and b shown in figure.

Answer»

`(4C )/(3) `
`(C )/(3 ) `
`(2C )/( 3) `
`(5C )/(3)`

ANSWER :A
Discussion
44512.

The head lights of a jeep are 1.2 m apart. If the pupil of the eye of an observer has a diameter of 2 mm and light of wavelength 5896 Å, is used, what should be the maximum distance of the jeep from the observer if the two head lights are just separated ?

Answer»

`33.4` KM
`33.4` m
`3.34` km
`3.34` m

Solution :DISTANCE of JEEP, `X=(Dxxd)/(1.22xxlambda)`
D= Diameter of lens, d = Separation between sources
or `x=((2xx10^(-3))xx1.2)/(1.22xx5896xx10^(-10))m=3.34xx10^(3)m=3.34"km"`
Discussion
44513.

In the electrical network, shown in the diagram R_(1)=5Omega,R_(2)=2Omega,R_(3)=3Omega and E_(1)=2E_(2)=10V, sources have negligible internal resistance. For this network,

Answer»

The power generated in `R_(1)` is `6.4J//s`
if the sources of e.m.f. `E_(1)` and `E_(2)` were physically inter changed, without changing the polarities, the power generated in `R_(1)` will be the same.
If the polarities of the sources `E_(1)` and `E_(2)` were both reversed,the power generated in `R_(1)` will be the same.
The ratio of the power generated in `R_(2)` and `R_(3)` `1:30`

Solution :
(A). Power generated P is `R_(1)` is `i_(1)^(2)R_(1)` now `i_(1)=(V)/(R_(1))`
where V is the potential at `P`, ASSUMING that the negatives of the BATTERIES are earthed. Simple application of Kirchhoff's junction and loop laws
yields `i_(3)=(45)/(31)A,i_(2)=-(10)/(31)A`
`i_(1)=i_(2)+i_(3)=(35)/(31)A`
`V=R_(1)i_(1)=(175)/(31)=5.7V`
When `R_(1)=5Omega,R_(2)=2Omega,R_(3)=3Omega`
Hence `P=(V^(2))/(R_(1))=((5.7)^(2))/(5)=6.4(J)/(s)`
(B). CURRENT in `R_(1)` will be different if the sources of emf `E_(1)` and `E_(2)` are interchanged.
(C). Current in `R_(1)` will be reversed in direction but numerically be the same hence P is not changed
(D). Ratio of powers in `R_(2)` and `R_(3)` is given by
`(P_(2))/(P_(3))=((V-5)^(2)//R_(2))/((10-V)^(2)//R_(3))=((0.7)^(2)//2)/((4.3)^(2)//3)APPROX(1)/(30)`
Discussion
44514.

It is observed that only 0.39% of the originalradioactive sample remains undecayed after eight hours. Select the correct options.

Answer»

The HALF-life of that SUBSTANCE is 1 hour.
The mean life of the substance is `1/(ln 2)` hour.
Decay constant of the substance is ln 2 per hour.
If the number of radioactive nuclei of thissubstance at a given instant is `10^8` then the numberleft after 30 min would be `sqrt2xx10^7`

Solution :Here, t=8 hours
As `N=N_0 e^(-lambdat)` [ Law of radioactive decay]
`rArr N/N_0=e^(-lambdat) rArr 0.0039 =e^(-lambda8)`
`rArr e^(8lambda)=1/0.0039 = 256` or `e^(8lambda)=2^8`
Taking natural logarithm on both sides , we get
`8 lambda = 8 ln2`
`lambda` = ln2 per hour
Again, half life `=T_(1//2)=(ln2)/lambda`=1 hour
Mean time, `tau =1/lambda=1/(ln2)` hour
`therefore N=(10)^8 (1/2)^(1//2)=1/sqrt2xx10^8`
or `N=5sqrt2xx10^7` .
Discussion
44515.

One mole of a gas at standard temperatureand pressure (STP corresponds to 7=273 K and rho= 1.01 xx 10^5 Pa) occupies a volume of 22.5 /. Suppose the container is in the shape of a cube, (a) Determine the length of the cube edge, (b) What force is exerted by the gas on each face ofthe container ?

Answer»

SOLUTION :(a) 0.282 m, (B) 8.03 KN
Discussion
44516.

Same current l is flowing through 3 infinite long thin wires along+ve x,y,z axes. Find the net magnetic induction at a point (0,0,-a) such that yz plane is in the plane of the paper (i,jk are the unit vectors along x,y and z axes respectively)

Answer»

Solution :B due to conductor along Z-axis = 0
B due to conductor along y axis `vecB_(y)=(mu_(0))/(2PI)l/a(-HATI)`
B due to conductor along X-axis `vecB_(x)=(mu_(0))/(2pi)I/a(hatj)`
`(vecB("NET"))_(P)=vecB_(x)+vecB_(y)+vecB_(z)`
`=(mu_(0))/(2pi)I/a(-hati+hatj)`
Discussion
44517.

A parallel beamof light falls successively on a thin convex lens of focal length 40 cm and then ono a thini convex lens of focal length 10cm as shown in figure. In figure, the second lens is an equiconcave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm. Q. Now, a liquid of refractive index mu is filled to the right of the second lens in case B such that the area illuminated in both the cases is the same. Determing the refractive index of the liquid.

Answer»

1
2.5
3
1.5

Solution :In case (a), the incident parallel beam EMERGES as a parallel beam. So area ILLUMINATED,
`A_(1)=pi(1)^(2)=picm^(2)`
In case (b), let x be the diameter of the area illuminated.
Then,
`(x)/(45)=(1)/(5)rArr x=9cm`
`A_(2)=pi((9)/(2))^(2)=(81)/(4)picm^(2)`
`(A_(2))/(A_(1))=(81)/(4)`
When liquid of refractive index `mu` is filled to the right of this lens, the first surface of the lens (radius of curvature `=10cm)` forms the imag at the OBJECT only. Considering the refraction at the second surface.
`(mu)/(oo)-(1.5)/(-10)=(mu-1.5)/(10)` (therefore, same area `rArr upsilonrarroo)`
`rArr mu=3`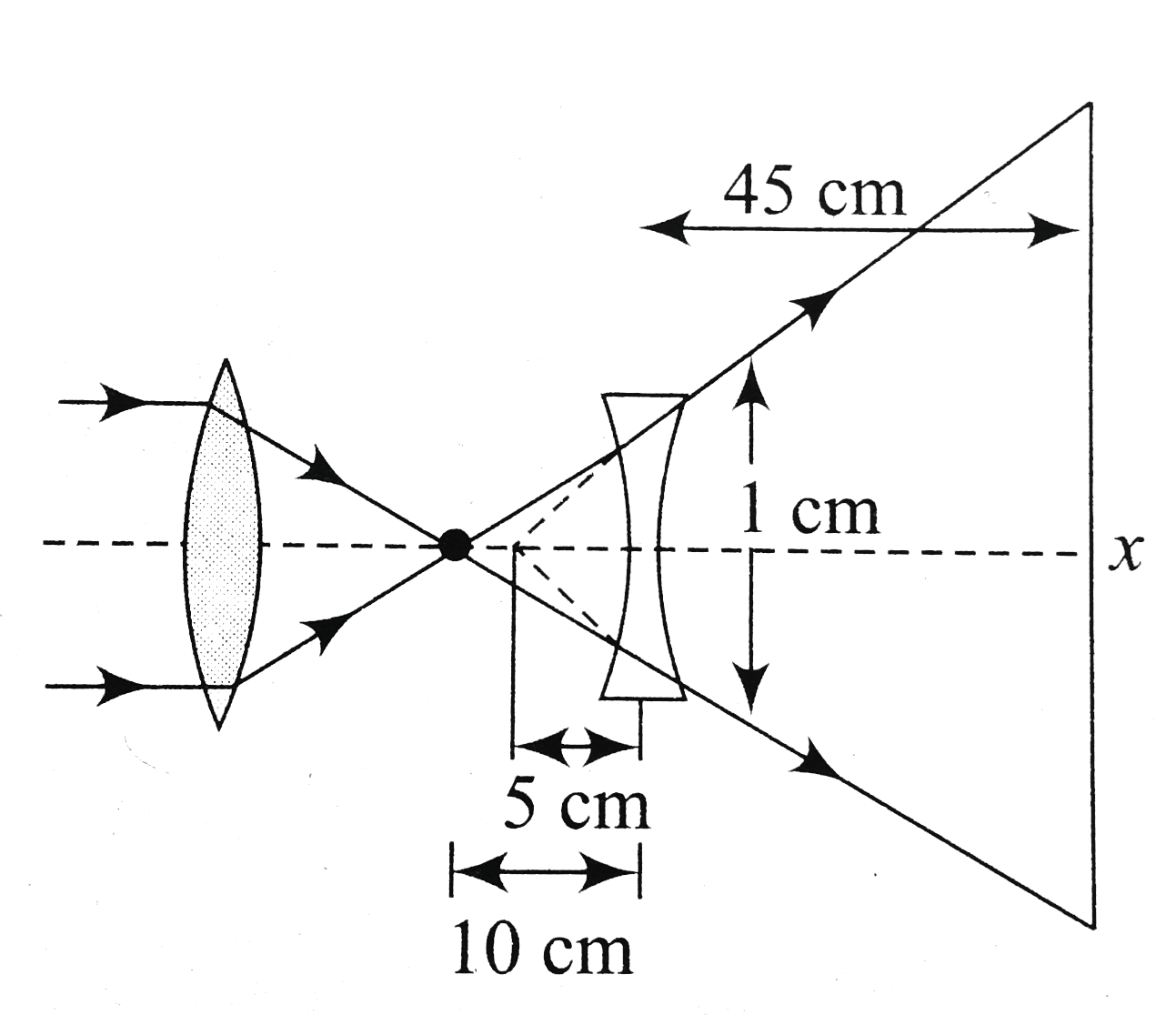
Discussion
44518.

A parallel beamof light falls successively on a thin convex lens of focal length 40 cm and then ono a thini convex lens of focal length 10cm as shown in figure. In figure, the second lens is an equiconcave lens of focal length 10cm and made of a material of refractive index 1.5. In both the cases, the second lens has an aperture equal to 1cm. Q. Compare the area illuminatedby the beam of light on the screen, which passes through the second lens in the two cases. The ratio (A_(2)//A_(1))will be

Answer»

`72//5`
`81//4`
`56//3`
`29//2`

Solution : In case (a), the incident parallel beam emerges as a parallel beam. So area illuminated,
`A_(1)=pi(1)^(2)=picm^(2)`
In case (b), let X be the diameter of the area illuminated.
Then,
`(x)/(45)=(1)/(5)rArr x=9cm`
`A_(2)=pi((9)/(2))^(2)=(81)/(4)picm^(2)`
`(A_(2))/(A_(1))=(81)/(4)`
When liquid of refractive index `mu` is FILLED to the right of this lens, the first surface of the lens (radius of curvature `=10cm)` forms the IMAG at the OBJECT only. Considering the refraction at the second surface.
`(mu)/(oo)-(1.5)/(-10)=(mu-1.5)/(10)` (therefore, same area `rArr upsilonrarroo)`
`rArr mu=3`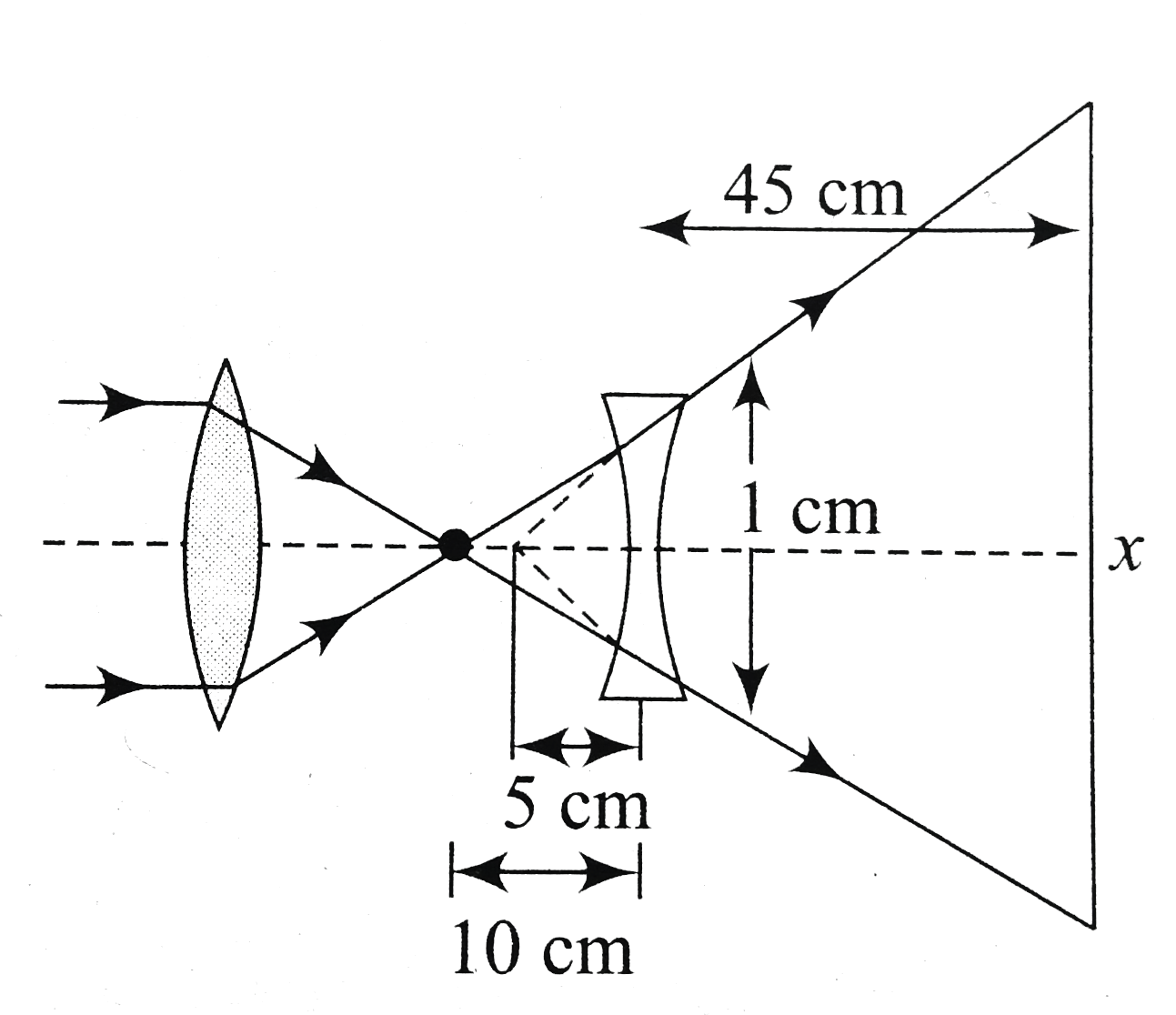
Discussion
44519.

The magnifying power of an astronomical telescope in the normal adjustment position is 100. The distance between the objective and the eyepiece is 101 cm. Calculate the focal length of the objective and the eyepiece.

Answer»

SOLUTION :Here, `|m| =f_(0)/f_(e) = 100rArr f_(0) = 100 f_(e)`
and `f_(0) + f_(e) =101 cm` or `100f_(e) + f_(e) = 101 f_(e) = 101 cm`
`RARR f_(e)= 1CM` and `f_(0) = 100 cm = 1 cm`
Discussion
44520.

A light ray is normally incident on one face of equilateral glass prism of refractive index sqrt2. Thedeviation of light ray is

Answer»

`30^@`
`45^@`
`60^@`
`75^@`

ANSWER :C
Discussion
44521.

When n-P-n transistor is used as an amplifier

Answer»

ELECTRONS move from EMITTER to COLLECTOR
Holes move from emitter to BASE
Electrons move from collector to base
Holes move from base to collector.

Answer :A
Discussion
44522.

A ray of light is incident at 50^(@) on the middle of one of the two mirros arranged at an angle of 60^(@) between them. The ray then touches the second mirror, making an angle of incidence of

Answer»

`50^(@)`
`60^(@)`
`70^(@)`
`80^(@)`

Solution :(c ) LET required angle be `THETA`

From geometry of FIGURE
In `Delta ABC , alpha = 180^(@) - (60^(@) + 40^(@)) = 80^(@)`
`rArr beta = 90^(@) - 80^(@) = 10^(@)`
In `Delta ABD , angle A = 60^(@), angle B = (alpha = 2 beta)`
`=(80 + 2 xx 10) = 100^(@) and angle D = (90^(@) - theta)`
`therefore angleA + angle B + angle D = 180^(@) rArr 60^(@) + 100^(@) + (90^(@) - theta)`
` = 180^(@) rArr theta = 70^(@)`.
Discussion
44523.

When two waves of interfering with each other have amplitudes aplha_1 and alpha_2 and the phase difference of 3pi, the resultant amplitude is :

Answer»

`a_1-a_2`
`(a_1)/a_2`
`(a_2)/a_1`
`(a_1+a_2)/(a_1-a_2)`

ANSWER :A
Discussion
44524.

Derive the law of reflection of light on the basis of Huygens wave theory.

Answer»

Solution :Law of REFLECTION :
(i) The incident wavefront AB, the reflected wavefront CD and the reflecting surface XY all the in the same plane.
(ii) Angle of INCIDENCE `i=/_PAN=90^(@)-/_NAB=/_BAC`
Angle of reflection `r=/_NAD=90^(@)-/_DAC=/_DCA`
In right angled TRIANGLES ABC and ADC
`/_B=/_D=90^(@)`

`BC=AD` and AC is common
`:.` The TWO triangles are congruent
`:./_BAC=/_DCA`
i.e., `i=r`
THUS the angle of incidence is equal to angle of reflection.
Discussion
44525.

The correct functinal group X and the reagent/reaction conditions Y in the following scheme are : Condenasation polymer formed Nylon-66

Answer»

`X=COOCH_(3), Y=H_(2)//NI//"heat"`
`X=CONH_(2),Y=H_(2)//Ni//"heat"`
` X=CONH_(2), Y=Br_(2)//NAOH`
` X=CN, Y=H_(2)//Ni//"heat"`

Solution :
Discussion
44526.

The energy band gap between valence band and conduction band is maximum in

Answer»

METALS.
super conductors.
semiconductors.
insulators.

Solution :Energy band GAP `E_(G)` is maximum for insulators having a value `E_(g) GT ` 3 eV.
Discussion
44527.

Electromagnetic waves propagate through free space or a medium as transverse waves. The electric and magnetic fields are perpendicular to each other as well as perpendicular to the direction of propagation of waves at each point. In the direction of wave propagation, electric field vecE and magnetic field vecB form a right-handed cartesian coordinate system. During the propagation of electromagnetic wave, total energy of electromagnetic wave is distributed equally between electric and magnetic fields. Since in_0 and mu_0 are permittivity and permeability of free space, the velocity of electromagnetic wave, c=(in_0 mu_0)^(-1//2). Energy density i.e., energy in unit volume due to electric field at any point, u_E=1/2in_0E^2 Similarly, energy density due to magnetic field , u_M=1/(2mu_0)B^2. If the electromagnetic wave propagates along x-direction, then the equations of electric and magnetic field are respectively. E=E_0sin(omegat-kx) and B=B_0sin(omegat-kx) Here, the frequency and the wavelength of oscillating electric and magnetic fields are f=omega/(2pi) and lambda=(2pi)/k respectively. Thus E_"rms"=E_0/sqrt2 and B_"rms"=B_0/sqrt2, where E_0/B_0=c. Therefore, average energy density baru_E=1/2in_0E_"rms"^2and baru_M=1/(2mu_0)B_"rms"^2. The intensity of the electromagnetic wave at a point, I=cbaru=c(baru_E+baru_B). To answer the following questions , we assume that in case of propagation of electromagnetic wave through free space, c=3xx10^8 m.s^(-1) and mu_0=4pixx10^(-7) H.m^(-1) If the electromagnetic wave propagates along x-axis, then the electric field vecE will be

Answer»

ALONG y-axis
along z-axis
on xy-plane
on yz-plane

Answer :D
Discussion
44528.

What do you mean by internal resistance of a cell ?

Answer»

Solution :The resistance offered by the electrolyte of a CELL to the flow of current between its ELECTRODES is called INTERNAL resistance of the cell.
An ideal battery has zero internal resistance and the potential difference across the batteryequals to its emf. But a real battery is made of electrodes and electrolyte, there is resistance to the flow of charges within the battery. A FRESHLY prepared cell has low internal resistance and it increases with AGEING.
Discussion
44529.

A compass needle made of pure iron (with density 8000 kg//m^2) has a length 5 cm, width 1.0 mm and thickness 0.50 mm. The magnitude of magnetic dipole moment of an iron is mu_"Fe"=2 xx 10^(-23) J/T. If magnetisation of needle is equivalent to the alignment of 10% of the atoms in the needle, what is the magnitude of the neddle's magnetic dipole momentmu ? (mass of iron per mole =0.05 kg//"mole", N_A=6xx10^23)

Answer»

`2.4xx10^(-3)` J/T
`4.8xx10^(-3) `J/T
`7.2xx10^(-3)` J/T
`9.6xx10^(-8)` J/T

Answer :B
Discussion
44530.

One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8 N. Let us consider the length of the rope to be along X-axis. A sample harmonic oscillator at x = 0 generates a transverse wave of frequency 100 Hz and amplitude 2 cm along the rope. Mass of a unit length of the rope is 20 gm/m. Ignoring the effect of gravity, answer the following questionsAssuming that the oscillator has its maximum negative displacement at t = 0, wave equation (function)for the wave can be expressed as

Answer»

`y = (0.02m) cos[ 8pi (RAD // m) x - 100pi (rad // s) t]`
` y = (0.02m) cos[ 10PI (rad // m) x - 200PI (rad // s) t]`
`y = (0.02m) cos[10pi (rad // m) x - 200pi (rad // s) t-pi]`
` y = -(0.02m) SIN[8pi (rad /x m) x - 100pi (rad // s) t]`

Answer :C
Discussion
44531.

Name the e.m. waves used for studying crystal structure of solids. What is its frequency range ?

Answer»

SOLUTION :X-rays. Frequency RANGE of X-rays is from `10^(16)Hz" to "10^(21)Hz`.
Discussion
44532.

One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8 N. Let us consider the length of the rope to be along X-axis. A sample harmonic oscillator at x = 0 generates a transverse wave of frequency 100 Hz and amplitude 2 cm along the rope. Mass of a unit length of the rope is 20 gm/m. Ignoring the effect of gravity, answer the following questionsWavelength of the wave is

Answer»

50cm
20cm
8cm
32cm

Answer :B
Discussion
44533.

In a wheatstone's bridge arrangement we can interchange the cell and galvanometer without affecting the balance condition of the bridge.

Answer»

SOLUTION :TRUE
Discussion
44534.

The current gain of an n-p-n transistor in common emitter configuration is 100. What will be the change in the emitter current, if the collector current changes by 1mA?

Answer»

`1.00mA`
`0.99mA`
`1.01mA`
`1.5mA`

ANSWER :C
Discussion
44535.

Th equivalent resistance between points A and B of an infinite network of resistance each of 1Omegaconnected as shown is

Answer»

inifinite
`2 OMEGA `
ZERO
`((1 + SQRT(5))/( 2))`

Answer :D
Discussion
44536.

Electromagnetic waves propagate through free space or a medium as transverse waves. The electric and magnetic fields are perpendicular to each other as well as perpendicular to the direction of propagation of waves at each point. In the direction of wave propagation, electric field vecE and magnetic field vecB form a right-handed cartesian coordinate system. During the propagation of electromagnetic wave, total energy of electromagnetic wave is distributed equally between electric and magnetic fields. Since in_0 and mu_0 are permittivity and permeability of free space, the velocity of electromagnetic wave, c=(in_0 mu_0)^(-1//2). Energy density i.e., energy in unit volume due to electric field at any point, u_E=1/2in_0E^2 Similarly, energy density due to magnetic field , u_M=1/(2mu_0)B^2. If the electromagnetic wave propagates along x-direction, then the equations of electric and magnetic field are respectively. E=E_0sin(omegat-kx) and B=B_0sin(omegat-kx) Here, the frequency and the wavelength of oscillating electric and magnetic fields are f=omega/(2pi) and lambda=(2pi)/k respectively. Thus E_"rms"=E_0/sqrt2 and B_"rms"=B_0/sqrt2, where E_0/B_0=c. Therefore, average energy density baru_E=1/2in_0E_"rms"^2and baru_M=1/(2mu_0)B_"rms"^2. The intensity of the electromagnetic wave at a point, I=cbaru=c(baru_E+baru_B). To answer the following questions , we assume that in case of propagation of electromagnetic wave through free space, c=3xx10^8 m.s^(-1) and mu_0=4pixx10^(-7) H.m^(-1) Average energy density (in J . m^(-3))of electromagnetic wave at that point

Answer»

`4.98xx10^(-9)`
`9.95xx10^(-9)`
`4.98xx10^(-10)`
`9.95xx10^(-10)`

ANSWER :D
Discussion
44537.

An X-ray tube operates on 30 kV. The minimum wavelength emitted is h = 6.6 xx 10^(-34) Js, c = 3 xx 10^(8) m/s, e = 1.6 xx 10^(-19)C.

Answer»

6.6 `Å`
0.133 `Å`
1.2 `Å`
0.4 `Å`

SOLUTION :`lambda_(min) = (hc)/(eV) = (6.6 xx 10^(-34) xx 3 xx 10^(8))/(1.6 xx 10^(-19) xx 30 xx 10^(3)) m = 0.4 xx 10^(-10) m = 0.4 Å`
Discussion
44538.

Assertion If a glass slab is placed in front of one of the slits, then fringe width will decrease Reason Glass slab will produce an additional path difference.

Answer»


Solution :FRINGE width does not CHANGE by the INTRODUCTION of GLASS slab
Discussion
44539.

Electromagnetic waves propagate through free space or a medium as transverse waves. The electric and magnetic fields are perpendicular to each other as well as perpendicular to the direction of propagation of waves at each point. In the direction of wave propagation, electric field vecE and magnetic field vecB form a right-handed cartesian coordinate system. During the propagation of electromagnetic wave, total energy of electromagnetic wave is distributed equally between electric and magnetic fields. Since in_0 and mu_0 are permittivity and permeability of free space, the velocity of electromagnetic wave, c=(in_0 mu_0)^(-1//2). Energy density i.e., energy in unit volume due to electric field at any point, u_E=1/2in_0E^2 Similarly, energy density due to magnetic field , u_M=1/(2mu_0)B^2. If the electromagnetic wave propagates along x-direction, then the equations of electric and magnetic field are respectively. E=E_0sin(omegat-kx) and B=B_0sin(omegat-kx) Here, the frequency and the wavelength of oscillating electric and magnetic fields are f=omega/(2pi) and lambda=(2pi)/k respectively. Thus E_"rms"=E_0/sqrt2 and B_"rms"=B_0/sqrt2, where E_0/B_0=c. Therefore, average energy density baru_E=1/2in_0E_"rms"^2and baru_M=1/(2mu_0)B_"rms"^2. The intensity of the electromagnetic wave at a point, I=cbaru=c(baru_E+baru_B). To answer the following questions , we assume that in case of propagation of electromagnetic wave through free space, c=3xx10^8 m.s^(-1) and mu_0=4pixx10^(-7) H.m^(-1) The peak value of magnetic field (in Wb . m^(-2)) at that point

Answer»

`5XX10^(-8)`
`45xx10^(-8)`
`5xx10^8`
`45xx10^8`

ANSWER :A
Discussion
44540.

One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8 N. Let us consider the length of the rope to be along X-axis. A sample harmonic oscillator at x = 0 generates a transverse wave of frequency 100 Hz and amplitude 2 cm along the rope. Mass of a unit length of the rope is 20 gm/m. Ignoring the effect of gravity, answer the following questionsTension in the given rope remaining the same, if a simple harmonic oscillator of frequency 200 Hzis used instead of the earlier oscillator of frequency 100 Hz, then

Answer»

speed of transverse WAVES in the rope will be doubled, wavelength will not change
speed of transverse waves in the rope will become HALF, wavelength will become one-fourth
speed of transverse waves in the rope will become FOUR times, wavelength will be doubled
speed of transverse waves in the rope will not change, wavelength will become half

Answer :D
Discussion
44541.

Distinguish between 'Analog and Digital signals'.

Answer»

Solution :Analog Signal : The amplitude of the signal VARIES continuously with time. The value of the signal at any instant is REPRESENTED by its amplitude at that instant. For example, pressure variation in the SOUND waves can be converted into CORRESPONDING current or voltage variations with the help of a microphone.
Digital Signal : In a digital signal, the amplitude of the signal is discontinuous with time. The amplitude of a digital signal has only two levels i.e., either low or high. Thus, a digital signal in the form of pulses usually uniformly speed in time.
Discussion
44542.

Small drops of the same sizes are charged to V volt each. If x such drops coalesce to farm a single large drop, i^ potential will be:

Answer»

VN
`V/n`
`Vn^(1/3)`
`Vn^(2/3)`

ANSWER :D
Discussion
44543.

The focal lengths of a thin lens for red and violetlight are 90.0 cm and 86.4cm respectively. Find the dispersive power of the material of the lens. Make appropriate assumptons.

Answer»

Solution :We have
`(1)/(F) = (mu-1) ((1)/(R_1) - (1)/(R_2))`
`or `mu - 1 = (1)/(f). (1)/((1)/(R_1) - (1)/(R_2)) = (K)/(f).`
THUS, `mu_(upsilon) -1 = (K)/(f_(upsilon))`
and `mu_r - 1=(K)/(f_r)`
so that `mu_(upsilon) - mu_r = K((1)/(f_(upsilon)) - (1)/(f_r))`
`=K[(1)/(85.4 cm) - (1)/(90CM)]=Kxx4.6 XX 10^(-4) cm^(-1)`
Also, we can assume that
`mu_y -1 = (mu_(upsilon) + mu_r)/(2) -1 = (mu_(upsilon) - 1)/(2) + (mu_(upsilon)-1)/(2)`
`(K)/(2) ((1)/(f_(upsilon) + (1)/(f_r))`
`=(K)/(2) [(1)/(86.4 cm) + (1)/(90cm)] = Kxx1.1xx10^(-2)cm^O(-1)`
Thus, the dispervise power of the meterial of the lens
`omega= (mu_(upsilon) - mu_r)/(mu_y - 1) = (4.6xx 10^(-4))/(1.1xx10^(-2)) = 0.042.`
Discussion
44544.

(a) Calcualte the potential at a point P due to a charge of 4 xx 10^(-7) C located 9 cm away. (b) Hence obtain the work done in bringing a charge of 2 xx 10^(-9) C from infinity to the point P. Does the answer depend on the path along which the charge is brought?

Answer»

Solution :(a) `V= 1/(4piepsilon_(0)). Q/r = 9 xx 10^(9)Nm^(2)C^(-2) xx (4 xx 10^(-7) C)/(0.09m)`
`=4 xx 10^(4)` V
(B) `W = qV = 2 xx 10^(-9) C xx 4 xx 10^(4)` V
`= 8 xx 10^(-5)` J
No, work DONE will be path independent. Any arbitrary infinitesimal path can be resolved into two perpendicular displacements. One along r and another perpendicular to r. The work done corresponding to the later will be zero.
Discussion
44545.

One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8 N. Let us consider the length of the rope to be along X-axis. A sample harmonic oscillator at x = 0 generates a transverse wave of frequency 100 Hz and amplitude 2 cm along the rope. Mass of a unit length of the rope is 20 gm/m. Ignoring the effect of gravity, answer the following questionsMaximum magnitude of transverse acceleration of any point on the rope will be nearly

Answer»

`7888 m//s^2`
`8244 m//s^2`
`9277 m//s^2`
`3333 m//s^2`

ANSWER :A
Discussion
44546.

One end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8 N. Let us consider the length of the rope to be along X-axis. A sample harmonic oscillator at x = 0 generates a transverse wave of frequency 100 Hz and amplitude 2 cm along the rope. Mass of a unit length of the rope is 20 gm/m. Ignoring the effect of gravity, answer the following questionsWhich of the following is correct ?

Answer»

The wave propagates with a fixed and any PARTICLE of the MEDIUM vibrates with the same fixed SPEED
The wave propagates with a fixed speed but any particle of the medium vibrates with a variablespeed
The wave propagates with a variable speed but any particle of the medium vibrates with some fixed speed
The wave propagates with a variable speed and any particle of the medium ALSO vibrates with a variable speed

Answer :B
Discussion
44547.

Electromagnetic waves propagate through free space or a medium as transverse waves. The electric and magnetic fields are perpendicular to each other as well as perpendicular to the direction of propagation of waves at each point. In the direction of wave propagation, electric field vecE and magnetic field vecB form a right-handed cartesian coordinate system. During the propagation of electromagnetic wave, total energy of electromagnetic wave is distributed equally between electric and magnetic fields. Since in_0 and mu_0 are permittivity and permeability of free space, the velocity of electromagnetic wave, c=(in_0 mu_0)^(-1//2). Energy density i.e., energy in unit volume due to electric field at any point, u_E=1/2in_0E^2 Similarly, energy density due to magnetic field , u_M=1/(2mu_0)B^2. If the electromagnetic wave propagates along x-direction, then the equations of electric and magnetic field are respectively. E=E_0sin(omegat-kx) and B=B_0sin(omegat-kx) Here, the frequency and the wavelength of oscillating electric and magnetic fields are f=omega/(2pi) and lambda=(2pi)/k respectively. Thus E_"rms"=E_0/sqrt2 and B_"rms"=B_0/sqrt2, where E_0/B_0=c. Therefore, average energy density baru_E=1/2in_0E_"rms"^2and baru_M=1/(2mu_0)B_"rms"^2. The intensity of the electromagnetic wave at a point, I=cbaru=c(baru_E+baru_B). To answer the following questions , we assume that in case of propagation of electromagnetic wave through free space, c=3xx10^8 m.s^(-1) and mu_0=4pixx10^(-7) H.m^(-1) Intensity (in W . m^(-2)) of electromagnetic wave at that point is almost

Answer»

0.15
0.3
0.45
0.6

Answer :B
Discussion
44548.

Two identical conducting spheres, fixed in place, attract each other with an electrostatic force of 0.108 N when their center-to-center separation is 50.0 cm. The spheres are then connected by a thin conducting wire. When the wire is removed, the spheres repel each other with an electrostatic force of 0.144 N. Of the initial charges on the spheres, with a positive net charge, what was (a) the negative charge on one of them and (b) the positive charge on the other ?

Answer»

SOLUTION :(a) `-0.646 MU C`, (B) `4.65 mu C`
Discussion
44549.

How are rainbows formed?

Answer»

SOLUTION :(i) Rainbow is due to dispersion of sunlight through droplets of water during rainy days.
(ii) When sunlight FALLS on the water drop suspended in air, it splits (or dispersed) into its CONSTITUENT seven colours. Thus, water drop suspended in air behaves as a glass prism.
(iii) Primary rainbow is FORMED when light entering the drop undergoes one total internal reflection inside the drop before coming out from the drop.
(iv) The angle of view for violet to red in primary rainbow is `40^@`to `42^@`. A secondary rainbow appears outside of a primary rainbow and develops when light entering a raindrop undergoes two internal reflections. The angle of view for red toviolet in a secondary rainbow is, `52^@` to `54^@.`
Discussion
44550.

The average binding energy per nucleon for the nuclei lying in the middle of periodic table, mass number 'A' ranging from 40 to 120, is nearly ..............

Answer»

SOLUTION :8.5MeV PER NUCLEON
Discussion