Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 42951. |
An ice ball of radius a and mass m is placed at 0^@C inside a thick hollow sphere of inner and outer radii a and b whose thermal conductivity varies as k=alpha/r^2, where alpha is a positive constantand r is the distance from centre. The temperature of surrounding is theta_0 and latent heat of fusion for ice is L_f.Then ,time required to completely melt the ice ball is (Neglect the contraction in volume when ice melts into water and any change in thermal resistance due to melting of ice of the system.) |
|
Answer» `(mL_f LN (b/a))/(4pialpha theta_0)` |
|
| 42952. |
Energy of an etectron in och orbit of hydrogen atom is k=(1)/(4pi epsi_(0)) |
|
Answer» `-(2PI^(2)k^(2) me^(4))/(N^(2) h^(2))` |
|
| 42953. |
A target is made of two plates, one of wood and the other of iron. The thickness of the wooden plate is 4 cm and that of iron plate is 2 cm. A bullet fired goes through the woodfirst and then penetrates 1 cm into iron. A similar bullet fired with the same velocity from opposite direction goes through ironfirst and then penetrates 2 cm into wood. If a_(1) and a_(2) be the retardations offered to the bullet by wood and iron plates, respectively, then |
|
Answer» `a_(1)=2a_(2)` |
|
| 42954. |
Calculate the tension in the thread during equilibrium condition(m=80×10^(-6)kg, q=2×10^(-8)C) - |
|
Answer» 8.8 N  during equilibrium `T cos theta = MG` `T sin theta = qE` `T = sqrt((mg)^(2)+(qE)^(2))` `T= sqrt((80xx10xx10^(-6))^(2)+(2xx10^(-8) xx 2 xx 10^(4))^(2))` `T= sqrt(64 xx 10^(-8) +16 xx 10^(-8))` `T= sqrt(80 xx 10^(-8)) = 8.8 xx 10^(-4)N` |
|
| 42955. |
The wavelength of photon is proportional to (where upsilon = fequency) |
|
Answer» `UPSILON` |
|
| 42956. |
Answer the following questions: (b) A virtual image, we always say, cannot be caught on a screen. Yet when we 'see' a virtual image, we are obviously bringing it on to the 'screen' (i.e., the retina) of our eye. Is there a contradiction? |
| Answer» Solution :(b) When the REFLECTED or refracted RAYS are divergent, the image is virtual. The divergent rays can be converged on to a screen by means of an appropriate converging lens. The convex lens of the eye does just that. The virtual image here SERVES as an object for the lens to PRODUCE a real image. Note, the screen here is not LOCATED at the position of the virtual image. There is no contradiction. | |
| 42957. |
A 6V cell with 0.5 Omegainternal resistance and 10 V cell with 1 Omegainternal resistance and a 12 Omegaexternal resistance are connected in parallel. The current in amp through the 10 V cell is |
|
Answer» `0.6` |
|
| 42958. |
Which of the following logic gates in a universal gate? |
|
Answer» OR |
|
| 42959. |
Give definition and formula of root mean square plot graph of current versus omega t. |
|
Answer» Solution :Root mean square of any physical quantity is called root mean square. In short rms or it is also called effective quatity. rms current is denoted by I or `I_(rms)` . The graphsof I versus of `omega t ` is given below.  The rms current is related to peak current `I_(m)` by`I = ( I_(m))/( sqrt(2)) = 0.707 I_(m)` `I_(rms) = sqrt( lt I^(2) GT )` `= sqrt((1)/(2) I_(m)^(2))` `= ( I_(m))/( sqrt(2)) = 0.707 I_(m)` Formula of rms for average POWER. `P = bar(p) = ( 1)/(2) I_(m)^(2) R = I_(rms) ^(2) R [ :. (1)/(2) I_(m)^(2) = I_(rms)^(2)]` and rms VALUE for voltage, `V = ( V_(m))/( sqrt(2)) = 0.707V_(m)` Now `V_(m) =I_(m)R ` or `(V_(m))/( sqrt(2)) = ( I_(m))/( sqrt(2)) R` or `V = IR `. These equations shows the relation between AC voltage and ac current. For DC voltage relation is given by `P = (V^(2))/( R ) = VI = I^(2) R ` |
|
| 42960. |
A man of mass 60 kg sitting on ice pushes a block of mass of 12kg on ice horizontally with a speed of 5 ms^(-1). The coefficient of friction between the man and ice and between block and ice is 0.2. If g =10 ms^(-2), the distances between man and the block, when they come to rest is |
| Answer» ANSWER :B | |
| 42961. |
In Young's experiment if mica disc of thickness t and refractive index is placed in the path of one ray coming out of slit, fringes will move ...... distance on the screen |
|
Answer» `(d)/(D)(mu-1)t` But phase difference `=(xd)/(D)` `:. (n-1)=t=(xd)/(D)` `:.x()/(D)(n-1)t` `:.` Frings will MOVE distance `(D)/(d)(mu-1)t`. |
|
| 42962. |
If the tempurature of a good conductor increases, how does the relaxation time of electron in the conductor change ?. |
| Answer» SOLUTION :With increase in temperature, the electrons collide more frequently with positive metal ions. So, their relaxation TIME DECREASES. | |
| 42963. |
A boat radioed a distress call to a Coast Guard station. At the time of the call, a vector A from the station to the boat had a magnitude of 45.0 km and was directed 15.0^(@) east of north. A vector from the station to the point where the boat was later found is B = 30.0km 15.0^(@) north of east. How far did the boat travel from the point where the distress call was made to the point where the boat was found ? In other words, what is the magnitude of vector C ? |
|
Answer» `64.3km` |
|
| 42964. |
Determine the current in each branch of the network shown in figure. |
| Answer» Solution :CURRENT in branch AB = (4/17) A. In BC = (6/17) A , in CD = (-4/17) A, in AD =(6/17) A, in BD =(-2/17) A, total current =(10/17A) | |
| 42965. |
Atomic clock generally used in the national standards, is based on the periodic vibrations of period |
|
Answer» `pm 1 XX 10^(-13)` s |
|
| 42966. |
A double-layer cylindrical capacitor consists of conductors of radii R_(1) and R_(3) and two layers of dielectrics of relative permittivtties epsilon_(1) and espion_(2). The radius of the common surface of the dielectrics. Is R_(2) . The breakdown field strengths of the dielectrics are E_(1) and E_(2) respectively. What is the breakdown voltage of this capacitor if (a) epsilon_(1)R_(1)E_(1) lt epsilon_(2)R_(2)E_(2) (b)epsilon_(2)R_(2)E_(2)gtepsilon_(1)E_(1)R_(1)? [Hint: If E_(1)=E_(1max) and E_(2)gt ,E_(2max) dielectric 1 will break first and if E_(2)=E_(2max') E_(1) gt E_(1max) dielectric 2 will break first.] |
|
Answer» |
|
| 42967. |
A boat radioed a distress call to a Coast Guard station. At the time of the call, a vector A from the station to the boat had a magnitude of 45.0 km and was directed 15.0^(@) east of north. A vector from the station to the point where the boat was later found is B = 30.0km 15.0^(@) north of east. What are the components of the vector from the point where the distress call was made to the point where the boat was found? In other words, what are the components of vector C = B-A ? |
|
Answer» |
|
| 42968. |
A p-n junction diode is said to be forward biased when a potential difference applied across p and n region makes |
|
Answer» <P>p-region POSITIVE and n-region NEGATIVE. |
|
| 42969. |
Consider a frictionless ramp on which a smooth object is made to slide down from an initial height 'h'. The distance 'd' necessary to stop the object on a flat track of coefficient of friction 'mu.'), kept at the ramp end is |
|
Answer» `H//MU` |
|
| 42970. |
Consider a compound slab consisting of two different materials having equal thickness and thermal conductivities K and 2 K respectively. The equivalent thermal conductivity of the slab is |
|
Answer» `2/3K` `K_(s)=(2K_(1)K_(2))/(K_(1)+K_(2))=(2K.2K)/(K+2K)=(4K^(2))/(3K)=(4)/(3)K`. Correct choice is (d). |
|
| 42971. |
A unit positive point charge of mass m is projected with a velocity v inside the tunnel as shown. The tunnel has been made inside a uniformly charged non-conducting sphere with charged density rho. The minimum velocity with which the point charge should be projeted such it can it reach the opposite end of the tunnel is equal to. |
|
Answer» `[RHOR^(2)//4mepsilon_(0)]^(1//2)` |
|
| 42972. |
Who is the poet of the poem? |
|
Answer» RABINDRANATH Balaji |
|
| 42973. |
A Diwali rocket is ejecting 0.05 kg of gases per second at a velocity of 200 m//s. The accelerating force on the rocket is : |
| Answer» Answer :A | |
| 42974. |
Find the apparent depth of a fish (in meter) whose real depth is 100m and is observed at an angle of vision 53^(@) as shown in the figure |
|
Answer» |
|
| 42975. |
A glass plate has a thicknes t and refractive index mu. The angle of incidence of a ray from air into the plate is equal to the critical angle for glass air intrerface. The lateral shift (perpendicular distance between incident ray and emergent ray) of ray is given by |
|
Answer» `t(1-1/(SQRT(MU^(2)+1)))` |
|
| 42976. |
The figure shows a long cylinder and its cross section. There are N (N is a large number) wire on the curved surface of the cylinder at uniform spacing and paral- lel to its axis. Each wire has current I and cross sectional radius of wires are small compared to radius R of the cyl- inder. Find magnetic field at a distance x from the axis of the cylinder for(a) x lt R (b) x gt R |
|
Answer» |
|
| 42977. |
The potential energy U of a body of mass m is given by U = ax + by where x and y are the position coordinates of the particle, the net force acting on the particle is: |
|
Answer» `sqrt(a^(2) +B^(2))` `F_(y)=(-dU)/(dy)impliesF_(y)=-b` :.`F=sqrt(F_(x)^(2)+F_(y)^(2))=sqrt(a^(2)+b^(2))` Hence correct CHOICE is (a). |
|
| 42978. |
Four blocks A, B, C and D of equal mass are placed on the belt of conveyor at equal distances as shown. Mass of each block is 2 kg and distance between blocks (d) is 400 mm. Assume masses of rollers and conveyor are negligible. Friction is sufficient to prevent the slipping between blocks and belt. A constant force of 1000 N is applied parallel to the belt as shown. Neglect the radius of roller as compare to d. The magnitude of velocity of block B when it leave the roller at point 'T' is 10sqrt((7)/(alpha))m//s. Find the value of alpha. |
|
Answer» |
|
| 42979. |
The condition in which the vectors vec P=3hati - 5 hatj + 5hatk and vec Q= 5hati - hatj + xhatk be perpendicular, then valus of x is |
| Answer» ANSWER :C | |
| 42980. |
A light rod of length 200 cm is suspended from the ceiling horizontally by means of two vertical wires of equallength tied to its ends. One of the wires is made of steel and is of cross- section0.1 cm^(2) and the other of brass of cross-section 0.2 cm^(2). Along the rod at which distance a weight may be hung to produce equal stresses in both the wires ? |
|
Answer» ` 4/3` m from steel wire  As stresses are EQUAL, ` T_(1)/A_(1) = T_(2)/A_(2)` ` i.e, T_(1)/T_(2) = A_(1)/A_(2)= (0.1)/(0.2) or T_(2) = 2T_(1)` Now fortranslatory EQUILIBRIUM of the rod, `T_(1) + T_(2) =W` From (i) and (ii) , we get ` T_(1) = W/3 , T_(2) = (2W)/3` Now if x is the distanceof weight W from steel wire, thenfor rotationalequilibriumof rod, ` T_(1)x = T_(2) (2 -x) or W/3 x = (2 W)/ 3 (2 -x) therefore x = 4/3 m` |
|
| 42981. |
In Fig. 6-44a, a sled is held on an inclined plane by a cord pulling directly up the plane. The sled is to be on the verge of moving up the plane. In Fig. 6-44h, the magnitude F required of the cord's force on the sled is plotted versus a range of values for the coefficient of static friction u between sled and plane: F_(1) 2.0 N, F_(2)= 5.0 N, and mu_(2) = 0.25. At what angle theta is the plane inclined? |
| Answer» SOLUTION :`9.5^(@)` | |
| 42982. |
From the top of a tower 40 m high a ball is projected upwards with a speed of 20 ms -1 at an angle 30° with the horizontal. The ratio of the total time of flight to hit the ground to the time taken by it to come back to the same initial elevation (g = 10 ms^(-2) ) is : |
|
Answer» `3:2` `T=(2usintheta)/g=(2xx20xx1/2)/10=2`sec Time taken to GO from C to D is `h=ut + 1/2g t^(2)`, INITIAL vertical velocity= `20sin30^@` `40=20xx1/2xxt +5t^(2)` `implies t^(2)+4t -2t-8=0` r(t + 4)-2(t + 4) = 0 (r + 4) (r-2) = 0 `implies` t = 2 s as time cannot be negative. 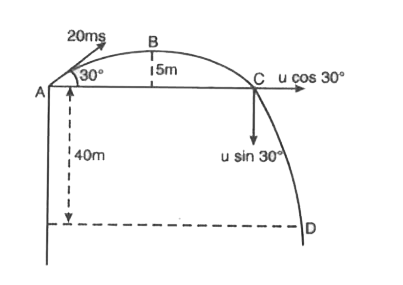 `:.` Time taken to go from A to D= 2+2=4s `:.` ratio of timings = `4/2=2:1` |
|
| 42983. |
What was strange about the old book? |
|
Answer» It was a computer. |
|
| 42984. |
Find out the value of x for which the image is formed on the object itself. |
|
Answer» Solution :Case I : for first Refraction `n_(2)/v-n_(1)/U=(n_(2)-n_(1))/R` `rArr 1.5/v+1/x=0.5/10` `rArr 1.5/v=0.5/10-1/x` `rArr 1.5/v=(0.5x-10)/(10x)` `rArr v=(15x)/(0.5x-10)` `v=oo` `rArr x=20` CM 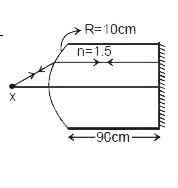 Case II : `n_(2)=1.5` `n_(1)=1` `R= +10` `u= -x` `v=90` cm `x=30` cm 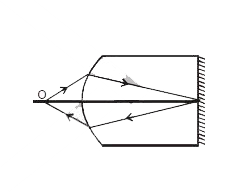
|
|
| 42985. |
The displacement y of a particle executing periodic motion is given by y = 4 cos^2 (1/2t) sin (1000t)This expression may be considered to be a result of the superposition of ............ independent harmonic motions |
|
Answer» TWO |
|
| 42986. |
A system consis of a ball of radius R carrying a spherically symmetric charge and the surrounding space filled with a charge of volume density rho = alpha//r where, alpha isa constant, r is the distance from the centre of the ball. Find the ball.s charge, at which the magnitude of the electric field strenght vectros is independent of r outside the ball. How high is this strenght? The permittivities of the ball and the surrounding space are assumed to be equal to unity. |
|
Answer» `q=piR^(2)ALPHA,E=alpha//epsilon_(0)` |
|
| 42987. |
Define power of lens. What is its unit? |
| Answer» Solution :Power of a LENS is the reciprocal of focal LENGTH, when F in METRES. Its UNIT is dioptre | |
| 42988. |
Find the energy per unit volume-of medium in an -electric field of intensity 100 volt/metre. Dielectric constant of medium = 3 |
| Answer» Solution :ENERGY density PER unit VOLUME `=1/2kepsilon_0E^2=1/2xx3xx8.85xx10^-12xx(100)^2=1.327xx10^-7J//m^3`. | |
| 42989. |
A molecule of a substance has a permanent electric dipole moment of magnitude 10^(-30) Cm. A mole of this substance is polarised (at low temperature) by applying a strong electrostatic field of magnitude 10^(7) vm^(-1). The direction of the field is suddenly changed by an angle of 60^(@). Estimate the heat released by the substance in aligning its dipole along the new direction of the field. For simplicity assume 100 % polarisation of the sample. 1 mole = 6 xx 10^(23) molecule. |
| Answer» SOLUTION :`DELTAU = 3J` | |
| 42990. |
The input signal given to a CE amplifier having a voltage gain of 150 is V_(i) = 2cos(15t+(pi)/(3)) The corresponding output signal will be |
|
Answer» `300cos(15t+(4pi)/(3))` |
|
| 42991. |
A stone falls frecly from rest and the total distance covered by it in the last second of its motion cquals the distance covered by it in the first three seconds of its motion. The stone remains in the air for |
|
Answer» 6S From s = ut`+(1)/(2) "GT"^(2)` Here `U =0 :. S =(1)/(2) "gt"^(2)` Total distance travelled by the stone inlast second is `D= s_(t) s_(t-1)=(1)/(2) "gt"^(2)-(1)/(2) g (t-1)^(2)= (g)/(2) (2t-1)` Distance travelled by the stone in first three seconds is `s_(3) =(1)/(2) xxgxx3^(2)=(9)/(2) g or 2t-1 =9` t=5s |
|
| 42992. |
Molten-wax of mass m drops on a block of mass M, which is oscillating on a frictionless table as shown. Select t he CORRECT statements. (i) If the collision takes place at extreme position, amplitude does not change (II) If the collision takes place at mean position, amplitude decreases (III) If the collision takes place at mean position, time period increases (IV) If the collision takes place at extreme position, time period increases |
|
Answer» Only (I), (II) If mass increases time period increases. If collision take place of extreme position then no energy loss take place HENCE AMPLITUDE remains same. If collision take place at mean position then due to inelastic collision energy loss take place & Amplitude decreases. |
|
| 42993. |
Neutron was discovered by the experiment of |
|
Answer» ARTIFICIAL transmutation of `(._4Be^9)`by `ALPHA` - PARTICLES |
|
| 42994. |
Determine the current in each branch of the given network. |
Answer» Solution : In above circuit, we have to find currents in different branches. Applying KVL in the closed path ABDA, `- 10I_(1) -5I_(3) + 5I_(2) = 0 ` `therefore 10 I_(1) = 5I_(2) - 5I_(3)` `therefore 2I_(1)= I_(2) - I_(3) ""` ... (1) Applying KVL in the closed path BCDB, ` - 5 (I_(1) - I_(3)) + 10 (I_(2) + I_(3)) + 5I_(3) = 0 ` `therefore 5I_(1) = 20I_(3) + 10I_(2)` `therefore I_(1) = 2I_(2) + 4I_(3)` `therefore 2I_(1) = 4I_(2) + 8I_(3) "" `.... (2) From equation (1) and (2), `I_(1) - I_(3) = 4I_(2) + 8I_(3)` `therefore 3I_(2) = - 9I_(3)` `therefore I_(2) = - 3I_(3) "" `... (3) From equation (1) and (3), `2I_(1) = - 3I_(3) =- 4I_(3)` `therefore I_(1) = - 2I_(3) ""` .... (4) Applying KVL in the closed path ADCEFA , we get, `- 5I_(2) - 10 (I_(2) + I_(3)) - 10t = - 10` `therefore 15 I_(2) + 10I_(3) + 10I = 10` `therefore 15 I_(2) + 10 I_(3) + 10 (I_(1) + I_(2)) = 10 ` `therefore 10I_(1) + 25 I_(2) + 10 I_(3) = 10` `therefore 10 (-2I_(3)) + 25 (- 3I_(3)) + 10I_(3) = 10` `therefore - 85I_(3) = 10 ` `therefore I_(3) = - (10)/(85) = - (2)/(17) A ""` ... (5) From equation (4) and (5). From equation (4) and (5) , `I_(1) = - 2 (- (2)/(17))= (4)/(17) A ` ... (6) From equation (3) and (5) `I_(2)= - 3 (- (2)/(17))= (6)/(17) A "" `.... (7) now , `I = I_(1) + I_(2) = (4)/(17) + (6)/(17) = (10)/(17) A "" `....(8) From equation (5) , `| I_(3) | = (2)/(17)` A (Direction of `I_(3)` will be opposite to the direction shown in the figure ). Final answer : (i) Current in branch AB is, `I_(1) = (4)/(17) `A (ii) Current in branch BC is, `I_(1) - I_(3) = (4)/(17) - ( - (2)/(17)) = (6)/(17) A ` (iii) Current in branch CD is, `I_(2) + I_(3) = (6)/(17) + (- (2)/(17)) = (4)/(17)` A (iv) Current in branch DA is, `I_(2)= (6)/(17) `A (v) Current in branch BD is, `| I_(3)| = (2)/(17) A ` (Direction will be from D to B) (VI) Current in branch FE is, I = `(10)/(17) A ` |
|
| 42995. |
A generator produces a voltage that is given by V = 311 sin 314 t, where t is in seconds. The frequency and rms voltage are |
|
Answer» 314 Hz, 311 V |
|
| 42996. |
A ship is sailing due east according to Mariner's compass. If the declination of that place is 18^(@) east of north, what is the actual direction of the ship? |
| Answer» SOLUTION :`18^(@)` SOUTH to EAST | |
| 42997. |
List out the laws of photoelectric effect. |
|
Answer» Solution :Laws of PHOTOELECTRIC effect: • For a given frequency of incident light, the number of photoelectrons emitted is directly proportional to the intensity of the incident light. The saturation current is also directly proportional to the intensity of incident light. • Maximum KINETIC energy of the photo electrons is independent of intensity of the incident light. • Maximum kinetic energy of the photo electrons from a given metal is directly proportional to the frequency of incident light. • For a given surface, the emission of photoelectrons takes PLACE only if the frequency of incident light is greater than a certain MINIMUM frequency CALLED the threshold frequency. • There is no time lag between incidence of light and ejection of photoelectrons. |
|
| 42998. |
If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be(a)going up with increasing speed(b) going down with increasing speed(c ) going up with uniform speed(d) going down with uniform speed |
|
Answer» a, B are TRUE |
|
| 42999. |
The focal lengths of a lens are in the ratio 8:3 when it is immersed in two different liquids ofrefractive indices 1.6 and 1.2 respectively. The refractive index of the material of the lens is |
|
Answer» 1.25 |
|
| 43000. |
(a) When monochromatic light is incident on a surface separating two media, the reflected and refracted ligth both have the same frequency as the incident frequency. Explain why ? (b) When light travels from a rarer to a denser medium, it loses speed. Does the reduction in speed imply a reduction in energy carried by the light wave ? ( c) In the wave picture of light, intensity of ligth is determined by the square of amplitude of wave. What determines the intensity of light in teh photon picture of light ?(NCERT Solved Example) |
|
Answer» Solution :(a) The refelction and refraction of light occur on account of interaction of light with the atoms of the surface of SEPARATION. These atoms can be regarded as oscillators. Light incident on the interface forces the atomic oasillators to osillate with frequency of incident light. As frequency of light emitted by these (CHARGED) oscillators is equal to their own frequency of osillation, therefore, relfectedand refracted light have the same frequency as that of incident light. (b) No, energy carried by the wave does not DEPEND on its speed. Instead, it depends on the amplitude of wave. ( c) In the photon picture of light, the intensity of light at a point is determined by the NUMBER of photons per unit area AROUND the point. |
|