Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 37851. |
Two capillary tubes of lengths in the ratio 2:1 and radii in the ratio 1:2 are connected in series. Assume the flow of the liquid through the tube is steady. Then, the ratio of pressure difference across the tubes is |
|
Answer» `1:8` |
|
| 37852. |
The gravitational potential at centre of earth is |
|
Answer» `-(2GM)/R` |
|
| 37853. |
The units and dimensions of impedance in terms of charge Q are |
|
Answer» ohm, `ML^(2)T^(-2)Q^(-2)` |
|
| 37854. |
The dimensional formula for Torque is |
|
Answer» `M^(2)LT^(-2)` |
|
| 37855. |
A particle executes SHM on a straight line. At two positions, its velocities are u and v while accelerations are alpha and beta respectively [beta gt alpha gt 0]. The distance between these two positions is |
|
Answer» `(U^(2)+V^(2))/(ALPHA+ beta)` |
|
| 37856. |
Consider a long steel bar under a tensile stress due to force F acting at the edges along the length of the bar (as shown in figure). Consider a plane making an angle with the length. What are the tensile and shearing stresses on this plane? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ? |
Answer» Solution :THINK below figure, 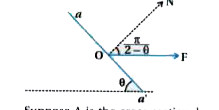 Suppose A is the cross sectional area of the bar. Let for balance of pane aa. angle `pi/2 - theta` between perpendicular ON to the pane and FORCE F. The parallel component of force to the pane, `F_(P) = F sin ((pi)/(2) - theta) = F cos theta and ` Perpendicular component, `F_(N) = F cos ((pi)/(2) -theta)= F sin theta` Suppose A is area of pane (face) aa. `therefore (A)/(A.) = sin theta` `therefore A. = (A)/(sin theta )` Tensile stress `= ("perpendicular force")/("area") = (F _(N))/(A.)= (F sin thea)/(A//sin theta)` `therefore` Tensile stress `= F/A sin ^(2) theta ` (a) For MAXIMUM stress `F/A sin ^(2) theta ` should be maximum. `sin ^(2) theta =1` `therefore sin theta =1` `therefore theta = (pi)/(2)` For this `theta = 90^(@)` Shearing stress `= ("parallel force")/("area") = (F _(p ))/(A.)` ` = (F cos theta )/(A //sin theta) = F/A sin theta cos theta= (F)/(2A) xx sin 2 theta` `[ because 2 sin theta cos theta = sin 2 theta]` (b) For shearing stress to be maximum `sin 2 theta =1` `therefore 2 theta =90^(@)` `therefore theta = 45^(@)` |
|
| 37857. |
If at STP, velocity of sound in a gas (y=1.5) is 600m//s, the rms velocity of the gas molecules at STP will be |
|
Answer» `400m//s` |
|
| 37858. |
A satellite appears to be at rest when seen from. the equator of the earth. The height of the satellite from the surface of the earth is |
|
Answer» 36000km |
|
| 37859. |
If an experiment to measure coefficient of viscosity radius of tube measured r = (0.100 +- 0.001) cm and length 1 = (50.0 +- 0.1) cm and volume of fluid coming out of capillary in unit time is V = (0.25 +-0.01) cm//^(2). If pressure difference between end of tube is p = 10^(6) dyne/ cm^(2), then by using Poeisullie's law V=(pi pr^(4))/(8 eta l) Find coefficient of viscosity. |
|
Answer» Solution :By using Poesullie.s law. `V=(pi p r^(4))/(8 etal)` `:. eta=(pi p r^(2))/(8 Vl) ""...(1)` `=(3.14xx10^(6)xx(0.1)^(4))/(8xx50xx0.25)` `=3.14` POISE Relative error in `eta` `(Delta eta)/(eta)=((Deltar)/(r))+((DeltaV)/(V))+((Deltal)/(L)) "" [ :. (pi)/(8)` CONSTANT ] `=4xx(0.001)/(0.1)+(0.01)/(0.25)+(0.1)/(50)` `=0.04+0.04+0.002` `=0.082` `:.(Delta eta)/(3.14)=0.082` `:.Delta eta=0.0082xx3.14` `=0.25748~~0.257` `:. eta+Deltan=(3.14+-0.257)` Poise OR Second method : `(Delta eta)/(eta)XX100%=0.082xx100%` `=8.2` `:. eta=3.14+-8.2%` Poise |
|
| 37860. |
A mass attached to a spring is free to oscillate, with angular velocity omega, in a horizontal plane without friction or damping. It is pulled to a distance x_(0) and pushed towards the centre with a velocity v_(0) at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters omega, x_(0) and v_(0). [Hint : Start with the equation x = a cos (omegat+theta) and note that the initial velocity is negative.] |
| Answer» SOLUTION :`sqrt((x_(0)^(2)+(v_(0)^(2))/(OMEGA^(2))))` | |
| 37861. |
For isothermal process of an ideal gas (dP)/P= _____ |
|
Answer» SOLUTION :`-(DV)/V` For isothermal PROCESS PV=constant, Differentiate it `THEREFORE` PdV+dPV=0 `therefore` dPV=-PdV `therefore (dP)/P=-(dV)/V` |
|
| 37862. |
What is the physical quantity of the time rate of the angular momentum? |
| Answer» SOLUTION :The time rate of change of angular MOMENT indicates TORQUE `(dvecL)/(DT)=vectau` | |
| 37863. |
which of the following is a unitless quantity |
|
Answer» velocity gradient |
|
| 37864. |
A student sees a jet plane flying from east to west. When the jet is seen just above his head, the sound of jet appears to reach him making angle of 60^(@) with the horizontal from the east. If the velocity of the sound is V, then that of the jet plane is |
|
Answer» `2V` |
|
| 37865. |
What do you mean by inertia of direction? Give one example. |
| Answer» SOLUTION :WHENA stonetiedto a STRINGIS in whiring motionand if thestringis cutsuddenlythe stonewill not continueto movein circularmotionbutmovestangentialto THECIRCLE. | |
| 37866. |
A small spherical ball is suspended through a string of length l. The whole arrangement is placed in a vehicle, which is moving with velocity v. Now suddenly the vehicle stops and ball stats moving along a circular path. If tension in the string at the highest point is twice the weight of the ball, then |
|
Answer» `v=SQRT(5gl)` |
|
| 37867. |
At what points is the energy entirely Potential in SHM ? |
| Answer» SOLUTION :ENERGY is POTENTIAL at EXTREME POSITION. | |
| 37868. |
If the length of the simple pendulum is equal to the radius of the earth, and it oscillates just above the surface of the earth then its time period is a) 2pisqrt((R)/(2g))(b)2pisqrt((R)/(g)) c) nearly 59.5 minutes d) 84.6 minutes |
|
Answer» a is only CORRECT |
|
| 37869. |
Two identical billiard balls strike a rigid wall with the same speed but at different angles, and get reflected without any change in speed,as shown in Fig. 5.6. What is (i) the direction of the force on the wall due to each ball? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ? |
|
Answer» Solution : An instinctive answer to (i) might be that the force on the WALL in case (a) is normal to the wall, while that in case (b) is inclined at 30° to the normal. This answer is wrong.The force on the wall is normal to the wall in both cases. How to find the force on the wall? The trick is to consider the force (or impulse) onthe ball due tothe wall using the second law, and then use the third law to answer (i). Let u be the speed of each ball before and after collision with the wall, and m the mass of each ball. CHOOSE the x and y AXES as shown in the figure, and consider the change in momentum of the ball in each case : Case (a) `(p_x)_("initial")` = mu`(p_y)_("initial") = 0` `(p_x)_("final")`= -mu`(p_y)_("final") = 0` Impulse is the change in momentum vector. Therefore , x-component of impulse=– 2 m u y-component of impulse=0 Impulse and force are in the same direction. Clearly, from above, the force on the ball due to the wall is normal to the wall, along the NEGATIVE x-direction.Using Newton’s third law of motion, the force on the wall due to the ball is normal to the wall along the positive x-direction. The magnitude of force cannot be ascertained since the small time taken for the collision has not been specified in the problem. case (b) `(p_x)_("initial") = ` mu cos `30^@ , (p_y)_("initial") = ` - mu sin `30^@` `(p_x)_("final")`= - mu cos `30^@ , (p_y)_("final") = ` - mu sin `30^@` NOTE while `p_x` changes sign after collision , `p_y` does not. therefore x - component of impulse= - mu `cos 30^@` y = component impulse = 0 The direction of impulse (and force) is the same as in (a) and is normal to the wall along the negative x direction.As before, using Newton’s third law, the force on the wall due to the ball is normal to the wall along the positive x direction. The ratio of the magnitudesof the impulses imparted to the balls in (a) and (b) is 2mu/(2mu cos `30^@`) = `(2)/(sqrt3) = 1.2` |
|
| 37870. |
Two moles of a perfect gas heated to increaseits temperature by 4^(@)C absorbs heat of 32 Cal at constant volume. If the same gas is heated at constant pressure the amount of heat supplied is (R = 2 Cal /mol K) |
| Answer» Answer :B | |
| 37871. |
The smallest physical unit of time is………….. |
|
Answer» second |
|
| 37872. |
Which of the following qauntities is dependent of the choice of orientation of coordinates axes? |
|
Answer» `vecA + vecB` but the QUANTITY `A_(x) + B_(y)` depends upon the magnitude of the COMPONENT along x and y-axes, SOIT will change with change in coordinate axes. |
|
| 37873. |
Which of the following is not characteristics of simple harmonic motion? |
|
Answer» The motion is periodic |
|
| 37875. |
can a heat engine convert full intake of heat into work ? |
| Answer» Solution :no according to second law of THERMODYNAMICS the whole of HEAT cannot be CONVERTED into work | |
| 37876. |
A bicycle is motion. The force of friction exerted by the ground on its wheel is such that it acts : |
|
Answer» in FORWARD direction on both wheel it is ACCELERATING |
|
| 37877. |
A body of mass m is moved to a height to equal to the radius of earth.The increase in P.E is |
|
Answer» mgR |
|
| 37878. |
The difference in the value of .g. at pole and at a latitude is (3)/(4)Rw^(2) then latitude angle is |
|
Answer» `60^(@)` |
|
| 37879. |
A body executing forced oscillations under driving force is in sharp resonance. If damping increases, then sharpness of resonance |
|
Answer» DECREASES |
|
| 37880. |
A: During takeoff of an aeroplane, velocity of air above the wing is greaterthan velocity below the wing R: Bernoulli.s principle is based on law of conservation of energy |
|
Answer» Both A and R are TRUE and R is the CORRECT explanation of A |
|
| 37881. |
In damped oscilation the directions of the restoring force and the resistive force |
|
Answer» are the same |
|
| 37882. |
A body with constant acceleration always moves along a straight line. A body with constant magnitude of acceleration may not speed up. |
|
Answer» Statement (I) is true, Statement (II) is true , statement (II) is the CORRECT EXPLANATION for Statement (I). A body with constant magnitude of acceleration may not speed up, this is POSSIBLE in UNIFORM circular motion. |
|
| 37883. |
The frequency of vibrating air column in closed organ pipe is n. If it length be boubled and radius halved. Its frequency will be nearly : |
|
Answer» `(n)/(2)` `n=(v)/(4L) rArr n PROP (1)/(L)` If `L=2L` Then `n' prop (1)/(2L)` `(n')/(n')=(L)/(2L)` (or) `n'(n)/(2)` Radius has no effect on frequency. |
|
| 37884. |
The maximum distance to which a man can throw a ball by projecting it horizontally from a height h is h. The maximum distance to which he can throw it vertically up is |
|
Answer» h |
|
| 37885. |
Heat is associated with |
|
Answer» kinetic ENERGY of RANDOM MOTION of molecules. |
|
| 37886. |
What is the effect of decreasing the height of a satellite orbiting around earth on its time period? |
| Answer» SOLUTION :`IMPLIES` Time period of satellite `T=2pisqrt(((R_e+h)^3)/(GM_e))`hence, h decreases, its time period decreases. | |
| 37887. |
A block is dragged on a smooth plane with the help of a rope which moves with velocity (v) shown in Fig. 2 (CF). 25 , The horizontal velocity of the block is . |
|
Answer» `v` :. ` (d(AC)/(dt) = d/(dt) (x cos theta) = (DX)/(dt) cos theta + x (- sin theta) (d theta)/(dt)` But `(d(AC)/(dt) = 0 `, so ` 0= (dx)/(dt) cos theta + x ( - sin theta) ( d theat)/(dt)` or ` v cos theta = x sin theta = x sin theta (d theta)/(dt)` or ` (dtheta)/(dt) = ( v cos theta)/(x sin theta)` 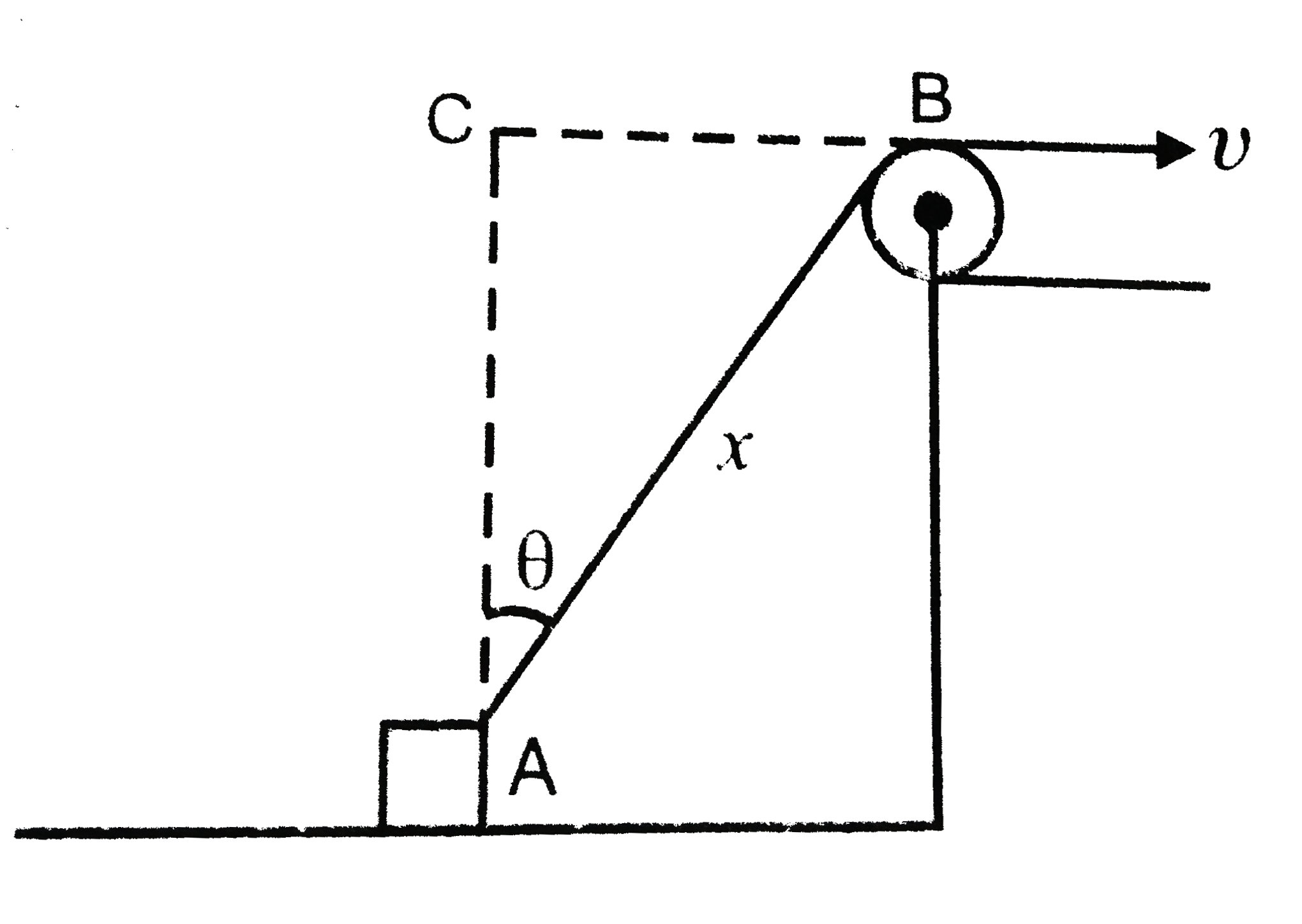 . . Also , ` CB = x sin theta`. Velocity of block will be ` u = sin theta + x cos theta xx (v cos theta)/( x sin theta)` ` (v (sin^@ theta + cos^2 theta)/( sin theta) = v/(sin theta)`. |
|
| 37888. |
The magnitude of gravitational potential energy of the moon-earth system is U with zero potential energy at infinite separation. The kinetic energy of the moon with respect to the earth is K. |
| Answer» Answer :B | |
| 37889. |
Which of the following potential energy curves in figure cannot describe the elastic collision of twobilliard balls ? Here r is the distance between centres of the balls . |
|
Answer» Solution :Distance between centre of BALLS is 2R when both ball collide . During every elastic collision , the shape of ball slightly CHANGES . In elastic collision potential energy CONVERTED into kinetic energy . The potential energy of a system of two masses is inversely proportional to the separation between them . ` :.V prop 1/r` Out of the given graph , curve (v) only satisfies these two CONSITIONS .Therefore , all other curves cannot possibly describe the elastic collision of two billiard balls . |
|
| 37890. |
Prove that the ratio of the rate of change of g at a height equal to the earth's radius from the surface of the earth of the value of g at the surface of the earth is equal to (-1)/(4R_e) |
|
Answer» Solution :`implies` Gravitational acceleration at .r. `(r GE R_e)`from the CENTRE of EARTH . `g(r) = (GM_e)/r^2` Differentiating w.r.t. to DISTANCE r, `(dg(r))/(DR) = (-2GM_e)/r^3` `= -(2GM_e)/((8R_e)R_(e)^2)[ :. (GM_e)/R_e^2="ge"]` `:. [(dg(r))/(dr)]_(2R_e) =(-"ge")/(4R_e)` =`[(dg(r))/(dr)]_(2Re)/("ge")=-1/(4R_e)` . |
|
| 37891. |
For a gas at a temperature T the Root mean square velocity v_(rms) ,the most probable speed v_(mp),and the average speed a_(av) obey the relationship |
|
Answer» `v_(AV) gt v_(RMS) gt v_(mp)` |
|
| 37892. |
Three particles A, B and C of respective masses m_(1), m_(2) and m_(3) lie on a smooth horizontal surface, and an fastened to two light inextensible strings as shown in Fig. The particle A is imparted an impulse J along vec(BA) . Find the initial speed of each particle. |
|
Answer» SOLUTION :`J-J_(1)=m_(1)v_(1)` ………i `J_(1)-J_(2)(cos45^(@))=m_(2)v_(2y)`…………..ii  `J_(2)sin45^(@)=m_(2)v_(2x)`…………..iii `J_(2)=m_(3)v_(3)` ……………iv. Now `v_(2y)=v_(1)` and `v_(2y)cos45^(@)-2_(2x)cos45^(@)=v_(3)` Solve to get `v_(y)=(sqrt2m_(2)J)/(m_(1)m_(3)+2m_(2)(m_(1)+m_(2)+m_(3)))` `v_(1)=((m_(3)+2m_(2))J)/(m_(1)m_(3)+2m_(2)(m_(1)m_(2)+m_(3)))` `v_(2x)=(m_(3)v_(3)cos45^(@))/m_(2)=(m_(3)J)/(m_(1)m_(3)+2m_(2)(m_(1)+m_(2)+m_(3)))` Net velocity of `m_(2)` `=sqrt(v_(1)^(2)+v_(2x)^(2))=(sqrt2(m_(2)^(2)+(m_(2)+m_(3))^(2))^(1//2))/(m_(1)m_(3)+2m_(2)(m_(1)+m_(2)+m_(3)))` |
|
| 37893. |
The value of resistance is 10.84 ohm and current is 3.23 A . The potential difference is 35.02935 V its value in significant number will be |
|
Answer» 35 V |
|
| 37894. |
The length of a metallic sheet is measured as 10.0 cm using a metre scale of L.C. 0.1cm and its breadth is measured as 1.00 cm using a vernier callipers of L.C. 0.01cm, the error in area is |
|
Answer» `pm0.01 cm^2` |
|
| 37895. |
Give any two examples for parallelogram law of vectors. |
| Answer» Solution :(i) the FLIGHT of a BIRD (II) WORKING of a sling. | |
| 37896. |
The minimum force required to move a body up an inclined plane is three times the minimum force required to prevent it from sliding down the plane. If the coefficient of friction between the body and the inclined plane (1)/(2sqrt3),is the angle of the inclined plane is |
|
Answer» `60^(@)` |
|
| 37897. |
In which process, the p - v indicator diagram is a straight line parallel to volume axis? |
|
Answer» ISOTHERMAL |
|
| 37898. |
A nucleus is at rest in the laboratory frame of reference.Show that if it disintegrates into two smaller nuclei the products must move in opposite directions. |
| Answer» Solution : By MOMENTUM conservation PRINCIPLE, TOTAL final momentum is zero.Two momentum vectors cannot sum to a NULL momentum unless they are equal and opposite. | |
| 37899. |
An aircraft is flying at a height of 3400mabove the ground . If the angle subtended at a ground observation point by the aircreaft positions 10.0 s apart is 30^(@) , what is the speed of the aircraft ? |
Answer» Solution :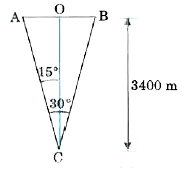 LET A and B be the positions of the aircraft for which ` ANGLE ACB=30^(@)` Time TAKEN by the aircraft to go from A to B =10 s Here OC =3400 m `tan 15^(@)=(OA)/(OC)` `RARR OA=OC tan 15^(@)` `=3400xx0.267=907.8m` Speed of aircraft` =("Distance "AB)/("Time")` `=(2xxOA)/(10 s)=(2xx907.8)/(10)` `=181.56`m |
|
| 37900. |
Assertion : Rule is an example for Orthogonal vectors. Reason : When we stretch first three fingers of our right hand, Magnetic field along fore finger (i.e. X- axis ) current direction along middle finger (i.e. Y - axis ) and motion of the conductor along the thumb direction (i.e. Z axis) |
|
Answer» Assertion and Reason are CORRECT and Reason is correct explanation of Assertion |
|