Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 44801. |
On any planet, the pressure of atmosphere implies (C_(rms) = root mean square velocity of molecules and v_(e) = escape velocity) |
|
Answer» `C_(rms)ltltv_(e)` |
|
| 44802. |
Unit of ………………..is Wb m^(-2) and it may also be written as ………………… . |
| Answer» Solution :magnetic FIELD (or magnetic FLUX density), TESLA | |
| 44803. |
The current in an inductive circuit is given by 0.3 sin(200t - 40^(@)) A. Write the equation for the voltage across it if the inductance is 40 mH. |
|
Answer» SOLUTION : `L = 40 xx10^(-3H), i = 0.1 sin (200t-40^(@)), X_(L) = omegaL= 200 x× 40 x× 10^(-3) = 8Omega, V_(m)=I_(m)X_(L)= 0.3 xx 8 = 2.4 V` In an INDUCTIVE circuit, the voltage leads the current by `90^(@)` THEREFORE, `upsilon = V_(m) sin (omega +90^(@))` `upsilon = 2.4 sin (200t - 40^(@)+90^(@))` `upsilon = 2.4 sin (200t +50^(@))vol t` |
|
| 44804. |
Relativistc formula for kinetic energy is "______________" |
|
Answer» `E_(k) = mc^(2)` |
|
| 44805. |
The internationally accepted frequency deviation for the purpose of FM broadcasts. |
| Answer» Answer :a | |
| 44806. |
Explain briefly, with the help of circuit diagram , how V-I characteristics of a p-n junction diode are obtained in (i) forward bias, and (ii) reverse bias. Draw the shapes of the characteristic curves obtained. Or Explain briefly, with the help of necessary diagrams, the forward and the reverse biasing of a p-n junction diode. Also draw their characteristic curves in the two cases. |
|
Answer» Solution :WORKING of a p-n JUNCTION diode can be studied in (i) FORWARD bias, and (ii) reverse bias arrangement. To study characteristics of a p-n junction in these biasing arrangement we proceed as follows (i) Forward bias : In forward bias arrangementp-side of p-n junction is connected to +ve terminal of battery and n-side to -ve terminal of battery as shown in . A voltmeter V and a milliammeter mA are joined as shown in figure. The voltage applied to p-n junction can be altered by using a rheostat with battery. In forward bias, the current `I_(e)` first increases very slowly till a certain threshold voltag ( ~ 0.7 V for silicon diode) is reached. After the threshold voltage, the diode current increases exponentially even for a very small increase in the diode bias voltage. The characteristic curve is shown in. (ii) Reverse bias: In reverse bias arrangementp-side of p-n junction is connected to -ve terminal and n-side to +ve terminal of battery as shown in . A voltmeter V and a microammeter uA (since current in reverse bias is extremely small) are also connected as shown. In reverse bias the battery is capable of providing a voltage of even up to 100 V. Inreverse bias, the current `I_(R)` is very small and ALMOST remains constant with change in reverse bias voltage `V_(R)`. It is called "reverse saturation current". However, at very high reverse bias the current suddenly increases. This voltage is known as the breakdown voltage or zener voltage. The characteristic curve is shown in .  
|
|
| 44807. |
Four point charges q_(A) =2 muC, q_(B) = -5 muC, q_(C) =2 muC, and q_(D) = -5 muCare located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1 muCplaced at the centre of the square ? |
Answer» Solution :Situation GIVEN in the statement is depicted ii the FOLLOWING figure. 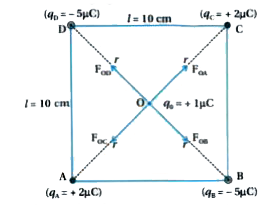 Magnitude of Coulombian force exerted of `q_(0)` by `q_(A)` is, `F_(OA) = K(q_(0)q_(A))/R^(2)` (From A to O) …………..(1) Magnitude of Coulombian force exerted on `q_(0)` by `q_(C)`, is `F_(OC) =k(q_(0)q_(C))/r^(2) = k(q_(0)q_(A))/r^(2) (THEREFORE q_(C) = q_(A))` From C to O ..........(2) From eqn (1) and (2) `vecF_(OA) = -vecF_(OC)`...........(3) Magnitude of Coulombian force exerted on `q_(0)` by `q_(B)` is `F_(OB) = k(q_(0)q_(B))/r^(2)` (From O to B)...........(4) `F_(OB) = -F_(OB)`..........(6) Now, resultant Coulombian force exerted on `q_0` by remaining charges is, `vecF_(O) = vecF_(OA) + vecF_(OB) + vecF_(OC) + vecF_(OD) = vecO` `therefore F_(O) =0` |
|
| 44808. |
Refractive index of red and violet light are 1.52 and 1.54 respectively. If the angle of prism in 10^(@). The angular dispersion will be |
|
Answer» `0.02^(@)` |
|
| 44809. |
An ammeter reads 2mA at full scale deflection and has an internal resistance of 100Omega.if it is to be converted in to voltmeter to read 20 V at full scale the value of resistance required is : |
|
Answer» `99900Omega` |
|
| 44810. |
The heat capacity per mole of water is (R is universal gas constant) : |
|
Answer» 9R `U=3xx3k_(B)TxxN_(A)=9RT(becausek_(B)=R/(N_(A)))` `therefore` Heat capacity PER mole of water is `C=(DeltaQ)/(DeltaT)=(DeltaU)/(DeltaT)=9R` Correct CHOICE is (a). |
|
| 44811. |
A radioactive nucleus can decay simultaneously by two different processes which have decay constants lambda_1 and lambda_2. The effective decay constant of the nuclide is lambda, where : |
|
Answer» `LAMBDA = lambda_1 + lambda_2` |
|
| 44812. |
Experiments show the electrical conductivity of semiconductors to rise drastically with temperature. Assuming that it is possible to calculate the probability of electron transition from the valence to the conduction band using the barometric distribution, derive the formula for the temperature dependence of a semiconductor's conductivity. |
|
Answer» `GAMMA=(e^(2)lamdaA)/(pF)e^(-Deltaepsi//kT)=Re^(-Deltaepsi//kT)` where B is a constant characteristic of the material (at a SPECIFIED temperature). |
|
| 44813. |
A charge q is revolving in a circular path of radius r with a constant speed v. Its magnetic moment is given as |vec| = ……………… . |
| Answer» SOLUTION :`1/2 QVR` | |
| 44814. |
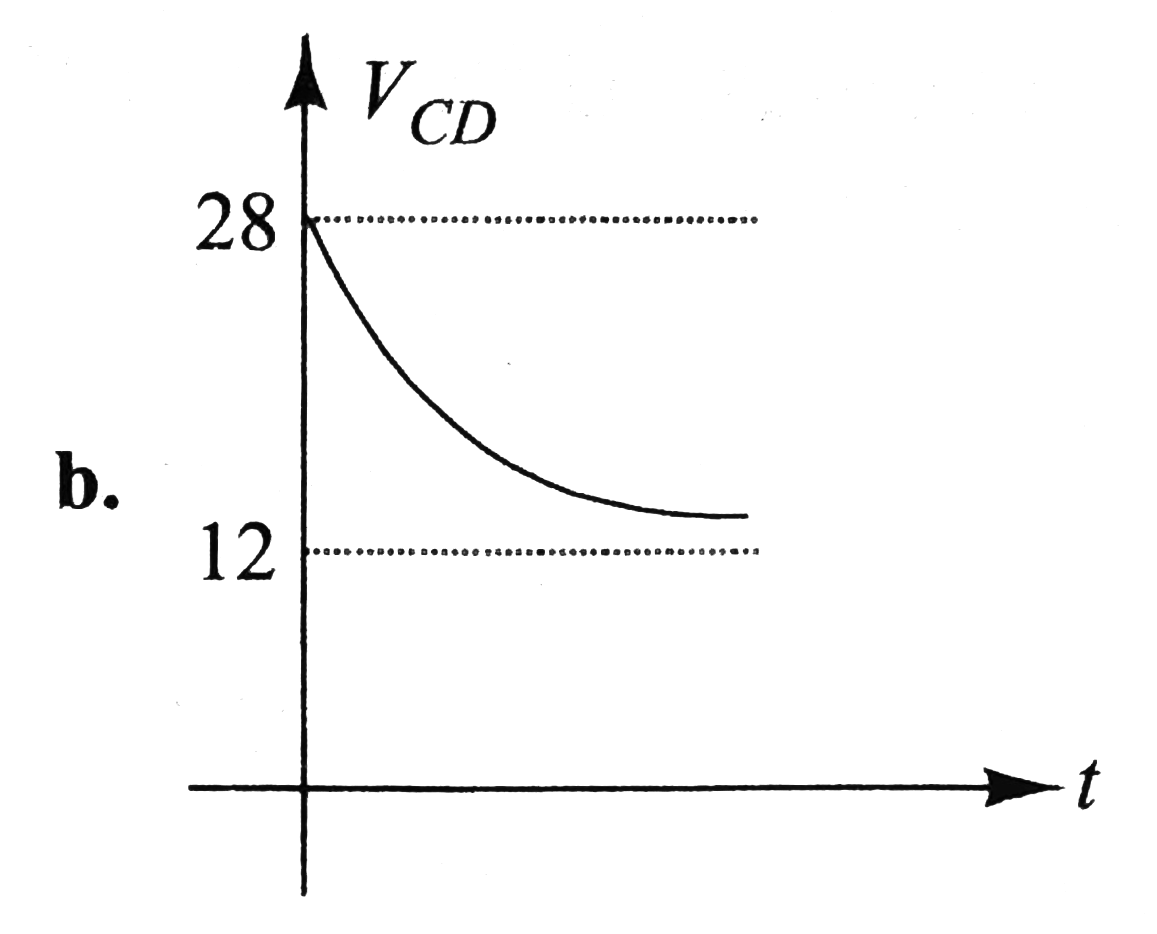
In Fig i_(1) = 10e^(-2t) A, i_(2) = 4 A, and V_(C) = 3e^(-2t) V. The variation of potential difference across C and D(V_(CD)) with time can be expressed as |
|
Answer»
`q = CV_(C) = (2)(3e^(-2t)) = 6e^(-2t) A` Current, `i_(C) = (dq)/(dt) = - 12e^(-2t)A` This current flows from `B` to `O`. From `KVL`, we have `i_(L) = i_(1) + i_(2) + i_(C) = 10e^(-2t) + 4 - 12e^(-2t)` `= (4 - 2t^(-2t)) A = [2 + 2(1 - E^(-2t))]A` `i_(L) vs`. time graph is as shows in Fig lt `i_(L)` increases from `2 A` to `4 A` expontially.  `V_(L) = L(di_(L))/(dt)` `= (4)(d)/(dt) (4 - 2e^(-2t)) = 16e^(-2t) V` `V_(L)` decreases exponentially from `16 A` to `0` as shows in Fig. To determine `V_(AC)`, we begin from `A` and at `C`. From `KVL`, we have  `V_(A) - i_(1)R_(1) + i_(2)R_(2) = V_(C)` `V_(A) - V_(C) = i_(1)R_(1) - i_(2)R_(2)` Substituting the values, we have `V_(AC) = (10 e^(-2t))(2) - (4)(3)` 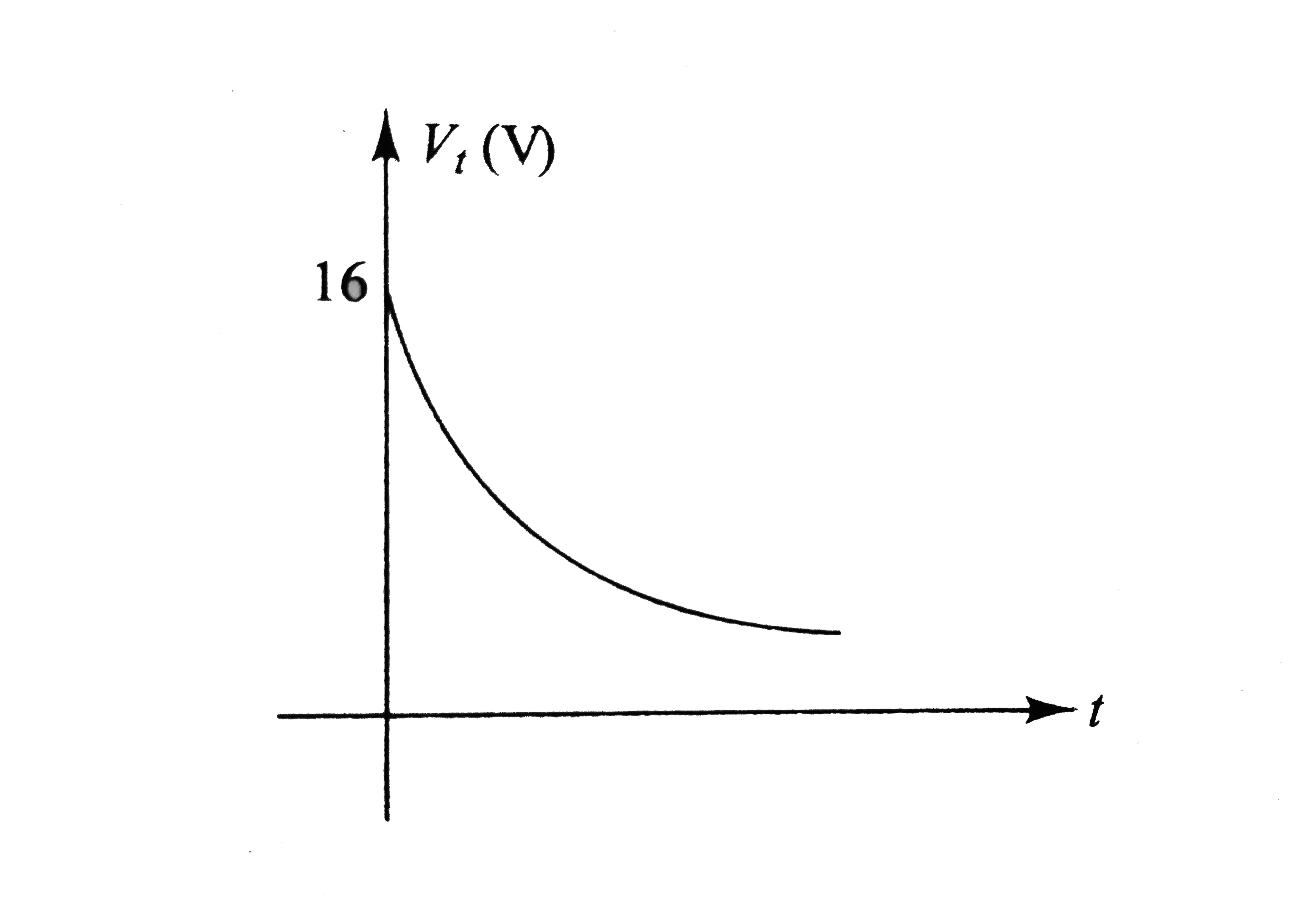 `V_(AC) = (20e^(-2t) - 12) V` At `t = 0`, `V_(AC) = 8V` At `t = oo`, `V_(AC) = - 12 V` Therefore, `V_(AC)` decrease exponentially from `8 V` to `12 V`. Similarly, we have from `A` to `B` `V_(A) - i_(1)R_(1) + V_(C) = V_(B)` `V_(AB) = V_(A) - V_(B) = i_(1)R_(1) - V_(C)` 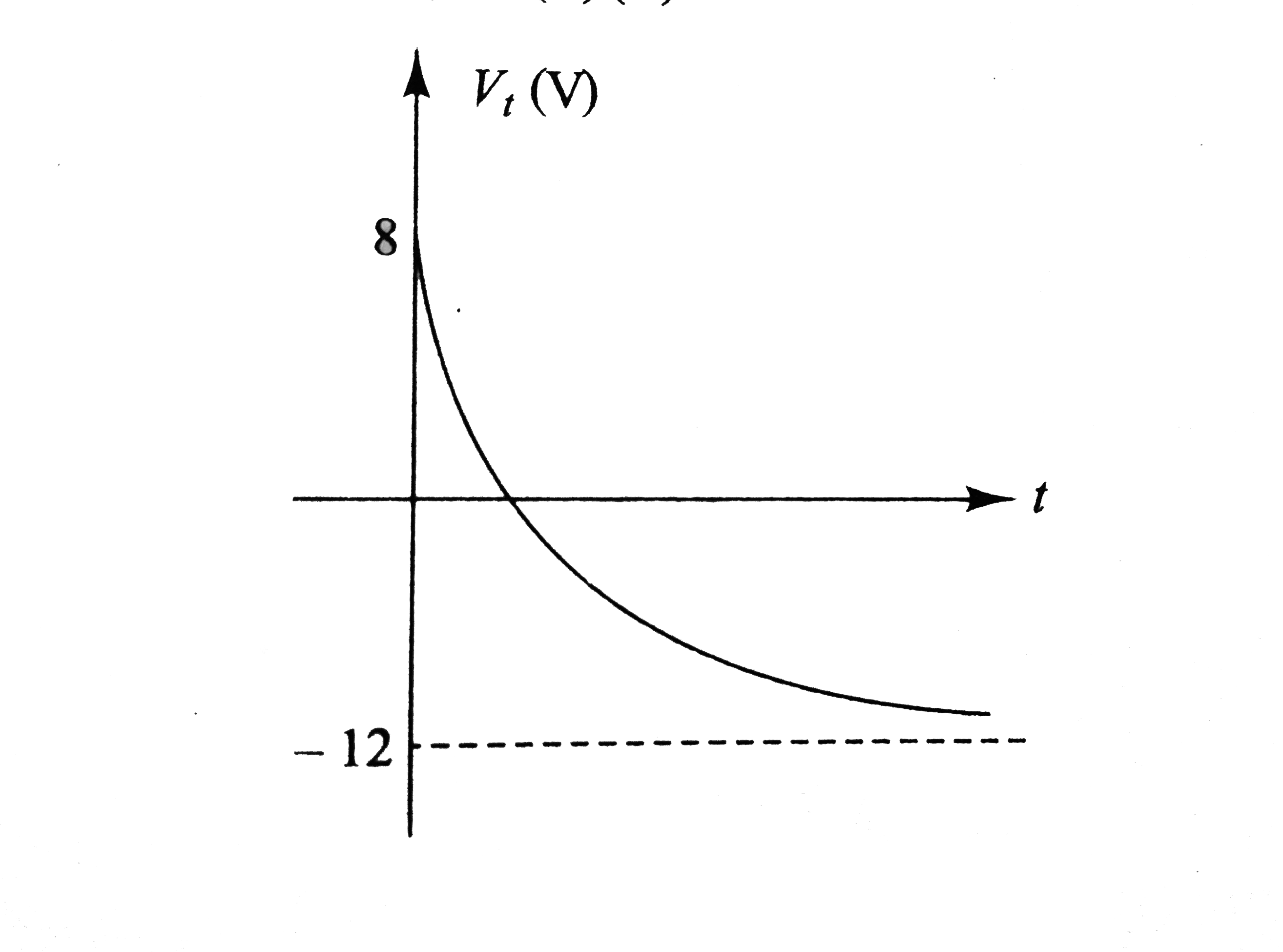 Substituting the values, we have `V_(AB)=^((10e^(-2t)))(2)-3e^(-2t)` `V_(AB) =^(17e^(-2t))V` Thus, `V_(AB)` decreases exponentially from `17 V` to `0`. As we move from `C` to `D`, `V_(C) - i_(2)R_(2) - V_(L) = V_(D)` `V_(CD)= V_(C) - V_(D) = i_(2)R_(2) + V_(L)` Substituting the values we have, `V_(CD)= (4)(3) + 16e^(-2t)` 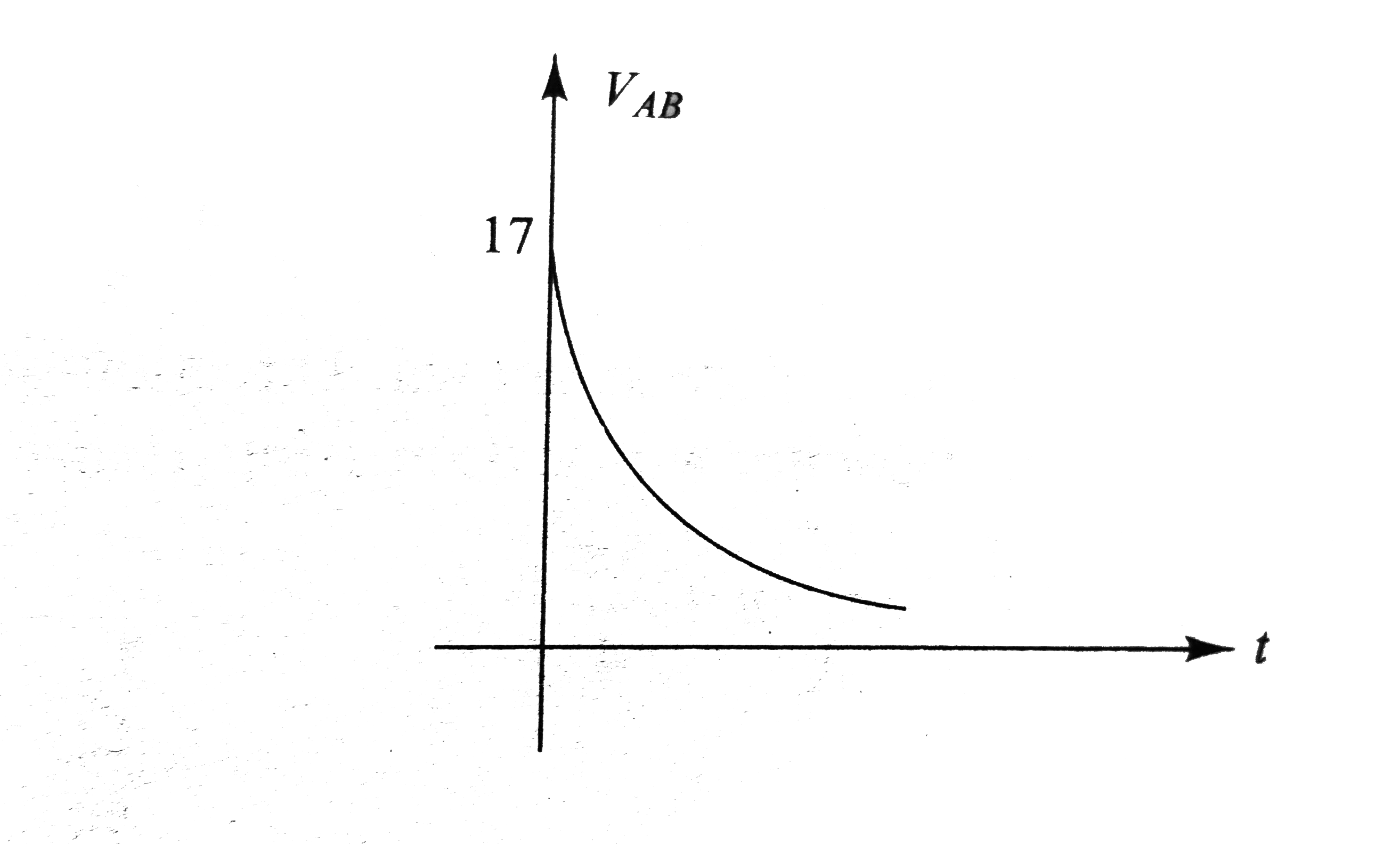 `V_(AD) = (12 + 16e^(-2t))V` At `t = 0, V_(CD) = 28 V` and at `t = oo, V_(CD) = 12 V` i.e., `V_(CD)` decreases exponentially from `28 V` to `12 V`. |
|
| 44815. |
Pick out the incorrect statement from the following . |
|
Answer» `beta^-` emission from the nucleus is always accompanied with a neutrino The `beta^-` DECAY is `n to p + underset"electron"(e^(-)) + underset"antineutrino"(barv)` |
|
| 44816. |
Two blocks of mass M and 3M (in kg) are connected by an inextensible light thread which passes over a light frictionless pulley. The whole system is placed over a fixed horizontal table as shown.The coefficient of friction between the blocks and table surface is mu. The pulley is pulled by a string sttached to its centre and accelerated to left with acceleration a((m)/(s^2)). Assume that gravity acts with constant acceleration g((m)/(s^2)) downwards through the plane of table. Then: (a) Find the forizontal accelration of both the blocks (Assume that both the blocks are moving.) (b) What is the maximum acceleration a, for which the block of mass 3 M will remain stationary? |
Answer» Solution :  (a) Let the ACCELERATION of blocks of mass M and 3 M are `a_1` and `a_2` RESPECTIVELY. From constraint RELATION `a_(pulley)=(a_1+a_2)/(2)=a`.(i) F.B.D. of BLOCK of mass M `T-muMg=Ma_1`.(ii) F.B.D. of block of mass 3 M `T=(-3mu)/(MG)=3Ma_2` .(iii) From (ii) and (iii): `-muMg=3muMg=Ma_1-3Ma_2` `implies2mug=a_1-3a_2` From (i) and (iv) `2mug=(2a-a_2)-3a_a` `impliesa_2=(a-mug)/(2)` From (i) and (v) `a_1=2a-a_2=2a-((a-mug)/(2))=(3a)/(2)+(mug)/(2)=(3a+mug)/(2)` (b) Since `a=(a_1+a_2)/(2)` Acceleration a will be maximum when `a_1` is maximum (since`a_2=0`) Acceleration `a_1` is maximum when tension in the string is maximum for block of mass 3 M to be stationary `Tle3muMg` `T_(max)=3muMg` For block of mass M `T_(max)-muMg=Ma_1` `implies3muMg-muMg=Ma_1` `implies2mug=a_1` So maximum acceleration `a=(a_1+a_2)/(2)=(2mug+0)/(2)=mug` |
|
| 44817. |
In a biprism experiment, 62 fringes were observed with sodium light of wavelength 5893 A.U. Keeping the same arrangement, if sodium light is replaced by mercury light using green filter of wavelength 5461 A.U. how many fringes will be then observed ? |
|
Answer» 60 |
|
| 44818. |
A light wave has a frequency of 4xx10^(14)Hz and wavelength on a water [n_(w)=(4)/(3)] interface. The critical angle of incidence is ___________. |
|
Answer» Solution :Here `v=4xx10^(14)Hz and lambda=500 nm =5xx10^(-7)m` `RARR""v=upskon lambda=4xx10^(14)xx5xx10^(-7)=2xx10^(8)MS^(-1)` `rArr""N=(c)/(v)=(3xx10^(8))/(2xx10^(8))=1.5` |
|
| 44819. |
A straight conductor of length 4 metre moves at a speed of 10 m/s when the conductor makes an angle of 30^(@) with the direction of magnetic field of induction 0.1 weber per "metre"^(2). Then the induced e.m.f is |
|
Answer» Solution :INDUCED e.m.f. `e=Bvl sin theta =0.1xx10xx4 sin 30^(@)` `rArr e=2` volt |
|
| 44820. |
Three vectors vec A, vec B and vec C satisfy the relation vec A. vec B = O , vec A. vec C = O. If vec B and vec C are not lying in the same plane, then vec Ais parallel to |
|
Answer» `VEC B` |
|
| 44821. |
Monochromatic light of frequency 6.0 xx 10^(14) Hz is produced by a laser.The power emitted is 2 xx 10^(-3) w. The number of photons emitted, on the average, by the sources per second is |
|
Answer» |
|
| 44822. |
For more information about thin spherical lens, define : (a) First principal focus (F_1)(b) Second principal focus (F_2)(c) Optical centre (C) (d) Focal length (f) |
|
Answer» Solution :If a point object is placed on the principal axis of a convex lens such that the rays refracted are PARALLEL to the axis FIGURE (a), then the position of the point object is CALLED the first principal focus `(F_1)` of the lens, If the object is situated at infinite (figures (b) and (c)), refracted rays meet (or appear to meet) for convex (or concave) lens to a point `(F_2)`, then the position of this point is known as second principal focus `(F_2)`. The geometrical centre of the medium of the lens is called its OPTICAL centre (C). Distance of principal focus from the optical centre (C) is known as focal LENGTH (f) of the lens. As per the sign convention, f is positive for convex lens and negative for concave lens. |
|
| 44823. |
The amount of heat energy required to freeze 4.5 g ofwater of 6^(@)C to ice at 0^(@)C is [S=41900 J kg^(-1)K^(-1), L=3.33xx10^(5)Jkg^(-1)] |
|
Answer» 1612 J |
|
| 44824. |
(a) What happens if a bar magnet is cut into two pieces: (i) transverse to its length, (ii) along its length? (b) A magnetised needle in a uniform magnetic field experiences a torque but no net force. An iron nail near a bar magnet, however, experiences a force of attraction in addition to a torque. Why? (c) Must every magnetic configuration have a north pole and a south pole? What about the field due to a toroid? (d) Two identical looking iron bars A and B are given, one of which is definitely known to be magnetised. (We do not know which one.) How would one ascertain whether or not both are magnetised? If only one is magnetised, how does one ascertain which one? [Use nothing else but the bars A and B.) |
|
Answer» Solution :(a) In either case, one gets two magnets, each with a north and south pole. (b) No force if the field is uniform. The iron nail EXPERIENCES a non-uniform field DUE to the bar magnet. There is induced magnetic moment in the nail, therefore, it experiences both forcy and torque. The net force is attractive because the induced south pole (say) in the nail is closer to the north pole of magnet than induced north pole. (c) Not necessarily. True only if the source of the field has a net non-zero magnetic moment. This is not so for a toroid or een for a STRAIGHT infinite conductor. (d) Try to bring different ends of the bars closer. A repulsive force in some situation establishes that both are magnetised. If it is always attractive, them one of them is not magnetised. In a bar magnetic the intensity of the magnetic field is the strongest at the two ends (poles) and weakest at the central region. This fact may be used to determine whether A or B is the magnet. In this case, to see which one of the two bars is a magnet, pick up one, (say A) and lower one of its ends, first on one of the ends of the other (say B), and then on the MIDDLE of B. If you notice that in the middle of B, A EXPERIENCE no force, then B is magnetised. If you do not notice any change from the end to the middle of B, then A is magnetised. |
|
| 44825. |
In accordance with the Bohr’s model, find the quantum number that characterises the earth’s revolution around the sun in an orbit of radius 1.5 xx 10^(11) m with orbital speed 3 xx 10^4 m//s. (Mass of earth = 6.0 xx 10^(24) kg.) |
| Answer» SOLUTION :`2.6 XX 10^(74)` | |
| 44826. |
In the given figure, the faces of prism ABCD made of glass with a refractive index n form dihedral angles /_A=90^(@),/_B75^(@),,/_C=135^(@) & /_D=60^(@) (The Abbe's prism) .A beam of light falls on face AB & after total internal reflection from face BC escapes through face AD.Find the range of n and angle of incidence alpha of the beam onto face AB, if a beam that has passed through the prism in this mahner is perpedicular to the incident beam. |
|
Answer» `rArr` incidence angle at face `QD` is `r.` In quadrlateral `PQDC 15^(@)+r+135^(@)+r+90=180^(@)` Now, `75^(@)-r=45^(@)gtcrArr(1)/(sqrt2)gt(10/(N)rArrngtsqrt2` Also, `sin alpha =n sin r =n sin 30^(@)=(n)/(2)` `rArr n=2sin alpha rArr (n)/(2)le1rArrnle2` `therefore sqrt2lenle2` and `(sin alpha)/(sin r)=n rArrsqrt2 le'2sin alphale2` `rArr (1)sqrt2)ltsin alpha le1 rArr45^(@)ltalphale90^(@)`. 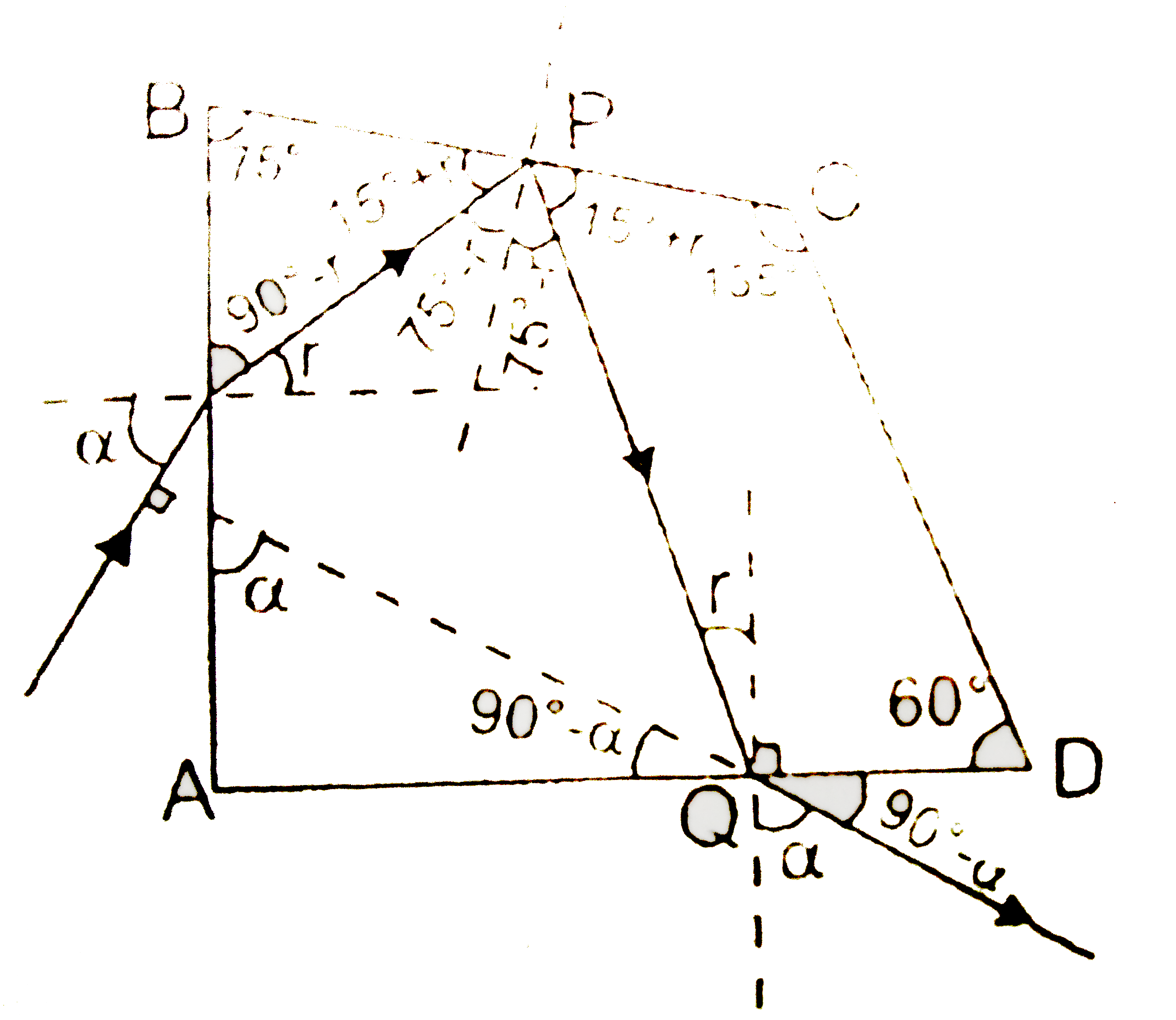
|
|
| 44827. |
Where wave theory had a failure ? |
| Answer» SOLUTION :PHOTOELECTRIC EFFECT. | |
| 44828. |
A person is riding a motorcycle at a speed v towards a stationary car operating its siren at Hz. A police car is chasing the person at a speed 22 m/s with its siren operating at 176 Hz. If the motorcyclist does not heard beats, the speed v (m/s) is (speed of sound in air = 330 m/s) |
|
Answer» 33 |
|
| 44829. |
A an electron is placed at the centre of the copper ring of problem 37. Show that if the electron is displaced a little, it will perform simple harmonic motion with a frequency f=1/(2Pi)sqrt((eq)/(4piepsilon_0ma^3)) |
| Answer» | |
| 44830. |
To draw thermo electric diagrams Lead is used as one of the metals to form a thermo couple with other metal because ________ . |
|
Answer» It is a HARD metal |
|
| 44831. |
The focal length of a thin convex lens for red and violet colour are 44.6cm and 42.5cm. Calculate focal length for the mean colour and dispersive powerof the lens. |
|
Answer» FOCAL LENGTH `=43.53cm` DISPERSIVE power `=0.048` `f=sqrt(44.6xx45.5)=43.53cm` `:.` Dispersive power `=(f_(r)-f(v))/f=(44.6-42.5)/43.33=0.048` |
|
| 44832. |
Define current sensitivity of a galvanometer. |
| Answer» SOLUTION :The NUMBER of divisions to which a given MCG gets deflected per one ampere of CURRENT in it is known as the current sensitivity of MCG | |
| 44833. |
(A):A metal ball and a wooden ball of same radius are dropped from the same height in vaccum reach the ground same time. (R ):In vacuum all the bodies dropped from same height take same time to reach the round. |
|
Answer» |
|
| 44834. |
A string having linear density 1.96xx10^3kg/m is subjected to a load of 2kg. Then the velocity of the transverse waves through it , |
|
Answer» 50m/s |
|
| 44835. |
The velocity of a transverse wave in a string depends upon |
|
Answer» LENGTH of the STRING |
|
| 44836. |
Find out total energy stored in the capacitors. |
|
Answer» `500 MU J ` |
|
| 44837. |
What type of charge carriers are there in an n-type semiconductor ? |
| Answer» SOLUTION :In n-type semiconductor, the ELECTRONS are the majority carriers while HOLES are minority carriers. | |
| 44838. |
A circuit consists of three batteries of emf E_1 = 1 V, E_2= 2 V and E_3 = 3 V and internal resistances 1 Omega ,2Omega and 1 Omega respectively which are connected in parallel as shown in the figure. The potential difference between points P and Q is |
|
Answer» Solution :Here ` E_1= 1 V, E_2=2 V ,E_3 =3V` ` r_1=1Omega, r_2= 2 Omega, r_3= 1 Omega` theeffectiveemfof thecircuitis ` E_("EFF")=((E_1)/( r_1)+(E_2)/(r_2) +(E_3)/(r_3))/((1)/(r_1) +(1)/(r_2) +(1)/(r_3) )= ((1)/(1) +(2)/(2) +3/1)/(1/1 +1/2 + 1/1 )= ( (10)/(2) )/(5/2) = 10/5 =2 V ` ` THEREFORE `potentialdifferencebetweenpointsP and Q` = E_("eff") = 2V ` |
|
| 44839. |
A wave of frequency 100Hz is sent along a string towards a fixed end. When this wave travles back then after reflection, a node is formed at a minimum distance of 10 cm from the fixed end of the string. The speed of the incident wave is |
|
Answer» 40 m/s |
|
| 44840. |
Two concentric shells of radii R and 2 R are shown in (Fig. 3.115). Initially, a charge q is imparted to the inner shells. Now, key K_1 is closed and opened and then key K_2 is closed and opened. After the keys K_1 and K_2 are alterbately closed n times each, find the potential difference between the shells. Note that finally key K_2 remains closed. . |
|
Answer» Potential due to charge on the inner sphere and that due to charge on the outer sphere is `V'_1 = (1)/(4 pi epsilon_0)[Q/(2 R) + (q'_1)/(2 R)] = 0` or `q'_1 = -q` When `K_2` is closed first time, the potential `V'_2` on the inner sphere becomes zero as it earthed. Let the new charge on the inner sphere be`q'_2`. `0 = (1)/(4 pi epsilon_0) (q'_2)/(R)+ (1)/(4 pi epsilon_0) ((- q))/((2 R))` or `q'_2 = q/(2)` Now, when `K_1` will be closed second time, charge on the outer sphere will be `-q'_2`, i.e., `- q//2`. After one event involving CLOSURE and OPENING of `K_1` and `K_2`, charge is reduced to half of its initial value. Similarly, when `K_1` will be closed `n^(th)` time, charge on the outer sphere will be `-q //(2^(n - 1))` as each time charge will be reduced to half of the previous value. After closing `K_2 n^(th)` time, charge on the inner shell will be negative of half the charge on the outer shell, i.e., `(+ q//2^n)` and potential on it will be zero. For potential of the outer shell `V_0 = (1)/(4 pi epsilon_0) ((+ q //2^n))/(2 R) + (1)/(4 pi epsilon_0) ((-q //2^(n - 1)))/(2 R)` =`(- q[- 1 + 2])/(4 pi epsilon_0 2^(n +1) R)= (-q)/(4 pi epsilon_0 2^(n -1) R)` Potential difference is `V_0 - V_i = (-q)/(4 pi epsilon_0 2^(n+1) R) - 0 = (-q)/(4 pi epsilon_0 2^(n + 1) R)`. |
|
| 44841. |
A charge Q is divided into two parts of q and (Q-q) . If the Coulombian repulsion between them, when they are separated by a finite distance, is maximum the ratio(q)/(Q)should be ____________ |
|
Answer» |
|
| 44842. |
Why are the wires that carry equal currents are often twisted together ? |
|
Answer» Solution :DUE to average distance is practically same. current FLOWS in two WIRES in OPPOSITE directions. |
|
| 44843. |
A point source emits 30.0 W of sound isotropically. A small microphone intercepts the sound in an area of 0.750 cm?, 180 m from the source. Calculate (a) the sound intensity there and (b) the power intercepted by the microphone |
| Answer» SOLUTION :`(a) 7.37 xx 10^(-5) W//m^2 , (B) 5.53 xx 10^(-9) W` | |
| 44844. |
A coil of self -inductance L and resistance R is connected to a resistance R and a cell of emf E as shown. The switch is kept closed for a long time and then opened. The heat produced in the coil, after opening the switch is |
|
Answer» `LE^(2)//2R^(2)` |
|
| 44845. |
A long straight current carrying wire passes normally through the centre of circular loop. If the current through the wire increases, will there be an induced emf in the loop ? Justify. |
| Answer» SOLUTION :When current FLOWING through a long straight current carrying wire increases, the magnetic field `vceB` increases. However, the magnetic field `vceB` ACTS radially along the loop and the magnetic flux associated to the loop `phi_(B) = vceB. vceA = BA COS 90^(@) = 0`. So, there is no induced emf in the loop. | |
| 44846. |
Equivalent resistance across A and B in the given circuit is |
|
Answer» 7R |
|
| 44847. |
A 280 day old radioactive substances shows an activity of 6000 dps, 140 days later its activity becomes 3000 dps. What was its initial activity ? |
|
Answer» 20000 DPS |
|
| 44848. |
The figure showsa schematic diagram showing the arrangements of Young's Double slit Experiment if the distance d is varied ,then identify the correct statement |
|
Answer» The angular width does not CHANGE |
|
| 44849. |
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is |
|
Answer» `2:3` |
|
| 44850. |
P=mv |
Answer» SOLUTION :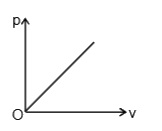
|
|