Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 39201. |
Explain how Newton verified his law of gravitation. |
|
Answer» Solution :The gravitational force EXPERIENCED by the apple DUE to Earth. `F=-(GM_(E)M_(A))/(R^2)` `M_(A)` - Mass of the apple, `M_(E)` - Mass of the Earth and R - Radius of the Earth. Equating the above equation with Newton's SECOND law, we get `M_(A)a_(A)=-(GM_(E)M_(A))/(R^2)` Simplifying the above equation we get, `a_(A)=-(GM_(E))/(R^2)` `a_(A)` is the acceleration of apple that it equal to 'g'. Similarly the force experienced by Moon due to Earth is given by `F=-(GM_(E)Mm)/(R_(m)^(2))` `R_(m)` - distance of the Moon from the Earth, `M_(m)` - Mass of the Moon. The acceleration experienced by the Moon is given by, `a_(m)=-(GM_(E))/(R_(m)^(2))` The ratio between the apple's acceleration to Moon's acceleration is given by `(a_A)/(a_m)=(R_(m)^(2))/(R^2)` From the Hipparchrus MEASUREMENT, the distance to the Moon is 60 times that of Earth radius. `R_(m)=60R` `(a_(A))/(a_(m))=((60R)^(2))/(R^2)=3600` The apples's acceleration is 3600 times the acceleration of the Moon. The same result was obtained by Newton USING his gravitational formula. |
|
| 39202. |
A bullet of mass 10 g and speed 500m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it. |
|
Answer» SOLUTION :The moment of inertia of the door about the VERTICAL axis at ONE end is `ML^(2)//3` 0.625 rad/s |
|
| 39203. |
A uniform rod of length 2m and mass 5kg is lying on a horizontal surface. The work done in raising one end of the rod with the other end in contact with the surface until the rod makes an angle 30^(@) with the horizontal is, (g= 10 ms^(-2)) |
| Answer» ANSWER :A | |
| 39204. |
There is a thin rod of uniform cross-section of mass M and length L. If this rodis is bent at 90^(@) from the mid-point, then the moment of inertia about the axis passing through mid-point and perpendicular to the plane which includes both parts of rod is ......... |
|
Answer» `(ML^(2))/(24)`  After the ROD bent at right angle mass of its energy part = `(M)/(2)` Length of every part = `(L)/(2)` Now total moment of inertia, I = sum of moment of inertia of both the part `therefore I=(1)/(3)((M)/(2))((L)/(2))^(2)+(1)/(3)((M)/(2))((L)/(2))^(2)` `=2((1)/(3)((M)/(2))((L)/(2))^(2))` `therefore I=(ML^(2))/(12)` |
|
| 39205. |
Water is flowing through a horizontal tube of length 0.25 m and radius4xx 10 ^(-4) m under a constant pressure head of 0.2 m of water, at the rate of 5 xx 10 ^(-6) m^(3) per minutre . Calculate the coefficient of visosity of water. Density of water = 1000 kg m^(-3) |
|
Answer» Solution :` "" l = 0.25 m, r- 4 xx 10 ^(-4) m ` ` ""P= h rho g =0.2 m " ofwater"= 0.2 xx 10 ^(3)xx 9.8 Pa` Volume ` V = 5 xx 10 ^(-6)m^(3)` ` "" t= ` one minute = 60S ` eta = ? ` ` Q = ( V)/(t)= (pi P r^(4))/( 8 eta l) ` ` eta = ( pi h rho g r^(4) t)/( gl V) ` `= (3.14 xx 0.2 xx 10 ^(-3)xx 9.8 xx ( 4 xx 10 ^(-4) ) ^(4) xx 60 )/( 8 xx 0.25 xx 5 xx 10 ^(-6)) ` `= 0 .000945 N s m^(-2)` |
|
| 39206. |
Water is flowing in streamline motion throw a tube with its axis horizontal consider two point A & B in the tube at the same horizontal levels |
|
Answer» the pressure at A & B are equal for any shape of the tube |
|
| 39207. |
In one dimensional motion, instantaneous speed V satisfies 0 le V lt V_(0). |
|
Answer» The displacement in TIME T MUST ALWAYS take nonnegative values. |
|
| 39208. |
The magnitude of distance is always |
|
Answer» POSITIVE |
|
| 39209. |
In case of a forced vibration, the resonance wave becomes very sharp when the : |
|
Answer» applied periodic force is SMALL quality factor is small 
|
|
| 39210. |
A bodyof mass 1 kg makes an elastic collision with another body at rest and continues to move in the original direction after collision with a velocity equal to 1/5th of its original velocity. Find the mass of the second body. |
|
Answer» `(2)/(3) KG` |
|
| 39211. |
A Ship .A. steams down north at a speed of 8 kmph. And ship B due west at a speed of 6 kmph. The velocity of A w.r.t. B is. |
|
Answer» 10 KMPH, `Tan^(-1)((4)/(3))N` of E |
|
| 39212. |
The path length can be equal to or ........... than the displacement. |
|
Answer» less |
|
| 39213. |
Given noticeable points, about the amplitude of resultant waves of two harmonic progressive waves on stretached string. |
|
Answer» Solution :The amplitude of RESULTANT wave is a function of phase difference `phi` between TWO element waves. `A (phi) =2 a cos "" (phi)/(2)` When two waves have same phase, then `phi =0 ` HENCE,` y (x,t) =2a sin (KX - omega t )` Relultant amplitude is `A = 2a. `It is maximum amplitude. If `phi =PI` the two waves are completely out of phase, the amplitude of the resultant wave reduces to zero. `therefore (x ,t)= 0 [because A (phi) = 2 cos "" (phi)/(2) = 2 a cos "" (pi)/(2) =0]` |
|
| 39214. |
A uniform chain of length 'L' and mass 'm' is on a smooth horizontal table, with (1)/(n) th part of its length hanging from the edge of the table. Find the kinetic energy of the chain as it completely slips off the table |
|
Answer» SOLUTION :With respect to the top of the table, the initial potential energy of the chain `U_(1)`= PF of the chain lying on the table + PE of the hanging part of the chain `= L (1- (1)/(n)) mg (0)(m)/(n)G (-(L)/(2n))= - (MGL)/(2n^(2))` P.E of the chain, when it just slips off the table. `U_(2)= mg ((-L)/(2)) = - (mgL)/(2)` From LAW of conservation of energy `Delta K= - Delta U K_(r)- K_(i) = - (U_(f)- U_(i))` `because K_(i)= 0, K_(f)= - [-(mgL)/(2)- (-(mgL)/(2n^(2)))]`  If .V. is the velocity of the chain, then, `(1)/(2) mv^(2)= (mgL)/(2) [1-(1)/(n^(2))]` 
|
|
| 39215. |
The acceleration of a car is 10 mile per hour per second. The same is (ft)//(s^(2)) is |
|
Answer» `1.467(ft)/(s^(2))` or `(10"mile")/("hour SECOND")=n_(2)(ft)/(s^(2))` or `(10xx1760xx3ft)/(60xx60s^(2))=n_(2)(ft)/(s^(2))` `:. n_(2)=1.467ft//s^(2)` |
|
| 39216. |
If two objects A and B are moving along a straight line in the opposite direction with the velocities V_(A)andV_(B) respectively, then relative velocity is |
|
Answer» `V_(A)+V_(B)` |
|
| 39217. |
A spacecraft is in a circular orbitof radius 3R around the moon as shown in figure-6.109. At point A, the spacraft fires a probe which is supposed to arrive at the surface of the moon at point B. Datermine the necessary velocity v_(r) of the probe relative to the spacecraft just fter ejection. Also calculate the angular displacement theta of the spacecraft when the probe arrives at point B. Assume velocity of spacecraft remains unchanged due to ejection of probe. |
|
Answer» |
|
| 39218. |
If excess pressure is balanced by a column of oil (with specific gravity 0.8) 4 mm high, where R = 2.0 cm, Find the surface tension of the soap bubble. |
|
Answer» <P> Solution :The excess of pressure inside the SOAP bubble is`"" DeltaP = P_(2) - P_(1) = (4T)/R` But `"" DeltaP = P_1 - P_1 = rho GH implies rho gh = (4T)/R` `implies "surface tension" , T = (rho gh R)/4 = ((800)(9.8)(4 XX 10^(-3))(2 xx 10^(-2)))/(4)` `T = 15.68 xx 10^(-2) Nm^(-1)` |
|
| 39219. |
For a given material, the rigidity modulus is ((1)/(3))^(rd) of Young's modulus. Its Poisson's ratio is |
|
Answer» 0 `eta = Y/(2(1 - sigma))sigma` - Poisson.s ratio Here, `"" eta1/3 y implies 3 eta = y` Substituting the value, we GET `sigma = 0.5` |
|
| 39220. |
The rate of leak from a hole in a tank is ………………. . |
|
Answer» independent of its height from the bottom |
|
| 39221. |
Calculate the efficiency of an engine whose working substance absorbs 3000 J of heat from the source and rejects 2000 J of heat to the sink. |
|
Answer» Solution :Heat ABSORBED from the SOURE `= Q_(1) = 3000 J` Heat rejected to the SINK` = Q_(2) = 2000 J` Efficiency `= ETA ( Q_(1) - Q_(2))/( Q_(2))= ( 3000 - 2000)/( 2000) = 0.5 = 50%` |
|
| 39222. |
What is the maximum magnitude of change in velocity of a motor cycle moving with uniform speed V_(0) in a circular path of length l= (piR)/(3) and radius R |
| Answer» Answer :A | |
| 39223. |
Explain Right hand rule to find the direction of Torque. |
| Answer» Solution :If fingers of right hand are kept along the POSITION VECTOR with palm facing the direction of the force and when the fingers are CURLED the thumb POINTS to the direction of the TORQUE. | |
| 39224. |
Answer with reason: In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time ofcollision of the balls (i.e., when they are in contact )? |
| Answer» SOLUTION :The collision produces a SLIGHT deformation of both the balls. A partof the KE is used for that deformation , so the total KE is not CONSERVED during the short time of collision. However,due to the elastic stress DEVELOPED in the perfectly elastic balls, the kinetic ENERGY is regained after the collision. | |
| 39225. |
A stone is thrown upward from a moving train. A man can jump on moon six times as high as on earth. Why? |
| Answer» SOLUTION :`Hpropto1/g` .The acceleration due to gravity at the SURFACE of the MOON is nearly `1^(th)/6` of that at the earth’s surface | |
| 39226. |
A man isswimming against current such that his position with respect to the river bank remains unaltered.Is the man doing any work ? |
| Answer» Solution :The relative DISPLACEMENT of the man with respect to the river BANK is zero . So, no WORK is done by the man. The resistive force of river water just BALANCES the force applied by the man . So, this case is similar to a force applied against static FRICTION. | |
| 39227. |
The escape velocity of a body from the surface of the earth is nearly |
|
Answer» `7.98 KMS^(-1)` |
|
| 39228. |
A physical quantity P is related to four observables a,b,c and d as follows: P = a^(3)b^(2)/(sqrtcd) The percentage errors of measurement in a,b, c and d are 1%, 3% , 4% and 2% respectively. What is the percentage error in the quantity P ? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result ? |
| Answer» SOLUTION :13%, 3.8 | |
| 39229. |
Resultant of two vector of equal magnitude A is |
|
Answer» `sqrt(3)Aat 60^(@)` |
|
| 39230. |
A body falls freely from a height 'h' its average velocity when it reaches earth is |
|
Answer» `SQRT(gh)` |
|
| 39231. |
An ideal refrigerator has a freezer at a temperature of -13∘C. The coefficient of performance of the engine is 5. The temperature ofthe air (to which heat is rejected) will be |
| Answer» ANSWER :C | |
| 39232. |
A bullet hits and gets embedded in a solid block resting on africtionless table. What Is conserved? |
|
Answer» MOMENTUM and K.E |
|
| 39233. |
Two identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string. |
|
Answer» |
|
| 39234. |
In the given (V-T) diagram, what is the relation between pressures P_(1) and P_(2) ? |
|
Answer» `P_(2) gt P_(1)` PV = nRT or `V = (nRT)/(P)` For an isobaric process, P = constant and `V prop T` Therefore, V - T graph is a straight line passing through origin. SLOPE of this line is inversely proportional to P. In the given figure, `("Slope")_(2) gt ("Slope")_(1) :. P_(2) lt P_(1)` 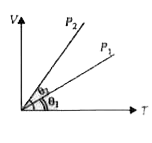
|
|
| 39235. |
The period of oscillation of a simple pendulum is T =2pisqrt(L/g). Measuted value of L is 20.0 cm known to 1mm accuracy and time for 100 oscillations of the pendulum is found to be 90s using a wrist watch of 1 s resolution. What is the accuracy in the determination of g ? |
|
Answer» Solution :`g= 4PI^(2) L//T^(2)` Here, `T= (T)/(n) and Delta T = (Delta t)/( n)`. THEREFORE, `(Delta T)/( T) = (Delta t)/( t)`. The errors in both L and t are the least count errors. Therefore, `(Deltag //g) = (Delta L//L) + 2(Delta T//T)` `= (0.1)/( 20.0) +2 ((1)/(90) ) = 0.027` Thus, the percentage ERROR in g is `100 (Delta g//g) = 100(Delta L//L) + 2 XX 100 (Delta T //T) = 3` |
|
| 39236. |
A vector is not changed if |
|
Answer» it is rotated through an arbitrary angle |
|
| 39237. |
In experiment to measure density of a subtance mass m=(3+-0.12) kg and volume V=(10+-1)m^(3) recorded. Find relative error in measurement of density (rho=(m)/(V)) |
|
Answer» SOLUTION :`rho=(m)/(V)` Relative ERROR in measured density `=(Deltarho)/(rho)` `=(DELTAM)/(m)+(DeltaV)/(V)=(0.12)/(3)+(1)/(10)=0.04+0.1=0.14` Percentage error =Relative error `xx100` `=0.014xx100%=14%` |
|
| 39238. |
We know that the density of a cube can be measured by measuring its mass and length of its side. If the maximum errors in the measurement of mass and length are 3% and 2% respectively, what is the maximum error in the measurement of the density of the cube? |
|
Answer» |
|
| 39239. |
Viscous force acting between two layers of liquid having area A and velocity gradient (Deltav)/(Deltaz) is given by F = etaA(Deltav)/(Deltaz) . Find dimension of eta. |
|
Answer» `M^(1)L^(-2)T^(-2)` `:. ETA=(FDeltav)/(ADeltaz) "" DeltaV`= velocity `:.[eta]=([F][Deltaz])/([A][Deltav])` `=((M^(1)L^(1)T^(-2))(M^(0)L^(1)T^(0)))/((M^(0)L^(2)T^(0))(M^(0)L^(1)T^(-1)))` `=M^(1)L^(-1)T^(-1)` |
|
| 39240. |
An artificial satellite of mass 500 kg revolve around the earth, its angular momentum 4xx10^(7)Js. What will its Ariel velocity? |
|
Answer» `2XX10^(4)m^(2)s^(-1)` |
|
| 39241. |
A force is applied on a body of mass 0.9kg that is at rest. The force is applied for a duration of 5s and as a result the body covers distance of 250m . Find the magnitude of the force. |
|
Answer» |
|
| 39242. |
In a circus the diameter of the globe of depth is 20 m calculate the minimum heightmust a cyclist start in order to go round the globesuccessfully |
|
Answer» Solution :Whenthe cyclistrollsdownthe inciline `mgh = (1)/(2)MV^(2)` `:.`velocitygained`v=SQRT(2gh)` forloopingthe loopthe minimumvelocityat THELOWEST point`=sqrt(5gr)` `h= (5r)/(2 )` `=(5)/(2) XX (10) =25 m` Heightof thecyclist `=25` m |
|
| 39243. |
A particle of mass m strikes a smooth floor with speed u at angle of incidence theta with the normal. The coefficient of resultant is e. Find the magnitude and direction of velocity with which the particle rebounds. Also, find the impulse and loss in K.E. |
|
Answer» Solution :Before the collision: After the collision: Since there is no force ALONG the surface , hence the velocity component remains same. `V sin alpha = u sin theta`(i) Due to the normal force between the particle and the floor , the velocity component becomes `e TIMES` in opposite direction `v cos alpha = e u cos theta`(II) `v = sqrt((v sin alpha)^(2) + (v cos alpha)^(2)) = u sqrt(sin^(2) theta + e^(2) cos^(2) theta)` `tan alpha = ( v sin alpha)/(v cos alpha) = (1)/(e) tan theta` If the collision is elastic , `e = 1 , v = u , alpha = theta` `J_(x) = 0` `J_(y) = m(v cos alpha + u cos theta)` `= m ( e u cos theta + u cos theta) = mu cos theta ( 1 + e)` `J = mu cos theta ( 1 + e)` `Delta K = (1)/(2) mu^(2) - (1)/(2) m u^(2)= (1)/(2) mu^(2) cos^(2) theta ( 1 - e^(2))` `Delta` K: loss in `K.E.`  
|
|
| 39244. |
A cylindrical block of length 0.4 m and area of cross-section 0.04m^(2) is placed coaxially on a thin metal disc of mass 0.4kg and of the same cross section. The upper face of the cylinder is maintained at constant temperature of 400 K and the initial temperature of the disk is 300K. If the thermal conductivity of the material of the cylinder is 1" wm"^(-1)K^(-1) and the specific heat of the material of the disk is 600 j\kg -K, how long will it take for the temperature of the disc to increase to 350 K. (Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder) |
|
Answer» 190 s |
|
| 39245. |
An ideal gas is trapped between a mercury columnand the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to the atmosphere. (Atmospheric pressure is 76 cm of mercury). The length of the mercury and the trapped gas columns are 20 cm and 43 cm, respectively. What will be the length of the gas column when the tube is tilted slowly in a vertical plane through an angle of 60^(@). Assume the temperature to be constant. |
|
Answer» <P> Solution :Boyle.s law HOLDS GOOD because the TEMPERATURE is constant.So, `P_(1)V_(1)=P_(2)V_(2)" or "P_(1)l_(1)=P_(2)l_(2)` , since the bore is uniform `P_(1)=76+20=96 cm` of Hg , `l_(1)=43 cm, P_(2)=76+h=76+20cos60^(@)=76+10=86cm` of Hg `l_(2)=?` `THEREFORE 96 times 43=86l_(2)` `therefore l_(2)=48cm` of Hg |
|
| 39246. |
Read the following two statements below carefully and state, with reasons, if is true or false. (a) The Young's modulus of rubber is greater than of steel , (b) The stretching of a coil is determined by shear modulus. |
|
Answer» |
|
| 39247. |
Two smooth spheres A and B, of equal radius but masses m and M, are free to move on a horizontal table. A is projected with speed u towards B which is at rest. On impact, the line joining their centres is inclined at an angle theta to the velocity of A before impact. If e is the coefficient of restitution between the spheres, find the speed with which B begins to move. If A.s path after impact is perpendicular to its path before impact, show that tan ^(2) theta = (eM-m)/(M +m). |
|
Answer» SOLUTION :When B is struck by the impulse J, it BEGINS to MOVE in the direction of J as shown in the . Along the line of centres, we apply (a) Conservation of linerar momentum , i.e., `m u cos theta MV - mv …(1)` (b) Law of resistution, i.e., `eu cos theta = V +v ...(2)` Solving EQS. (1) and (2) we get `v = ((eM - m) u cos theta )/( (M +m))and V = ((1 + e ) m u cos theta)/( (M + m ))` Hence, `tan phi= ( u sin theta)/( v ) = ((M + m ) tan theta)/( (e M - n ))` Butthe paths of A before and after IMPACT are at rigth angles, therefore,` cot phi = tan theta.` Hence, `((eM - m ))/( (M + m ) tan theta ) = tan theta` `therefore tan ^(2) theta = (eM - m )/( (M + m ))` |
|
| 39248. |
A constant force actson a body of mass m_(1) at rest and produces a velocity 'v' over a displacement 's_(1)'. The same force acts on another body of mass m_(2) at rest and produced the same velocity. 'v' over a displacement 's_(2)'. The ratio of the displacements is |
|
Answer» `m_(1):m_(2)` |
|
| 39249. |
Two points are taken on a massless wire OC, such that OA = AB = BC. Three bodies of equal mass are tied at the points A, B and C and the system is kept on a horizontal smooth table. Keeping the wire taut, if the system is rotated around the point O, then what will be the ratio of tensions in the three parts of the wire? |
|
Answer» |
|
| 39250. |
A particle of mass m is executing SHM about the origin on X-axis with frequency sqrt((ka)/(p m)) ,where k is a constant and a is the amplitude. Find its potential energy, if x is the displacement at time t |
|
Answer» `kax^2` |
|