Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 4401. |
Find the ratio in which the line joining the points (6, 12) and (4, 9) is divided by the curve x^(2)+y^(2)=4. |
|
Answer» |
|
| 4402. |
Match the following from List - I to List - II {:("List-I","List-II"),((I)|{:(1,1,1),(a,b,c),(bc,ca,ab):}|=,(a)(a-b)(b-c)(c-a)),((II)|{:(a,b,c),(a^(2),b^(2),c^(2)),(a^(3),b^(3),c^(3)):}|=,(b)(a-b)(b-c)(c-a)abc),((III)|{:(1,1,1),(a,b,c),(a^(3),b^(3),c^(3)):}|=,(c)(a-b)(b-c)(c-a)(a+b+c)):} |
| Answer» Answer :C | |
| 4403. |
If A and B are two events such that P(barA)=(3)/(4),P((A)/(B))=(1)/(2)andP((B)/(A))=(2)/(3)then P(B)is: |
|
Answer» `(1)/(3)` |
|
| 4404. |
State true of false for the following: the inequality |z-4| lt |z-2| represents the region given by x gt 3 |
|
Answer» |
|
| 4405. |
Centroid of triangle formed by feet of perpendicular from (-3,-6,-9) on coordinate axesis |
|
Answer» (-1,-2,-3) |
|
| 4406. |
Sides of Delta ABC " are in A.P. if " a ltmin {b, c},then cosA may be equal to |
|
Answer» `(4B - 3c)/(2B)` |
|
| 4407. |
Using definition , find the derivative of f(x)=sinsqrt(x). |
|
Answer» |
|
| 4408. |
If bara=4bari+5barj-bark, barb=bari-4barj+5bark, barc=3bari+barj-bark such thatbarpbotbara,barpbotbarb and barp.barc=21 , thenbarp= |
|
Answer» `6(bari+barj+bark)` |
|
| 4409. |
A card is drawn at random froma well-shuffled pack of 52 cards. Find the probability that it is neither aking nor a heart. |
|
Answer» |
|
| 4410. |
Find the slope of the line joining the points (a cos theta , b sin theta) and (a cos phi, b sin phi) |
| Answer» SOLUTION :`(B(SIN THETA - sin phi))/(a (cos theta - cos phi))` | |
| 4411. |
If the lines x+2ay+a=0, x+3by+b=0, x+4cy+c=0 are concurrent, then a, b, c are in |
|
Answer» A.P |
|
| 4412. |
A line passes thorough (x_(1) , y_(1) ) and (h, k). If slope of the line is m, show that, k-y_1 = m(h-x_1). |
|
Answer» |
|
| 4413. |
Derive function of 120^(@)from functions of 60^(@) andcheck by using relations between functions of supplementary angles. |
|
Answer» |
|
| 4415. |
Consider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15,-19), and R(1,-7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0 The radius of the incircle of triangle PQR is |
|
Answer» 4 |
|
| 4416. |
Consider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15,-19), and R(1,-7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0 The sum a+c is |
|
Answer» 129 |
|
| 4417. |
Consider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15,-19), and R(1,-7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0 The distance between the orthocenter and the circumcenter of triangle PQR is |
|
Answer» `25//2` |
|
| 4418. |
Complete the following table (##ANE_PMP_MAT_0XI_C11_E03_028_Q01##) |
|
Answer» Solution :[SUM of local DISTANCES of any POINT : `12,4,1/2 e:sqrt11/6,1/2,3/5` latus RECTUM `25/3,3,8/25` |
|
| 4419. |
The position vectors of the three non-collinear points A, B, C, are bara, barb, barc respectively. The distance of the origin from the plane through A, B, C is |
|
Answer» `[bara BARB barc]` |
|
| 4420. |
Refer to question 6 above, state true or false : (give reason for your answer) A and B are mutually exclusive. |
|
Answer» |
|
| 4421. |
Refer to question 6 above, state true or false : (give reason for your answer) A and B are mutually exclusive and exhaustive |
|
Answer» |
|
| 4422. |
If the range of the function f(x)=((1+x+x^(2))(1+x^(4)))/(x^(3)) when x gt 0 is [K, oo) then K is |
|
Answer» |
|
| 4423. |
If 4 cos theta - 3 sec theta = tantheta, " then " theta= |
|
Answer» `THETA = n PI + (-1)^(n) BETA , n in Z " where SIN " beta = (1 + sqrt(17))/(8)` |
|
| 4425. |
Examine the nature of the roots of the equations (i) 2x^(2)+2x+3=0 (ii) 2x^(2)-7x+3=0 (iii) x^(2)_5x-2=0 (iv) 4x^(2)-4x+1=0 |
|
Answer» |
|
| 4426. |
If the position vectors of A,Band C are respectively 2bari-barj+bark, bari -3barj-5bark and 3bari - 4barj - 4bark, " then " cos^(2)A = |
|
Answer» 0 |
|
| 4427. |
x + 2y le 10,x + y ge 1,x-y le 0,x ge 0, yge 0 |
Answer» 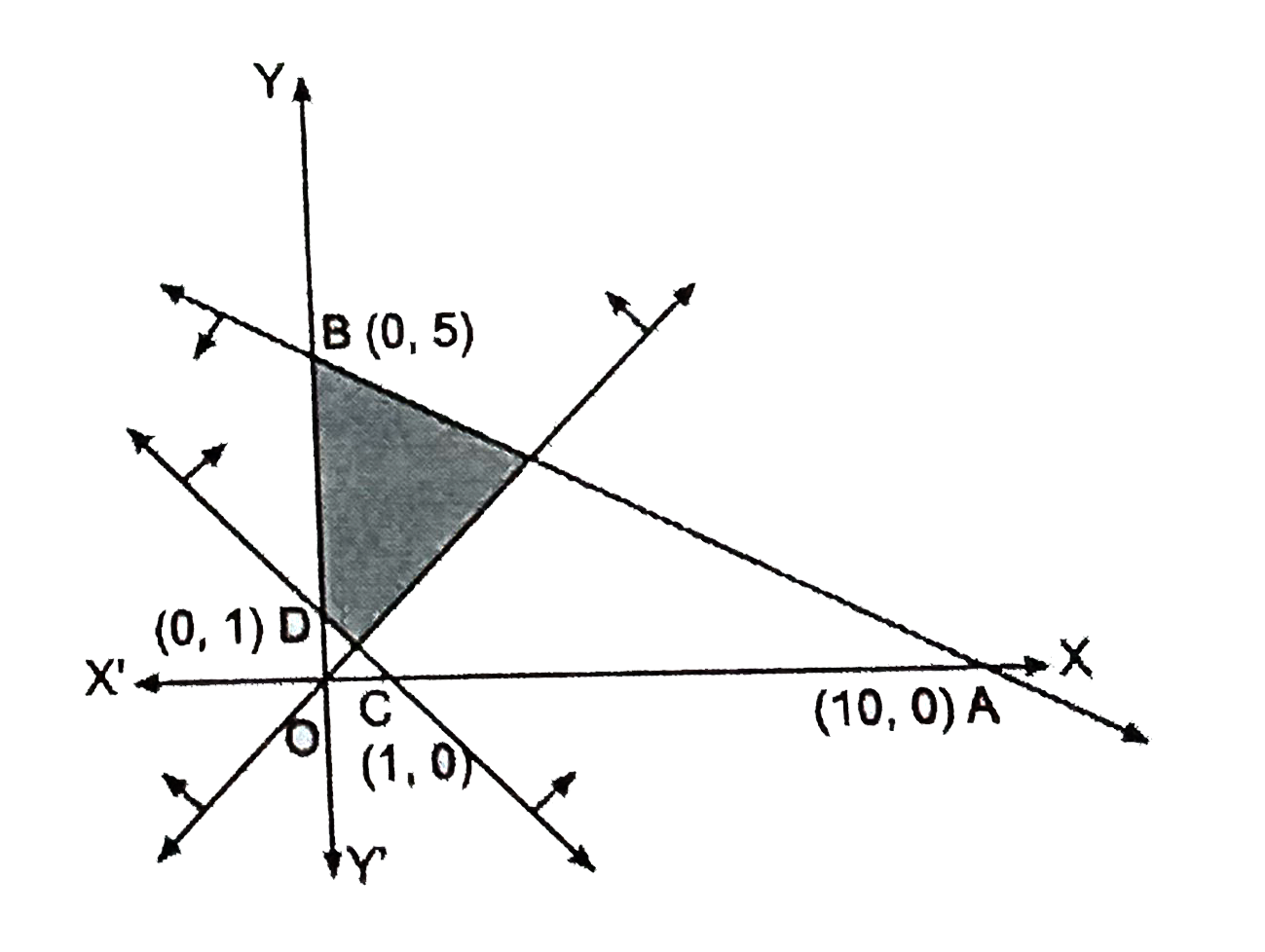
|
|
| 4428. |
If y^2 = p(x) , a polyomial of degree 3 , then 2(d)/(dx)(y^3(d^2y)/(dx^2)) is equal to |
|
Answer» `p^(111)(X)+p^(1)(x)` |
|
| 4429. |
Consider the system of equations sin x cos 2 y = (a ^(2) - 1)^(2) + 1, cos x sin 2 y = a = 1The number of values of y in [0, 2 pi] , when the systemhas solution for permissiblevalues of a is/ are |
|
Answer» 2 |
|
| 4430. |
IfA(n, n^2) (where n in N) is any point in the interior of the quadrilateralformed by x=0, y=0, 3x+y-4=0 and 4x+y-20=0 then the possible number of position of A is |
|
Answer» |
|
| 4431. |
The lines 2x+3y=6, 2x+3y=8 cut the X-axis at A, B respectively. A line l drawn through the point (2, 2) meets the X-axis at C in such a way that abscissae of A, B and C are in arithmetic progression. Then the equation of the line l is |
|
Answer» `2x+3y=10` |
|
| 4432. |
The product of the perpendiculars drawn from the points pm sqrt(a^(2) -b^(2),0) on the line x/a cos theta+ y/b sin theta =1, is |
|
Answer» `a^(2)` |
|
| 4433. |
If alpha,beta are the roots of the equation 3x^(2)-6x+4=0, find the value of ((alpha)/(beta)+(beta)/(alpha))+2((1)/(alpha)+(1)/(beta))+3alphabeta. |
|
Answer» |
|
| 4435. |
If x = a (t + sin t), y= a (1- cost) and (dx)/(dy) =cotp then p = |
|
Answer» t |
|
| 4436. |
If sin A = (1)/(sqrt3) and sin B = (1)/(sqrt5)find the value oftan ""(1)/(2) (A + B) . Cot "" (1)/(2) (A-B). |
|
Answer» |
|
| 4437. |
Cot^(-1)3+Cot^(-1)7+Cot^(-1)13+……n terms = |
|
Answer» `TAN^(-1)(N/(n+2))` |
|
| 4438. |
Which of the following is true for z=(3+2i sin theta)//(1-2 i sin theta), where i=sqrt(-1)? |
|
Answer» Z is purely imaginary for `theta=N PI+-pi//3,n in Z` |
|
| 4439. |
Find the eccentricity of the ellipse whose latus rectum is 4 and distance of the vertex from the nearest focus is 1.5 cm. |
|
Answer» |
|
| 4440. |
Let f(x) = 2^(2x - 1) and phi(x) = -2^(x) + 2x "log" 2. If f'(x) gt phi'(x), then |
| Answer» Answer :C | |
| 4441. |
The most general value of x for which sinx+cosx= "min"_(a in R) {1, a^(2)-4a+6} are given by |
|
Answer» `2n pi+(pi)/(6)` |
|
| 4442. |
If f(x+y)=f(x)f(y) for all x and y if f(1)=2, then area enclosed by 3absx+2absyle8 is |
|
Answer» `f(5)sq.units` |
|
| 4443. |
If thetainQ_(3) , then sqrt(4sin^4theta+sin^(2)2theta)+4cos^2(pi/4-theta/2)= |
|
Answer» 2 |
|
| 4445. |
Let the lines represented by equation x^2y^2-y^2+1=0 form a square ABCD. A point 'P' is taken on the same plane of square such that atleast two sides of all the triangles PAB, PBC,PCD and PDA are equal. The number of possible position of th point 'P' |
|
Answer» 1 |
|
| 4446. |
Let the lines represented by equation x^2y^2-y^2+1=0 form a square ABCD. A point 'P' is taken on the same plane of square such that atleast two sides of all the triangles PAB, PBC,PCD and PDA are equal. For all the possible position of the 'P' . The number of the given triangles have all the three side equal |
|
Answer» 0 |
|
| 4447. |
Let the lines represented by equation x^2y^2-y^2+1=0 form a square ABCD. A point 'P' is taken on the same plane of square such that atleast two sides of all the triangles PAB, PBC,PCD and PDA are equal. One of the possible position of the 'P' such that atleast one of the given triangle is equilateral given by |
|
Answer» (0,0) |
|
| 4448. |
For specifying a straight line, how many geometrical parameters should be known ? |
|
Answer» `1` |
|
| 4449. |
f(x) = (tan^(-1) (x +2))/(|x =2|) , x ne -2 " and " f(-2) =-1 then at x = -2 , f is |
|
Answer» LEFT CONTINUOUS |
|
| 4450. |
Let f(x)=(x-3)^(5)(x+1)^(4) then |
|
Answer» `x=7//9`is a POINT of maxima |
|