Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1301. |
The ratio of boys and girls in a certain class is 5:4 If 4 boys and 4 girls are added, the ratio would be 6:5 . Find the number of boys and girls in the class. |
|
Answer» |
|
| 1302. |
A man invests 1680rs in buying shares of nominal value 24rs and selling at 12% premium. The dividend on the shares is 15% per annum . Calculate (i) the number of shares he buys, (ii) the dividend he receives annually |
|
Answer» |
|
| 1303. |
Choose the correct alternative. (iii) if point P divides segment joining (-5,6) and B (3,-5) in the co-ordinates of points P are |
| Answer» ANSWER :C | |
| 1304. |
If the circumference at the base of a right circular cone and the slant height are 120picm and 10cm respectively, then the curved suface area equal to ……… . |
|
Answer» `1200picm^(2)` |
|
| 1305. |
The volume of a conical tent is 1232 m ^(3) and the area of the base floor is 154 m^(2). Calculate the : radius of the floor, |
|
Answer» |
|
| 1306. |
What is the probability of getting a king when a card is drawn at random from a well-shuffled deck of 52 cards? |
|
Answer» |
|
| 1307. |
A tower stands on a horizontal plane. The shadow of the tower when the angle of the elevation of the Sun is 30^(@) is 45m more than when the angle of elevation of the Sun is 60^(@), Then, the height of the tower is……….m |
|
Answer» `(45 SQRT3)/(2)` |
|
| 1309. |
A man drives his car with uniform speed from place A to the place B which is 150 km away. Again he returns to the place A by increasing the speed of the car 10km/hour and there by reaches 30 minutes earlier than the time taken in his forward journey. find the total time taken by him in forward and return journey. OR A, B and P are the three non-collinear points on a plane. The distance between the point A and P is 2m more than the distance between the points B and P. if the distance between points A and B is 10 m and AB is the longest side of the triangle ABC. Is ABC a right angled triangle or not, justify your answer using the discriminant of quadratic equation and also find the measure of AP and BP. |
|
Answer» Or `:.` The SIDE of `DELTAAPB` has a REAL value. |
|
| 1311. |
Find the nature of the roots of the quadratic equations. If real roots exist, find them 2x^(2)-3x+5=0 |
|
Answer» |
|
| 1312. |
A point P is reflected in the x-axis. Co-ordinates of its image are (-4, 5). Find the co-ordinates of the image of P under reflection in the y-axis. |
|
Answer» |
|
| 1314. |
An iron pillar consists of a cylindrical portion of 2.8 m. height and 20 cm. in diameter and a cone of 42 cm. height surmounting it. Find the weight of the pillar if 1 cm^(3) of iron weighs 7.5 g. |
|
Answer» |
|
| 1315. |
At the rate of half -yearly compound interest a sum of money amounts 9261/8000 timesof it then find the rateof interest. |
|
Answer» |
|
| 1316. |
The volume of a conical tent is 1232 m ^(3) and the area of the base floor is 154 m^(2). Calculate the : length of the canvas required to cover this conical tent if its width is 2 m. |
|
Answer» |
|
| 1317. |
Determine the AP whose 3rd term is 5 and the 7th term is 9. |
|
Answer» |
|
| 1318. |
If the median of the distribution given below is 28.5 , find the values of x and y. |
Answer» Solution :  Since the total number of observation is 60 `:. 45+x+y=60rArr x+y=15` Median is GIVEN to be 28.5 so it will fall in the class 20-30 `:. """Median"=l_(1)+(((N)/(2)-C))/(f)xxi` `rArr 28.5=20+(30-(5+x))/(20)xx10` `rArr 57-4025-x` `rArr x=8` Putting the VALUE of x=8 in eq. (1) we get Hence, x=8,y=7 |
|
| 1319. |
Let A=[{:(,5,4),(,3,-2):}], B=[{:(,-3,0),(,1,4):}] and C=[{:(,1,-3),(,0,2):}], find : (i) A+B and B+A (ii) (A+B)+C and A+(B+C) (iii) Is A+B=B+A? (iv) Is (A+B) +C=A+(B+C)? |
|
Answer» (II) `[{:(,3,1),(4,4):}]` |
|
| 1320. |
Choose the number pair/group which is different from others. |
|
Answer» `133-98` |
|
| 1321. |
Find the roots of the following quadratic equations, if they exist. 2x^(2)-2sqrt(2)x+1=0 |
|
Answer» |
|
| 1322. |
Which of the following is a statement? |
|
Answer» 2 is not a PRIME NUMBER. |
|
| 1323. |
Sides of some triangles are given below: (i) 5 cm, 12 cm , 15 cm (ii) 5 cm , 6 cm , 8 cm (iii) 8 cm, 15 cm , 17 cm . Among these, right triangles is : |
| Answer» ANSWER :C | |
| 1324. |
Compare the above surface area with the area of the base of the cone. |
|
Answer» |
|
| 1325. |
Fourth and seventh terms of a G.P. are (1)/(18) and -(1)/(486) respectively. Find the G.P. |
|
Answer» |
|
| 1326. |
Which of the following is an irrational number ? |
|
Answer» `22/7` |
|
| 1327. |
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii. |
|
Answer» |
|
| 1328. |
Find the arithmetic mean of : (i) -5 and 41 (ii) 3x-2y and 3x+2y (iii)) (m+n)^2 and (m-n)^2 |
|
Answer» |
|
| 1329. |
The point P (2, -4) is reflected about the line x = 0 to get the image Q.The point Q is reflected about the line y = 0 to get the image R.Find the area of figure PQR. |
|
Answer» |
|
| 1330. |
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its longer side. |
|
Answer» |
|
| 1331. |
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its shorter side. |
|
Answer» |
|
| 1332. |
Prashant bought 50 shares of FV 100, having MV 180. Company gave 40% dividend on the shares. Find the rate of return on investment. |
|
Answer» |
|
| 1333. |
A card is drawn at random from a well shuffled pack of 52 cards. Find the probability that the card drawn is neither ace nor king. |
|
Answer» |
|
| 1334. |
A card is drawn at random from a well shuffled pack of 52 cards. Find the probability that the card drawn is 10 of spades. |
|
Answer» |
|
| 1335. |
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC. or A circle touches all the four sides of a quadrilateral ABCD. Prove that AB+CD=BC+DA. |
|
Answer» SOLUTION :LET the circle touches the sides AB,BC,CD and DA of a SQUAREABCD at P,Q,R and S respectively. Since, the tangents drawn from an external point to a circle are equal in length. `:.""AP=AS""...(1)` `BP=BQ""...(2)` `CR=CQ""...(3)` and`""DR=DS""...(4)` Adding (1), (2), (3) and (4), we get `ubrace(AP+BP)+ubrace(CR+DR)=AS+BQ+CQ+DS` `implies""AB+CD=(AS+DS)+(BQ+CQ)` `implies""AB+CD=AD+BC""` Hence Proved. 
|
|
| 1336. |
In which direction is Rahul facing? I. In the early morning Rahul was standing in front of a puppet and the shadow of puppet was falling to the right of Rahul. II. In the early morning Rahul was standing on the ground. His shadow was falling behind him when he turned to his left. |
|
Answer» if the data in statement I ALONE are sufficient to answer the question, while the data in statement II alone are not sufficient to answer the question, From I, we know that Rahul and the puppet are facing each other. The shadow of the puppet falls to the right of Rahul and hence to the left of the puppet. Thus, the sun is to the right of the puppet. But the sun is in the East. So, the puppet is facing North and thus, Rahul is facing South.  From II, we know that on turning left the shadow falls behind Rahul. This means that Rahul faces the sun (i.e. East) on turning left. Thus, Rahul is facing South. |
|
| 1337. |
A point P is its own image under the reflection in a line l. Describe the position of the point P with respect to the line l. |
|
Answer» |
|
| 1338. |
Metallic spheres of radii 6cm,8cm and 10cm respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere. |
|
Answer» |
|
| 1339. |
Given that x+2 and x-3 are factors of x^3+ax+b, calculate the values of a and b. |
|
Answer» |
|
| 1340. |
Check whetherthe given pair of equations represent intersecting, parallel or coincident lines. Find the solution if the equations are consistent. 2x + y - 5 = 0 3x - 2y - 4 = 0 |
|
Answer» |
|
| 1341. |
If two tangents to a circle are inclined at an angle of 35^(@), the radit through the points of contact of those tangents are inclined at an angle of .......... |
|
Answer» `35 ^(@)` |
|
| 1342. |
If the tip of the pendulum of a clock travels 13.2cm in one oscillation and the length of the pendulum is 6.3 cm, then the angle covered by the pendulum during this half oscillation in radian system is ___________. |
|
Answer» |
|
| 1343. |
Draw a circle of radius 2 cm . Draw any triangle inside the circle so that the drawn circle be the circumcircle of the triangle. Now, draw three tangents to the circle with centre at O at the three vertices of that triangle. |
Answer» Solution :Here O is the centre of the CIRCUMCIRCLE of `DeltaABC` . PQ, RS and UV are the three tangents to the circle at the vertices A, B and C RESPECTIVELY . 
|
|
| 1344. |
P divides segment QR internally in the ratio 2 : 1" " Q -= (-5, 8), R -= (4, -4) then P-=…. |
|
Answer» (0,1) |
|
| 1345. |
Construct a tangent to a circle of radius 3.7cm at any point . |
| Answer» | |
| 1346. |
Show that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment |
|
Answer» Solution :The proof will be taken up in two steps : Step 1: We, initially prove tha tany point equidistant form the end point of a line segment lies on the perpendicular bisector of the line segment. Given : M and N are two points on a plane. A is a point in the same plane such that `AM=AN`. RTP: A lies on the perpendicular bisector of MN. Proof : Let M and N be the two fixed points in a plane Let Abe a point such that `AM=AN` and L be the mid -points of `overline(MN)`. If A coincides with L, then A lies on the bisector of MN. Suppose A is different from L. Then, in `Delta MLA and Delta NLA`, `ML=NL,AM=AN` and AL is a common SIDE. `therefore` By SSS congruence property, `Delta MLA approx Delta NLA` `rArr ANGLE MLA =angle NLA(because "Corresponding elements of congruent triangles are equal") (1)` But `angle MLA +angle NLA =180^@(because "They form a straight angle")` `rArr 2 angle MLA =180^@("using(1))` `therefore angle MLA angle NLA =90^@` So, `overline(AL) bot overline (MN)` and hence `overline(AL)` is the perpendicular bisector of `overline(MN)`. `therefore` A lies on the perpendicular bisector of `overline(MN)`. Step 2 : Now, we prove that any point of the line segment. Given : MN is the segment and P is point on the perpendicular bisector. L is the mid-point of MN. RTP : `MP=NP` Proof : If P coincides with L, then MP=NP. Suppos Pis different from L. Then, in `Delta MLP and NLP, ML=LN` LP is the common side and `angle MLP=angle NLP=90^@` `therefore` By the SAS congruence property , `Delta MLPapprox Delta NLP`. So, `MP=PN` (`because` The corresponding bisector of `overline(MN)` is eqidistant from the points M and N . Hence , from the steps 1 and 2 of the proof it can be said that the locus of the point equidistant from two fixed points is the perpendicular bisector of the line segment joining the two points. 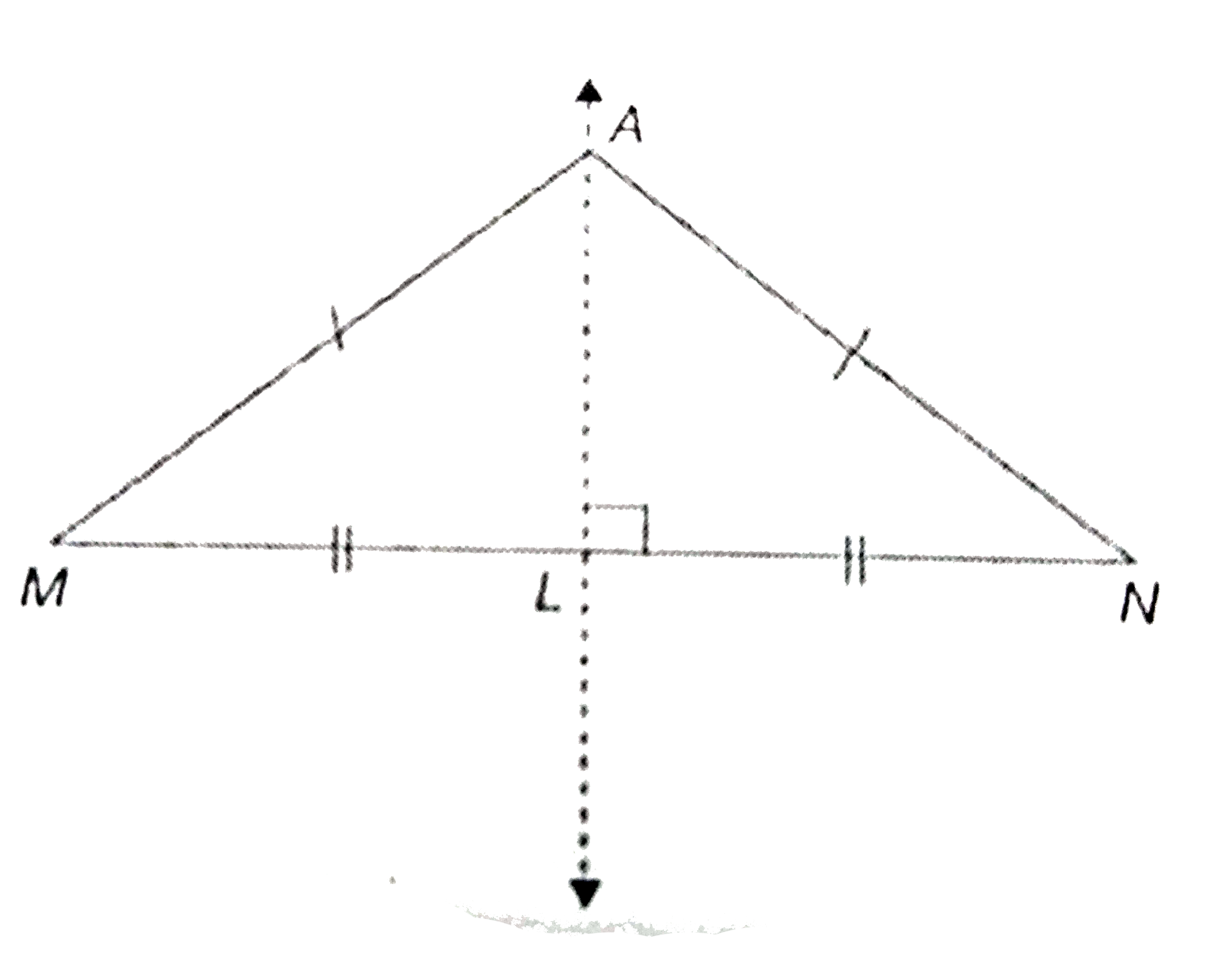 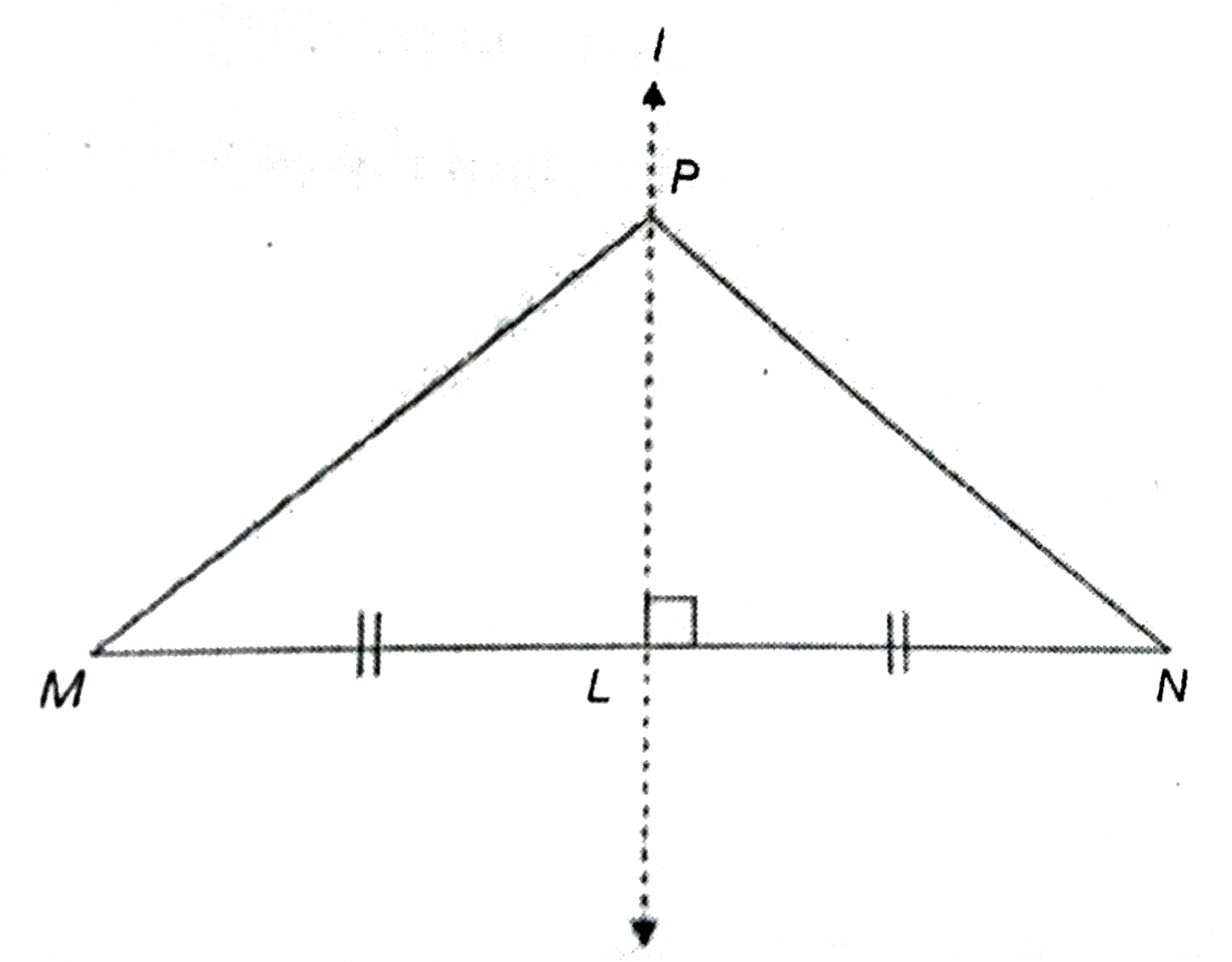
|
|
| 1347. |
Using ruler and compasses only construct a triangle ABC in which BC = 4 cm. angleACB = 45^(@) and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC |
|
Answer» |
|
| 1348. |
What do you mean by Euclid's divison lemma ? |
| Answer» | |
| 1349. |
Write down the coordinates of the point of intersection of the above equation. |
|
Answer» |
|
| 1350. |
B' is the image of B(3,2) when reflected in the y-axis . Write down the co-ordinates of B' . |
|
Answer» |
|