1.

In the previous question, if dv//dt = 0, then the angular acceleration of the ladder when alpha= 45^@ is.

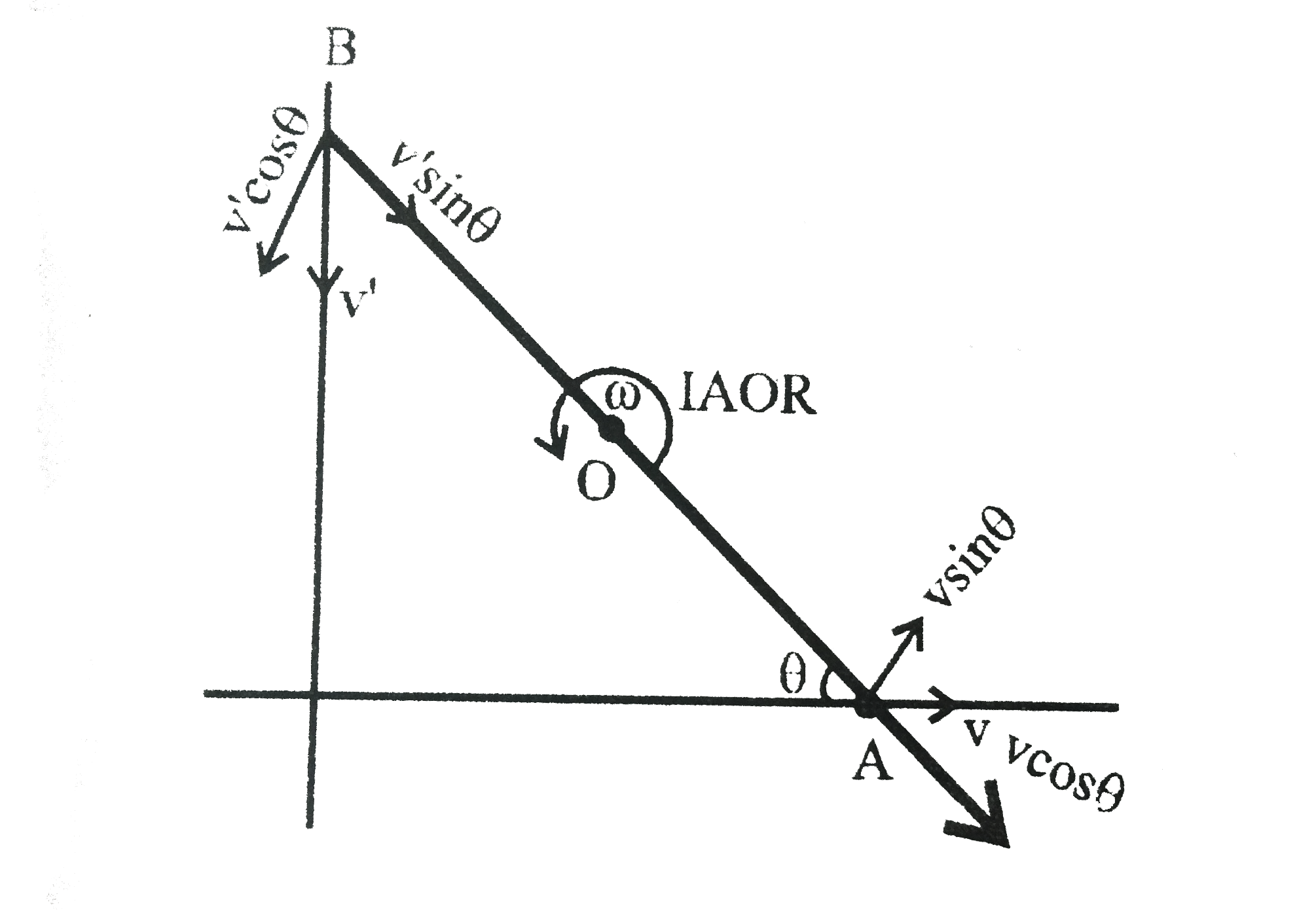Answer» <html><body><p>`2 <a href="https://interviewquestions.tuteehub.com/tag/v-722631" style="font-weight:bold;" target="_blank" title="Click to know more about V">V</a>^(2) L^(2)`<br/>`v^(2)//2L^(2)`<br/>`sqrt(2) [v^(2)//L^(2)]`<br/>None</p>Solution :<img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_MEC_V01_C03_E01_046_S01.png" width="80%"/> <br/> `v' sin theta = v cos theta`….(1) <br/> let <a href="https://interviewquestions.tuteehub.com/tag/instantaneous-516608" style="font-weight:bold;" target="_blank" title="Click to know more about INSTANTANEOUS">INSTANTANEOUS</a> axis of rotation is at distance `l` from <a href="https://interviewquestions.tuteehub.com/tag/end-971042" style="font-weight:bold;" target="_blank" title="Click to know more about END">END</a> `A`. <br/> `omega = (v sin theta)/(l) = (v' cos theta)/((L-l))` ....(2) <br/> from (1) &amp; (2) `omega = (v sin theta)/(l) = (v cos^(2) theta)/(sin theta (L - l))` <br/> `l = L sin^(2) theta`... (3) <br/> from (2) &amp; (3) <br/> `omega = (v cosec theta)/(L)` <br/> `(d omega)/(<a href="https://interviewquestions.tuteehub.com/tag/dt-960413" style="font-weight:bold;" target="_blank" title="Click to know more about DT">DT</a>) = (v)/(L) (-cos ec theta. cot theta) xx (d theta)/(dt)` <br/> `(d omega)/(dt) = (v)/(L) (-cos ec theta. cot theta) xx (v)/(L) cos ec theta` <br/> `<a href="https://interviewquestions.tuteehub.com/tag/alpha-858274" style="font-weight:bold;" target="_blank" title="Click to know more about ALPHA">ALPHA</a> = - (v^(2))/(L^(2))cos ec^(2) theta. cot theta` <br/> `alpha = - (v^(2))/(L^(2)) cos ec^(2) 45^@. cot 45^@ rArr alpha = -(2v^(2))/(L^(2))`.</body></html>


Discussion

No Comment Found

Related InterviewSolutions