1.

From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc andpassing through O is

Answer» <html><body><p>`4 MR^(2)`<br/>`40/9 MR^(2)`<br/>`40 MR^(2)`<br/>`37/9 MR^(2)`</p>Solution :<a href="https://interviewquestions.tuteehub.com/tag/mass-1088425" style="font-weight:bold;" target="_blank" title="Click to know more about MASS">MASS</a> per unit area of disc <br/> `=(9M)/(piR^(2))` <br/> Mass of <a href="https://interviewquestions.tuteehub.com/tag/removed-2986295" style="font-weight:bold;" target="_blank" title="Click to know more about REMOVED">REMOVED</a> portion of disc <br/> `=(9M)/(piR^(2)) xx pi(R/3)^(3) = M` <br/> <a href="https://interviewquestions.tuteehub.com/tag/moment-25786" style="font-weight:bold;" target="_blank" title="Click to know more about MOMENT">MOMENT</a> of <a href="https://interviewquestions.tuteehub.com/tag/inertia-1043176" style="font-weight:bold;" target="_blank" title="Click to know more about INERTIA">INERTIA</a> of removed portion about an <a href="https://interviewquestions.tuteehub.com/tag/axis-889931" style="font-weight:bold;" target="_blank" title="Click to know more about AXIS">AXIS</a> passing through center of disc and perpendicular to the plane of disc, using theorem of parallel axes is <br/> `I_(1)=M/2(R/3)^(2)+1/2(MR^(2))=4MR^(2)` 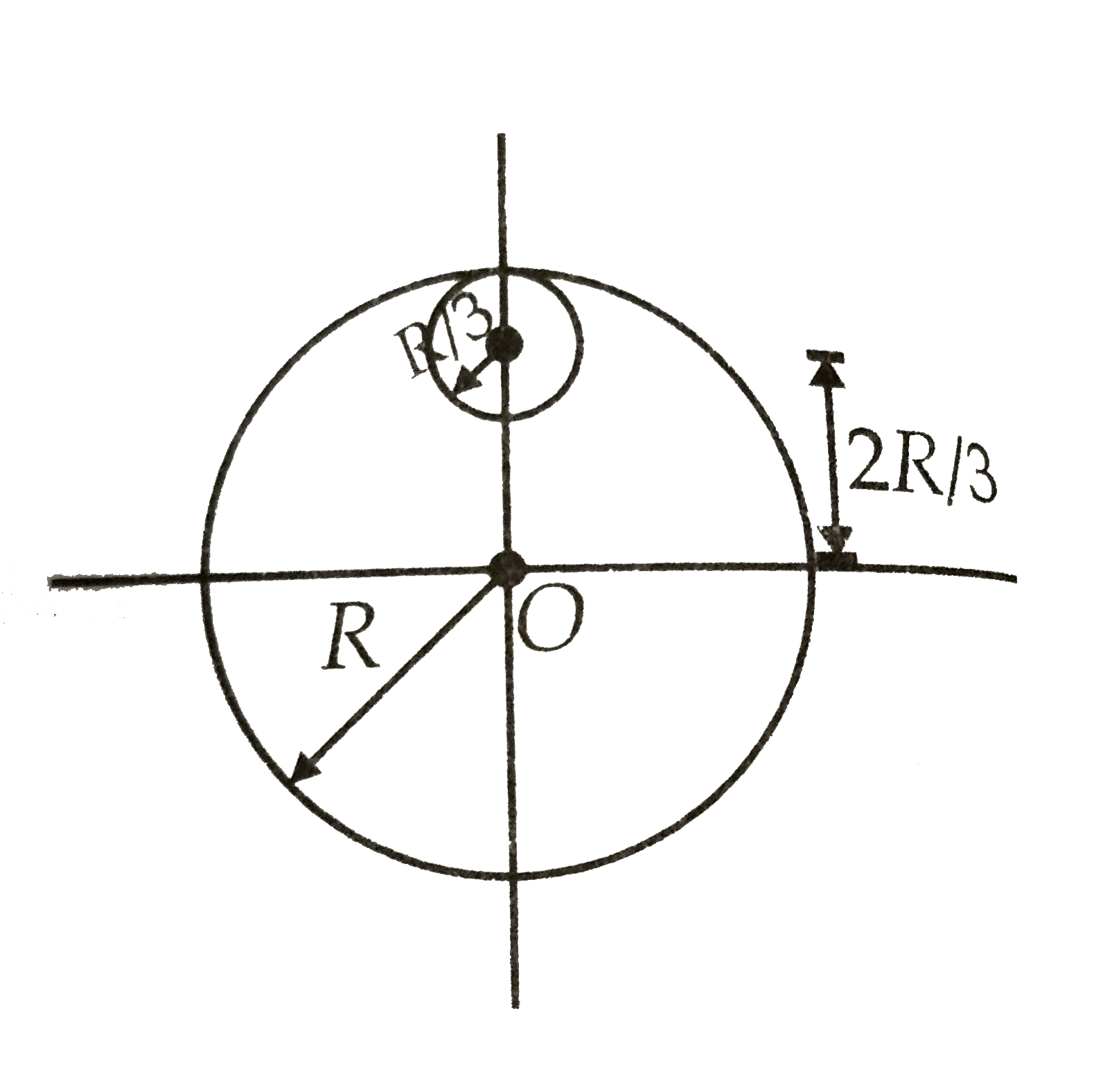<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_OBJ_FING_PHY_XI_C07_E01_052_S01.png" width="80%"/></body></html>


Discussion

No Comment Found

Related InterviewSolutions