Saved Bookmarks
| 1. |
Explain the meaning of diminishing marginal rate of substitution with the help of a numerical example. |
|
Answer» Solution :MRS is the rate at which a consumer is WILLING to sacrifice ONE commodity for an extra unity of another commodity without AFFECTING his total satisfaction. In other words, of `x_1` for `x_2(MRS_(x_1x_2))`will be the quantity of `x_1` which will just compensate the consumer for the loss of Marginal unity of `x_2 . "MRS"_(x_1x_2)` can be expressed as the ratio between the change in commodity `x_2(Deltax_2)` and change in commodity `x_1(Deltax_1)` without affecting the consumer level of satisfaction. Therefore, `MRS_(x_1,x_2)` can be expressed as, `MRS_(x_1.x_2)=("UNITS of "x_2 " willing to sacrifice")/("Units of "x_1 "willing to gain")=(Deltax_2)/(Deltax_1)` `MRS_(x_1x_2)` can also be written as, `MRS_(x_1,x_2) = ("Marginal Utility of "x_1[MU_(x_1)])/("Marginal Utility of "x_2[MU_(x_2)])""..(1)` As we KNOW, Change in `MU_(x_1)=("Total Utility")/("Change in Commodity "x_1)=(DeltaTU)/(Deltax_1)""...(2)` `MU_(x_2)=("Total Utility")/("Change in "x_2)=(DeltaTU)/(Deltax_2)""...(3)` commodity `x_2` Putting (2) and (3) in (1), `MRS_(x_1.x_2)=(Deltax_1)/((DeltaTU)/(Deltax_2))=(Deltax_2)/(Deltax_1)` So, `MRS_(x_1.x_2)=(Deltax_2)/(Deltax_1)=(MU_(x_1))/(MU_(x_2))` 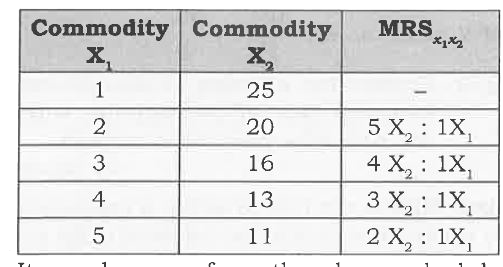 It can be seen from the above schedulethat the consumer substitute `X_1` for `X_2` but continues to get the same satisfaction. But for every increase of 1 unit of `X_1` , the consumer gives up lesser and lesser quantity of `X_2`. Therefore, this is called the law of diminishing marginal rate of substitution. |
|