Saved Bookmarks
| 1. |
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5. |
|
Answer» Solution :Steps of Construction : 1. DRAW a line segment AB = 7 cm. 2. Draw `AX"||"BY` such that `angleAand angleB` are acute angles. 3. Divide AX and BY in 3 and 5 parts equally by compass and mark `A_(1),A_(2),A_(3),B_(1),B_(2),B_(3),B_(4)and B_(5)` respectively. 4. Join `A_(3)B_(5)` which intersect AB at P and divides `AP: PB = 3:5.` Hence P is the REQUIRED point on AB which divide it in `3:5.` Verification (Justicicatio) : `In DeltaAA_(3)P and DeltaBB_(5)P` `""AX"||"BY""("by construction")` `""angleA=angleB""("alt.angles")` `""angleA_(3)PA=angleB_(5)PB""("vertically opp. angles")` `therefore""DeltaA A_(3)P~DeltaBB_(5)P""("by AA criterion of SIMILARITY")` `implies""(A A_(3))/(BB_(5))=(AP)/(BP)""("LET ecah equal part = c cm" thereforeA A_(1)=A_(1)A_(2)=B_(1)B_(2)...=x)` `implies""(3x)/(5x)=(AP)/(BP) implies""AP:BP=3:5` 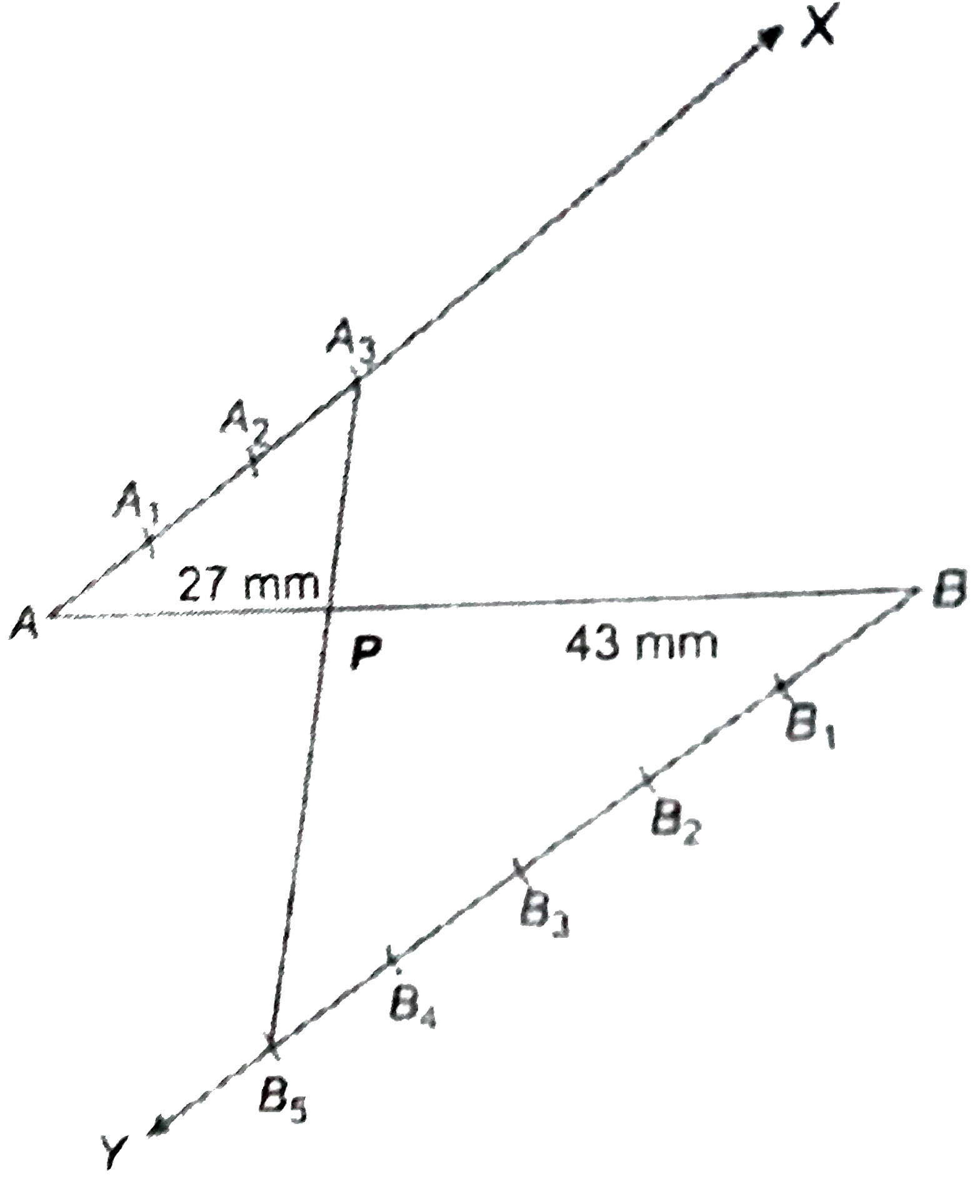
|
|
Discussion
No Comment Found
Related InterviewSolutions
- Find the sum of a] first 10 multiples of 8 b] first 25 multiples of 3 c] first 100 multiples of 2.
- Which of the following figures correctly represents the relation between:Doctors,Lawyers.Professionals?
- A solid metalli sphere of radius 6 cm is melted and made into a solid cylinder of height 32 cm. Find the : (i) radius of the cylinder (ii) curved surface area of the cylinder. (Take pi=3.1)
- Solve the following simultaneous equations : x/3 + y/4 = 2 , 3x + 4y = 25
- Construct a triangle similar to a given triangle ABC with its sides equal to (6)/(5) of the corresponding sides of the triangle ABC (scale factor (6)/(4)).
- A man has a choice to invest in hundread rupee shares of two firms at 120rs or at 132rs. The first firm pays a dividend of 5% per annum and the second firm pays a dividend of 6% per annum. Find : (i) which company is giving a better return. (ii) if a man invests 26400rs with each firm how much will be the difference between the annual returns from the two firms ?
- 10 students of Class-X took part in a mathematics quiz. If the number of girls in 4 more than the number of boys then, find the number of boys and the number of girls who took part in the quiz.\
- Number of distinct line segments that can be formed out of n- points is…
- Find the sum of the following Aps: (i) 2, 7, 12, …….., to 10 terms. (ii) -37, -33, -29, …….., to 12 terms. (iii) 0.6, 1.7, 2.8,….., to 100 terms (iv) (1)/(15), (1)/(12),(1)/(10),……,to 11 terms
- Write the following sets in the set-builder form (i) {3,6,9,12} (ii) {2,4,8,16,32} (iii) {5,25,125,625} (iv) {1,4,9,16,25,....,100}