1.

A balloon carrying a stone rises from rest on the ground with a constant acceleration 10 m//s^(2). After 5 s, the stone is released and ultimately it strikes the ground. Sketch a v-t graph for the stone and the maximum height attained by it.

Answer» <html><body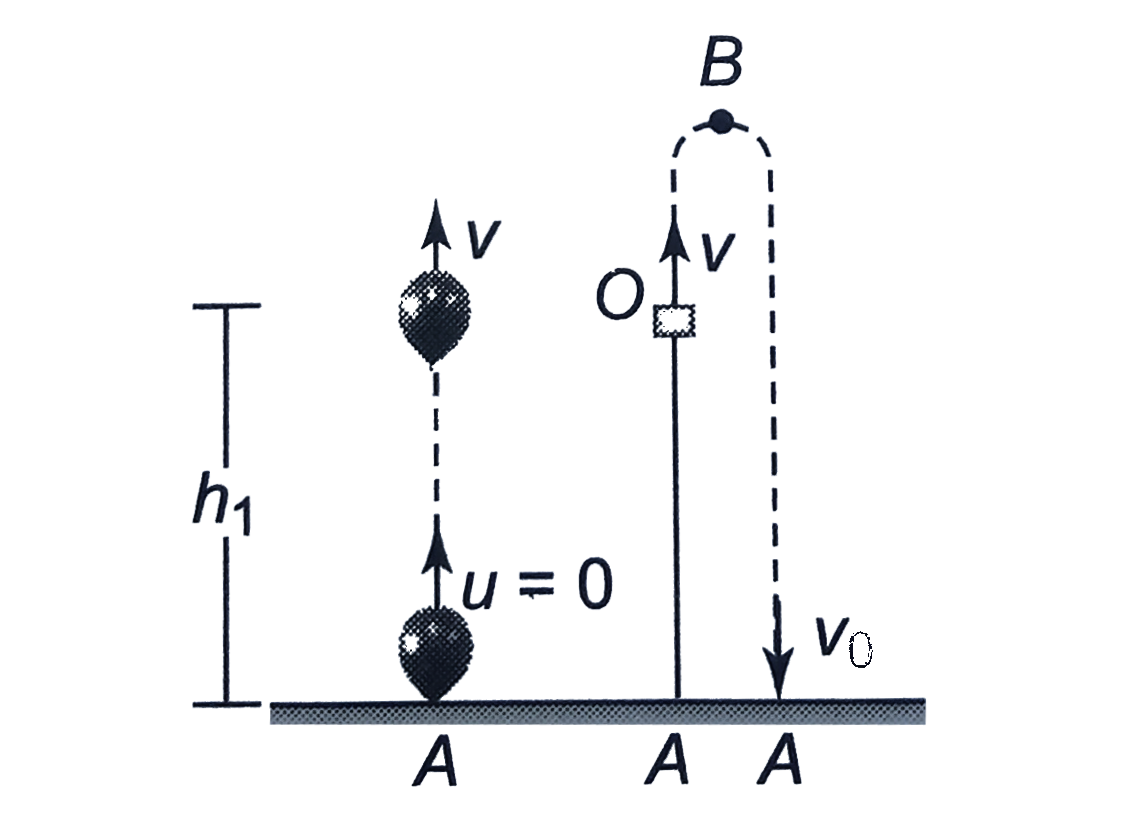><p></p>Solution :<img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V01_C02_S01_122_S01.png" width="80%"/> <br/> First the stone will accelerate with balloon. <br/> <a href="https://interviewquestions.tuteehub.com/tag/accelerated-366473" style="font-weight:bold;" target="_blank" title="Click to know more about ACCELERATED">ACCELERATED</a> motion: `t=0` to `t=5s` <br/> `v=u+a_(1)t=0+10t=50 m//s` <br/> `h_(1)=ut+1/2a_(1)t^(2)=0+1/2xx10xx5^(2)=<a href="https://interviewquestions.tuteehub.com/tag/125-271180" style="font-weight:bold;" target="_blank" title="Click to know more about 125">125</a> m` <br/> After release, the stone will move under gravity. <br/> Assuming O as the origin and upward direction +ve, O to A through B: <br/> Displacement`=-h_(1)=-125 m` <br/> `-h_(1)=v t_(2)-1/2g t_(2)^(2)` <br/> `-125=50t_(2)-<a href="https://interviewquestions.tuteehub.com/tag/5-319454" style="font-weight:bold;" target="_blank" title="Click to know more about 5">5</a> t_(2)^(2)` <br/> `t_(2)^(2)-10t-25=0` <br/> `t_(2)=(10+-sqrt(100+100))/2 =(10+-10sqrt(2))/2` <br/> `t_(2)=(10+-10xx1.4)/2 =12 s,-2s` <br/> The stone will strike the ground after 12 s (from its release). <br/> <a href="https://interviewquestions.tuteehub.com/tag/velocity-1444512" style="font-weight:bold;" target="_blank" title="Click to know more about VELOCITY">VELOCITY</a> of the stone at t=12 s, <br/> `v_(0)=v-g t_(2)=50-10xx12=-70 m//s` <br/> v-t graph for stone <br/> A to O: `t=0, v=0` <br/> `t=5 s, v=50 m//s` <br/> `v=10t` <br/> `y=10 x` (straight line) 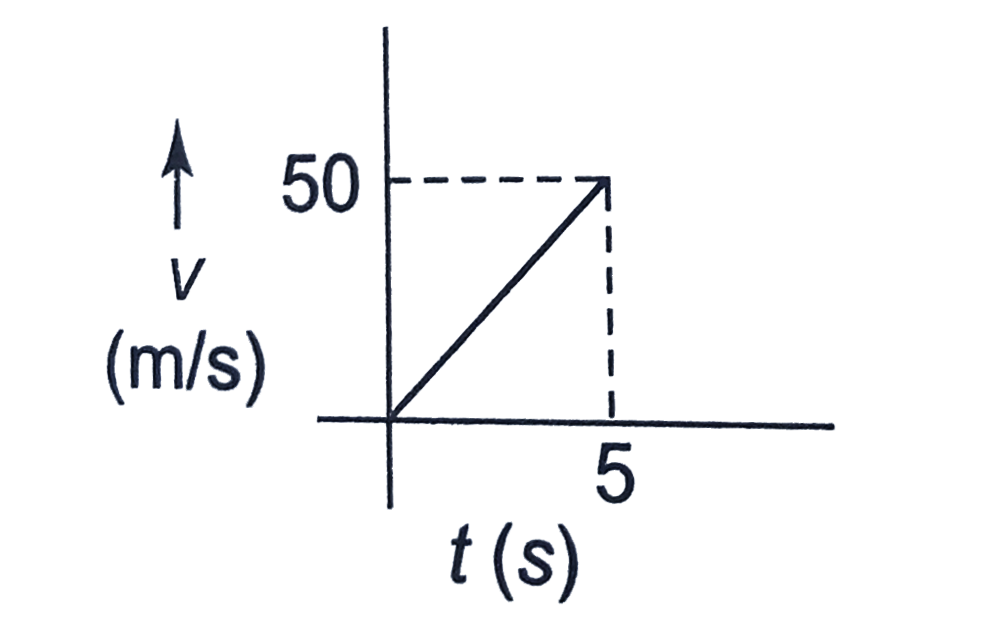<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V01_C02_S01_122_S02.png" width="80%"/> <br/> O to A through B: `v=50-10 t` <br/> `t=0, v=50 m//s` <br/> `t=12 s, v=-70 m//s` <br/> `v=0implies50-10timplies t=5 s` <br/> Shape: y=50-10x(straight line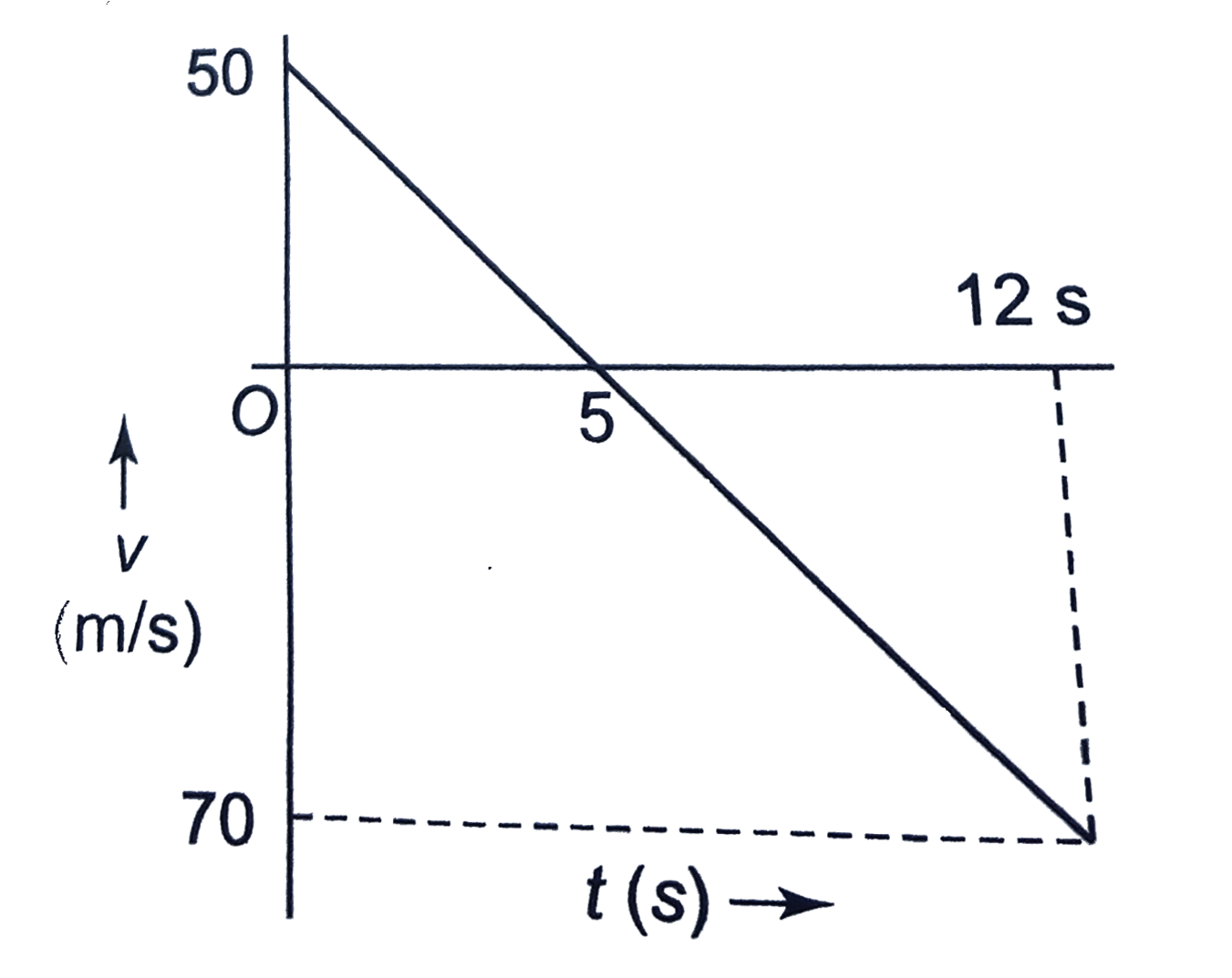) <br/> y=c+mx <br/> c=50, +ve <br/> m=-10, -ve <br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V01_C02_S01_122_S03.png" width="80%"/> <br/> Comdining the above two graph, we get the following graph: 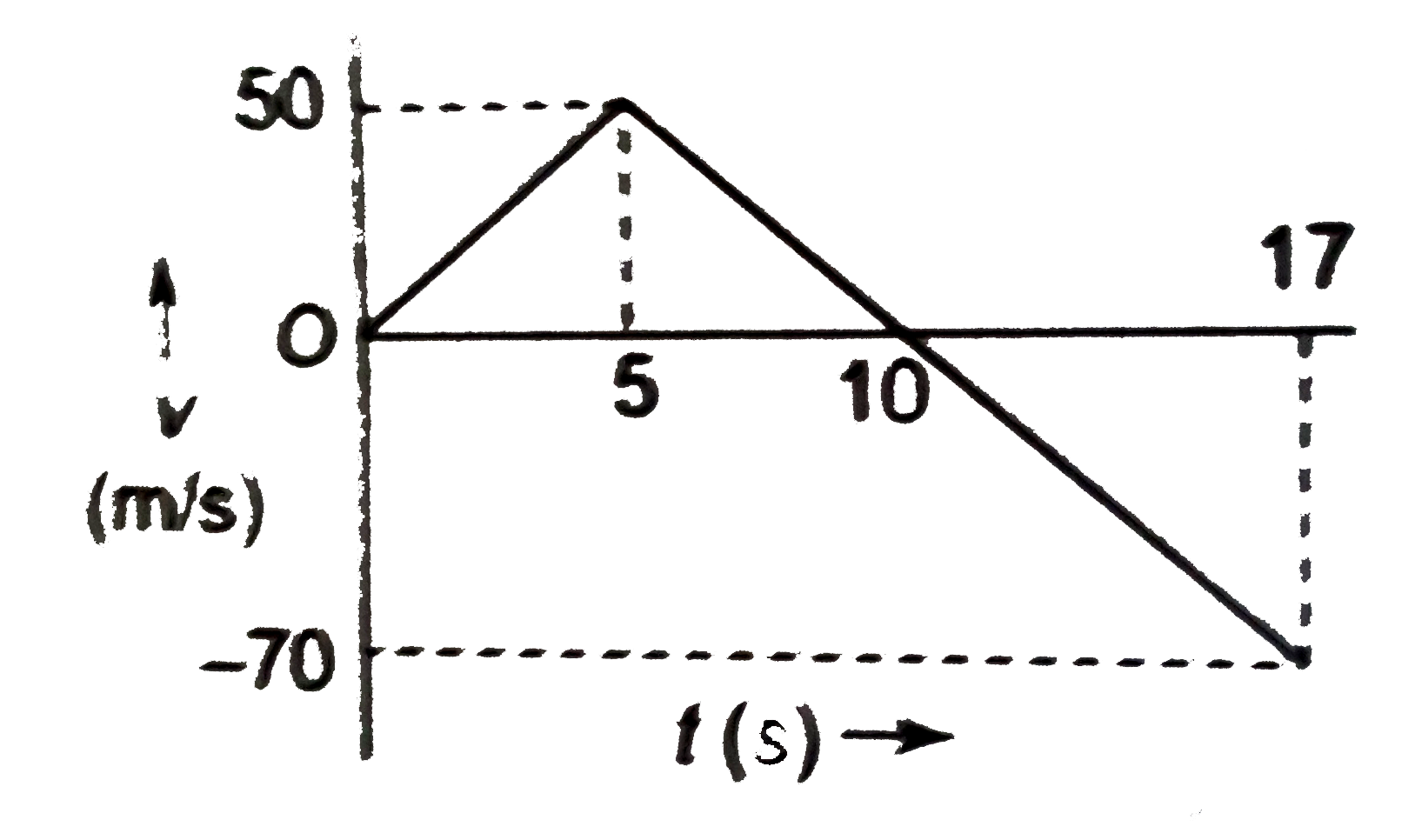<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V01_C02_S01_122_S04.png" width="80%"/> <br/> The area of the v-t graph from t=0 to t=10 s will give the maximum <a href="https://interviewquestions.tuteehub.com/tag/height-1017806" style="font-weight:bold;" target="_blank" title="Click to know more about HEIGHT">HEIGHT</a> attained by the stone. <br/> Maximum height`=1/2xx50xx10=250 m` <br/> OR <br/> If we take time from the start of the balloon, the velocity of the stone in terms of time after its release will be <br/> `v=50-10(t-5)=100-10t(5 s lt = t lt = 17 s)` <br/> `t=5 s, v=50 m//s` <br/> `t=17 s, v=-70 m//s` <br/> `v=0implies100-10T=0impliest=10 s` 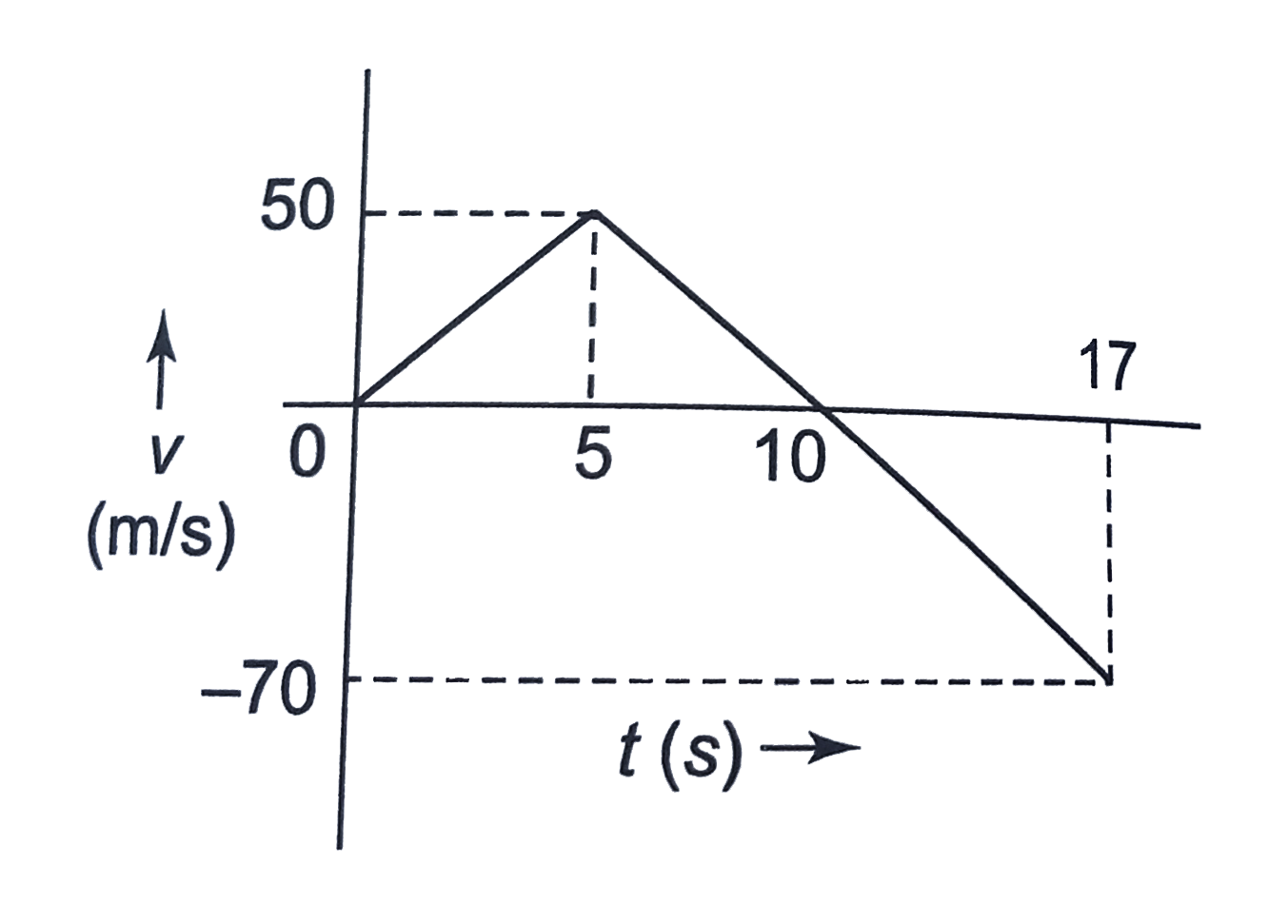<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V01_C02_S01_122_S05.png" width="80%"/></body></html>


Discussion

No Comment Found

Related InterviewSolutions